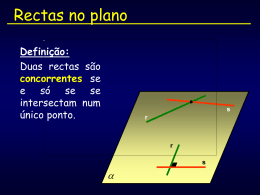
GEOMETRIA DESCRITIVA A
11.º Ano
Paralelismo entre Planos
© antónio de campos, 2009
O paralelismo entre dois planos ocorre quando
dois planos têm a mesma orientação. Dois planos
não paralelos têm orientações diferentes; são
secantes, intersectando-se numa recta.
Dois planos são paralelos entre si, se duas
rectas concorrentes de um plano forem
paralelas a duas rectas concorrentes de outro
plano.
Em geral (exceptuando os planos de rampa) os traços do plano (frontal e horizontal)
são duas rectas concorrentes do plano num ponto do eixo x.
Os planos α e δ (em baixo) são paralelos entre si, pois duas rectas concorrentes do
plano α (fα e hα) são paralelas a duas rectas concorrentes do plano δ (fδ e hδ).
Um plano oblíquo α definido pelos seus traços. Um ponto P exterior ao plano.
Para obter os traços de um plano δ, paralelo ao plano α , passando pelo ponto P.
A solução passa por conduzir pelo
ponto P, uma recta que pertença
ao plano δ. A opção é por recta
horizontal (de nível) h, como recta
auxiliar. Podia ter sido uma recta
frontal (de frente), paralela a fα.
Os traços de um plano oblíquo α são concorrentes num ponto com –2 de abcissa, que
fazem com o eixo x ângulos de 60º (a.d.) e 30º (a.e.), respectivamente em relação ao
fα e hα. Determina os traços de um plano δ, paralelo ao plano α e passando pelo ponto
P (3; 2; 3).
y≡ z
fα
fδ
h2
P2
x
F2
F1
hδ
h1
P1
hα
A solução passa pela utilização
de uma recta auxiliar horizontal
h, passando pelo ponto P, e
portanto pertencente ao plano δ.
Um plano α, vertical, corta o eixo x num ponto com –3 de abcissa, e faz um diedro de
60º (a.e.) com o Plano Frontal de Projecção. Determina os traços de um plano γ,
passando pelo ponto P (4; 2; 5) e paralelo ao plano α.
y≡ z
P2
fγ
fα
x
P1
hγ
hα
Por se tratar de planos
projectantes horizontais, basta
passar hγ por P1, pois um plano
projectante horizontal projecta
todas as suas rectas e pontos no
seu traço horizontal.
No caso dos planos de rampa, como os traços do plano (frontal e horizontal) não são
duas rectas concorrentes, é necessário estabelecer o paralelismo dos dois planos
entre si, através de uma recta de um plano e outra de outro plano. Se essas rectas
forem paralelas, então os planos também o são.
As duas rectas auxiliares a e b, utilizadas para determinar o paralelismo dos dois
planos, não são paralelas, o que significa que os dois planos não são paralelos.
Pretendem-se os traços de um plano σ, que é paralelo a um plano ρ, de rampa, e
contém o ponto P.
Mais uma vez, o recurso de
rectas dos planos para
ajudar a determinar o
paralelismo entre os planos.
A partir da recta r do plano
ρ, obtem-se os traços
paralelos da recta s, para
depois obter os pontos H e P
para definir os traços do
plano de rampa σ.
Os traços frontal e horizontal do plano de rampa ρ, têm, respectivamente, 2 cm de
cota e 3 cm de afastamento. Os traços frontal e horizontal do plano de rampa σ,
têm, respectivamente, 4 cm de cota e 6 cm de afastamento. Determina se os dois
planos de rampa são paralelos entre si.
fσ
F’2
s2
fρ
F2
H’2
H2
x
F1
r2
hρ
r1
H1
s1
hσ
H’1
F’1
Um plano passante σ, definido pelo eixo x e por um ponto P (2; 5; 3) é paralelo a um
plano de rampa ρ, plano que contém o ponto A (-3; 4; 5). Determina os traços do
plano ρ.
f
ρ
y≡ z
A2
r2
s2
P2
F2
x ≡ fσ ≡ hσ
F1
s1
r1
h
ρ
H1
A solução passa pela utilização
de uma recta auxiliar passante r,
passando pelo ponto P, e
portanto pertencente ao plano σ.
P1
A1
H2