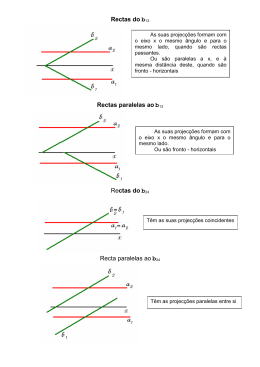
GEOMETRIA DESCRITIVA A
11.º Ano
Paralelismo entre Rectas
© antónio de campos, 2009
No espaço, duas rectas são paralelas se são
complanares (estritamente paralelas) e não têm
nenhum ponto em comum, ou se são rectas
coincidentes.
O presente estudo debruça-se sobre todas as
situações de paralelismo estrito entre rectas.
As rectas a e b são
paralelas entre si no
espaço.
As suas projecções
horizontais a1 e b1
são paralelas entre si.
As suas projecções
frontais a2 e b2 são
paralelas entre si.
Em geral é assim.
Com as rectas de perfil, não basta verificar se as projecções frontais e horizontais
são paralelas, é necessário confirmar, por exemplo, com rectas auxiliares. Em baixo,
duas rectas de perfil que não são paralelas, apesar das suas projecções frontais e
horizontais serem paralelas.
Neste exemplo, duas
rectas auxiliares r e s
são paralelas, pelo que
são complanares.
Assim sendo, as
rectas p e p’ são
complanares, e como
não são concorrentes,
são paralelas.
Neste exemplo, duas rectas
auxiliares r e s não são paralelas,
mas são complanares com as
rectas p e p’. Assim sendo, as
rectas p e p’ são complanares, e
como não são concorrentes, são
paralelas.
A recta de perfil p está definida pelos pontos A (1; 1; 5) e B (4; 2). A recta de
perfil p’ está definida pelos pontos C (-3; 4; 3) e D (1; 4). Averigúa a posição
relativa das duas rectas.
y≡ z
p1 ≡ p2
p’1 ≡p’2
r2
A2
B2
D2
C2
s2
x
r1
A1
D1
B1
C1
s1
Sobre a posição relativa
das duas rectas, sabe-se
imediatamente que não são
concorrentes – podem ser
paralelas ou enviesadas.
y≡ z
Se forem paralelas, então
são complanares, pelo que
quaisquer duas rectas
concorrentes com p e p’
serão, também elas,
complanares.
Recorreu-se a duas rectas
auxiliares, as rectas r e s.
A recta r é concorrente
com p em A e com p' em D
(está definida por dois
pontos). A recta s é
concorrente com p em B e
com p' em C (está
definida por dois pontos).
As rectas r e s não são
complanares (não são
paralelas nem
concorrentes), pelo que p e
p' não são complanares –
logo, não são paralelas.
p’1 ≡ p’2
p1 ≡ p2
r2
A2
B2
D2
C2
s2
x
r1
A1
D1
B1
C1
s1
A mesma recta de perfil p definida pelos pontos A (1; 1; 5) e B (4; 2). Desenha
as projecções de uma recta de perfil p’, paralela à recta p e passando pelo
ponto M (-2; 3; 4).
y≡ z
p’1 ≡ p’2
p1 ≡ p2
r2
A2
s2
M2
r1
B2
N2
x
A recta auxiliar s paralela à
recta r (derivada dos pontos
A e M conhecidos e
concorrentes com p e p’)
localiza o ponto N, definindo
a recta de perfil p’ paralela à
recta de perfil p.
s1
A1
M1
B1
N1
Averigúa se as rectas de perfil p e p’ são ou não paralelas. Ambas as rectas
estão contidas no plano de perfil π. A recta p está definida pelos pontos E (3;
1) e F (1; 2). A recta p’ está definida pelos pontos M (6; 2) e N (4; 3).
p1 ≡ p2 ≡ p’1 ≡ p’2 ≡ fπ ≡ hπ ≡ e2 ≡
fπr
p’r
pr
Nr
N2
F2 ≡ M2
E2
x ≡ hπr
Mr
Fr
Er
(e1)
F1
E1
N1
M1
Utilizou-se o rebatimento
para o Plano Frontal de
Projecção, obtendo-se a
recta pr e p’r, que são
paralelas, e por tanto as
rectas p e p’ são também
necessariamente paralelas.