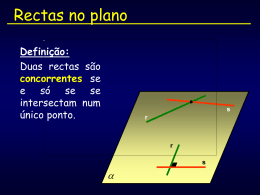
Posição relativa de
rectas e planos
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Noção de Plano
Se prolongares indefinidamente e em todas
as direcções o tampo do quadro, obténs um
Plano.
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Como desenhar um plano é impossível, os
matemáticos decidiram que este seria
representado por um
A

B
C
e designá-lo por uma letra grega
ou por três dos seus pontos não colineares.
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Posição relativa de planos
Se dois planos distintos se intersectarem
dizemos que são Concorrentes e a sua
intersecção é sempre uma recta.
Os planos α e  são
concorrentes.
Exercício: dá exemplos de planos concorrentes na sala
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Paralelos
Se dois planos não tiverem nenhum ponto em
comum dizemos que são Estritamente
Paralelos.
Os planos α e  são
estritamente paralelos.
Se dois planos coincidirem em todos os pontos
dizemos que são Coincidentes .
Os planos α e  são
coincidentes.
Exercício: dá exemplos de planos paralelos na sala
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Exercício: Considera os planos que correspondem
ao prolongamento das faces do sólido e completa a
seguinte tabela.
Planos paralelos
Planos concorrentes
ADC e EHG
AEF e BGH
ABG e CDE
ABC e ABG
CDE e CBH
BGH e HEF
D
A
C
B
E
F
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
H
G
2006/2007
Posição relativa de rectas e
planos
Dizemos que uma recta é Concorrente a um
plano se tem um único ponto em comum com
esse plano.
A recta r é concorrente
ao plano α.
Dizemos que uma recta é Estritamente
Paralela a um plano se não tem nenhum
ponto em comum com esse plano.
A recta r é estritamente
paralela ao plano α.
Se todos os pontos de uma recta pertencerem ao
plano dizemos que esta está Contida no plano.
A recta r está contida
(ou aposta) no plano α.
Exercício: dá exemplos de rectas paralelas a planos
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Exercício: Considera as rectas que correspondem
ao prolongamento das arestas do sólido e
completa a seguinte tabela.
Rectas paralelas a planos
Recta AB e plano EFG
Recta BG e plano CDE
Recta DE e plano DEF
Rectas concorrentes a planos
Recta AD e plano CDE
Recta DE e plano ABC
Recta DB e plano ABG
D
A
C
B
E
F
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
H
G
2006/2007
Posição relativa de rectas
Dizemos que duas rectas são Não
Complanares se não há nenhum plano que as
contenha simultaneamente.
As duas rectas são não
complanares.
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Dizemos que duas rectas são Complanares
se existir um plano que as contenha
simultaneamente.
As três rectas são
complanares.
Exercício: dá exemplos de rectas complanares
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Se duas rectas se intersectarem num único
ponto dizemos que são Concorrentes.
As rectas a e b são
concorrentes.
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Paralelas
Se duas rectas não tiverem nenhum ponto
em comum dizemos que são Estritamente
Paralelas.
As rectas a e b são
estritamente paralelas.
Se duas rectas coincidirem em todos os pontos
dizemos que são Coincidentes.
As rectas a e b são
coincidentes.
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007
Exercício: Considera as rectas que correspondem
ao prolongamento das arestas do sólido e
completa a seguinte tabela.
Rectas não
complanares
Rectas paralelas
Rectas
concorrentes
FG e CH
AB e DE
AF e EH
AB e DC
BG e CH
AD e GH
AD e AB
AC e CB
EF e EH
D
A
C
B
E
F
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
H
G
2006/2007
FIM
Adaptado por Núcleo de Estágio de Matemática
Alcino Simões, Carina Jegundo, Catarina Pratas e Susana Costa
2006/2007