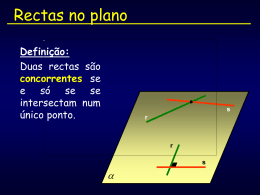
Geometria no Espaço I
(10º - Ano)
10º Ano
Rectas e planos
1. Dois pontos distintos do plano ou do espaço definem uma e
uma só recta
2. Três pontos distintos do espaço, não colineares, definem um
plano ( e se forem colineares?)
3. Qualquer recta com 2 pontos num plano está contida nesse
plano
4. Se dois planos distintos têm um ponto comum, a sua
intersecção é uma recta
5. Por um ponto exterior a uma recta passa uma e uma só
paralela a essa recta
10º Ano
Modos de definir um plano
Um plano fica definido por:
• Três pontos distintos, não colineares
• Um ponto e uma recta que não o contenha
• Duas rectas paralelas mas não coincidentes
• Duas rectas concorrentes
10º Ano
Posição entre
Rectas
10º Ano
Definição
Paralelismo:
No espaço duas rectas são
paralelas se satisfazem as
seguintes condições:
- são complanares
- não têm nenhum ponto comum,
ou
são coincidentes
10º Ano
Definição
Perpendicularidade:
No espaço duas rectas são
perpendiculares se, por um ponto
qualquer, é possível traçar duas
rectas perpendiculares, paralelas às
duas rectas dadas.
10º Ano
D ef inição de perpendicularidade ent re rec tas:
2 rect as são _| _s se por um pont o qualquer (B) f or
pos sí v el t raçar 2 rec tas _| _s (BC_| _BA) paralelas às
rec tas dadas ( BC/ / FG e BA/ /D C)
D
A
C
B
H
10º Ano
E
G
F
Propriedades de:
paralelismo
e
perpendicularidade:
10º Ano
1- Duas rectas paralelas
(//s) a uma terceira, são
paralelas entre si.
10º Ano
2 rectas paralelas a uma terceira são paralelas entre si
DC // EF porque
DC // AB
EF // AB
D
C
A
B
H
E
10º Ano
G
F
2- Dadas duas rectas
paralelas, todo o plano
que
intersecta
uma,
intersecta a outra.
10º Ano
Dadas 2 rectas paralelas, todo o plano que intersecta uma intersecta outra
DC // EF o plano BCGF
intersecta DC em C e EF
em F
D
C
A
B
H
E
10º Ano
G
F
3 - Se duas rectas são _|_s,
toda a recta paralela a uma
é _|_ à outra.
10º Ano
Se 2 rectas são _|_ s, toda a recta paralela a uma é _|_ à outra
D
DC_|_ FG , então
C
A
B
HG // DC e HG_|_FG
ou
BC // FG e BC _|_DC
H
E
10º Ano
G
F
4 - Se duas rectas são //s,
toda a recta _|_ a uma
é _|_ à outra
10º Ano
Se 2 rectas são paralelas, todo a recta _|_ a uma é _|_ à outra
DC // EF então
BC _|_ DC e BC _|_ EF
D
C
A
B
H
E
10º Ano
G
F
Posição entre
Rectas
e
Planos
10º Ano
Definição
Paralelismo:
Uma recta é paralela a um
plano se não é secante ao
plano
10º Ano
Definição
Perpendicularidade:
Uma recta é
perpendicular a um
plano se é perpendicular
a todas as rectas do
plano.
10º Ano
Definição de per pendicularidade entre recta e plano:
1 recta é _|_ a um plano se é _|_ a todas as rectas do
plano
DC _|_ ao plano BCGF pq
é _|_ a todas rec tas do
plano (CG, FG,FB e BC)
D
A
C
B
H
E
10º Ano
G
F
Propriedades:
10º Ano
1- Critério de paralelismo
entre recta e plano:
Se existir, num plano, uma
recta paralela a uma recta
dada, que não está contida
nesse plano, a recta e o
plano são paralelos
10º Ano
Critério de paralelismo entre recta e plano:
Uma recta exterior a um plano é paralela a esse plano, se for paralela a
uma recta contida no plano
AD não pertence ao plano BCF
mas BC // AD, logo AD// BCF
D
C
A
B
H
E
10º Ano
G
F
2- Dadas duas rectas não
complanares, existe um e
um só plano que contém
uma e é paralelo à outra
10º Ano
Dadas duas rectas não complanares, existe um e um só plano
que contém uma e é paralelo à outra
AD e CG são não complanares,
existe o plano BCF que contém
CG e é // AD
D
C
A
B
H
E
10º Ano
G
F
3- Critério de perpendicularidade
entre recta e plano:
Se uma recta é
perpendicular a duas rectas
concorrentes de um plano,
então a recta é
perpendicular ao plano.
10º Ano
Critério de perpendicularidade entre recta e plano:
Se uma recta é _|_ a duas rectas concorrentes de um plano,
então a recta é _|_ ao plano
Se DC _|_CG e DC_|_BC
então DC _|_BCGF
D
C
A
B
H
E
10º Ano
G
F
Posição entre
Planos
10º Ano
Definição
Paralelismo:
Dois planos são
paralelos se não são
secantes
10º Ano
Definição
Perpendicularidade:
Dois planos a e b são
perpendiculares se em a existe
uma recta perpendicular a b
e se em b existe uma recta
perpendicular a a
10º Ano
Definição de perpendicularidade entre dois planos:
Dois planos são _|_s se em cada um deles existir uma
recta _|_ ao outro plano
ABD _|_ BCF porque
DC _|_ BCF e BF_|_ABD
D
A
C
B
H
E
10º Ano
G
F
Propriedades:
10º Ano
1 - Critério de paralelismo
entre planos:
Se duas rectas
concorrentes de um
plano são paralelas a
outro plano, então os
planos são paralelos
10º Ano
2- Existe um só plano que
passa por um ponto dado e
é paralelo a um plano dado
10º Ano
Critério de paralelismo entre planos:
Se duas rectas concorrentes de um plano são //s a outro plano,
então os planos são //s.
Se AD e DC são concorrentes e //s a EFGH
então ABCD//EFGH
D
C
A
B
H
E
10º Ano
G
F
Existe um só plano que passa por um ponto dado e
é paralelo a um plano dado.
Pelo ponto dado D só passa o plano ADE
que é paralelo ao plano BCF
D
C
A
B
H
E
10º Ano
G
F
3- Se um plano intersecta
dois planos, as rectas de
intersecção são paralelas
10º Ano
Se um plano (amarelo) intersecta dois planos
paralelos (azuis) então as rectas de intersecção
são paralelas.
D
C
A
B
H
E
10º Ano
G
F
4- Critério de perpendicularidade
entre planos:
Se num plano existe uma
recta perpendicular a outro
plano, então os dois planos
são perpendiculares
10º Ano
Critério de perpendicularidade entre planos:
Se num plano existe uma recta _|_ a outro plano,
então os planos são _|_ s .
Se D C _| _CG e D C _| _BC
ent ão D C _|_BCGF, logo
o plano ABC D_|_BC GF
D
C
A
B
H
E
10º Ano
G
F
É Tudo!!!
10º Ano