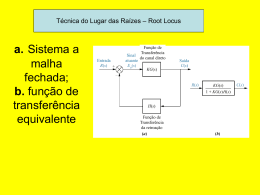
Técnica do Lugar das Raízes – Root Locus
a. Sistema a
malha
fechada;
b. função de
transferência
equivalente
Entrada
Função de
Transferência
Sinal
do canal direto
atuante
Função de
Transferência
da retroação
Saída
Pólos e Zeros da F.T.M.F. em função
dos pólos e zeros da F.T.M.A
N G s 
N H s 
G s  
; H s  
DG s 
DH s 
N G s 
K
DG s 
KN G s DH s 
T s  

N G s  N H s  DG s DH s   KN G s N H s 
1 K
DG s  DH s 
Os Zeros de T(s) são os zeros de G(s) e os pólos de
H(s), mas os pólos de T(s) não podem ser
determinados diretamente, eles precisam ser
calculados e mais do que isto, dependem do valor de K
Exemplo
• Calcule os pólos e zeros para a F.T.M.F.
quando G(s) e H(s) são dadas por:

s  1
Gs  
ss  2
;

s  3
H s  
s  4
Os Zeros valem: -1 e -4
Os pólos serão dados pelas raízes do polinômio abaixo que
dependem de K.
s 3  6  K s 2  8  K s  3K
Representação
vetorial de
números
complexos:
a. s =  + j;
b. (s + a);
c. representação
alternativa de
(s + a);
d. (s + 7)|s5 + j2
Plano s
Plano s
Plano s
Plano s
m
F s  
 s  z 
i
i 1
n
 s  p 
produtodos fatores com plexosdo num erador
produtodos fatores com plexosdo denomin ador

j
j 1
m = número de zeros ; n = número de pólos
Como F(s) é um número complexo ele pode ser representado através
da forma polar ou seja, por um MÓDULO e uma FASE :
M

m
M 
 com prim ento dos vetores correspondentes aos zeros

 s  z 
i
i 1
n
 com prim ento dos vetores correspondentes aos pólos  s  p 
i
j 1
   angulosdos zeros 

 s  zi 
m
i 1
n
-

j 1
 angulodos pólos
s  p 
j
Exemplo
G s  
s 1
s2
s 1
G s  
s2
considereo mapeamentopara s  1  j , ou seja :
s  1 j
1 j 1
j
j 1  j 
1 j 1 1




  j
 1  j  2 1  j 1  j 1  j 
2
2 2
2
2
2
1 1
cujo módulo vale:      
2
2 2
e a fase vale: tg
1
1
2    45o
1
4
2
j
j
L2
x
2
2
L1
o
1
1

L1  1
L2  12  12  2
L1
1
2
Módulo igual a


L2
2
2
1  90o
1
1
Fase igual a 1   2  90o  45o  45o
 2  tg 1  45o
Representação
vetorial da
equação:
s 1
F s  
ss  2 s  3 j 4
zero em  1  módulo 20 e fase  116,60
pólo em zero  módulo 5 e fase  126,90
pólo em  2  módulo 17 e fase  104,00
Módulo 0,217 ; Fase  114,30
Cortesia de ParkerVision.
a. Sistema que
rastreia
automaticamente
objetos;
b. diagrama de
blocos;
c. função de
transferência a
malha fechada
Tabela 8.1
Localização dos pólos como função do ganho
do sistema mostrado anteriormente
s 2 10s  K
a. Diagrama de
pólos com base
na tabela 8.1;
b. lugar das
raízes
FUNDAMENTO GERAL DO LUGAR
DAS RAÍZES – PÓLOS DE MALHA
FECHADA
KG s 
T s  
1  KG s H s 
Raízes do denominador, qualquer valor de " s"
tal que 1  KG s H s   0
ou KG s H s   1  KG s H s   1 e
fase de KG s H s   2n  1180 n  0,  1,  2,....
o
Veja exemplo para o sistema de câmara apresentado anteriormente para
por exemplo o pólo em -1 que acontecerá para um ganho k=9
a. Sistema
de Exemplo;
b. diagrama
de pólos e
zeros de
G(s)
Verifique se os pontos “s”
abaixo são pólos do sistema
de malha fechada
s  2  j3
2
e s  2  j
2
Plano s
Representação vetorial
de G(s) com base na
Fig. 8.6(a) em –2+ j 3
Plano s
1  56,31o
 2  71,57o
 3  90o
 4  108,43o
1  2  3  4  70,55o
NÃO PERTENCE AO LUGAR DAS RAÍZES
2
s  2  j
2
j
  19,471o
 2  35,264o
3  90o
 4  144,736
o
1  2 3 4  180,00o
L1  2,12 ; L2  1,22 ; L3 
LL
2
; L4  1,22 ; K  3 4  0,33
2
L1L2
PERTENCE AO LUGAR DAS RAÍZES
2
2