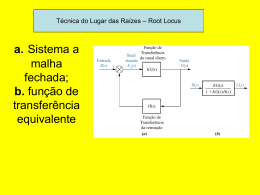
Sistemas lineares
discretos e amostrados
Texto base: Alexandre Tofino
Apresentação: Nestor Roqueiro
DAS/CTC/UFSC
Introdução
• Processos contínuos controladores
discretos
• Período de amostragem (teorema de
Shanon)
• Diagrama de sistema continuo com
controlador discreto
• Considerações praticas
Representação de estados
Modelo em tempo discreto
onde x(kT); u(kT); y(kT) é o estado, controle e saída
no instante t = kT. A primeira equação indica como o
estado é calculado a partir do estado e controle no
instante atual gerando assim uma recursividade na
atualização do estado
Discretização das
equações de estado
Considerando as equações de tempo contínuo
cuja solução é:
Vamos assumir que o controle é constante entre os
instantes de amostragem.
Discretização das
equações de estado
• Como todas as componentes do sinal u(t) são
constantes nos intervalos kT a kT + T tem-se:
• Multiplicando por eAT e subtraindo
Discretização das
equações de estado
• Como u(t) é constante no intervalo kT - kT +T
podemos substituir a constante u( ) por u(kT) e
mudar a variável (t =  + kT)
• Definindo
•
tem-se
Propriedades
estruturais
• Controlabilidade: Um sistema discreto
de dimensão n é controlável se for
possível, por meio de um vetor de
controle, constante nos intervalos de
amostragem e sem restrições de
magnitude, transferir o sistema de
qualquer estado inicial x(kT) para
qualquer outro estado desejado num
intervalo de n períodos de amostragem.
Propriedades
estruturais
Pode-se construir um teste para a controlabilidade do
sistema a partir da a solução da equação recursiva:
obtendo-se:
Como os estados x(0) e x(nT) são arbitrários a matriz
deve ter posto n.
Logo, posto(Mc) = n é a condição (necessária e suficiente)
para que um sistema seja controlável.
Propriedades
estruturais
• Quando a matriz de controlabilidade possui posto r,
inferior ao número de variáveis de estado, então existe
uma transformação de similaridade T unitária (T’ =T-1) tal
que:
onde os autovalores de Anc são os autovalores não
controláveis do sistema (se existir algum), o par (Ac;Bc) é
controlável e a seguinte igualdade se verifca:
• A função de transferência do sistema não se altera se
descartamos os estados não controláveis
Propriedades
estruturais
• Estabilizabilidade: O sistema é dito ser
estabilizável quando os autovalores não
controláveis são estáveis, isto é os
autovalores de Anc possuem módulo inferior à
unidade.
• Observabilidade: O sistema é observável se
todo estado inicial x(0) puder ser
determinado a partir do conhecimento de
y(kT); u(kT) durante um intervalo de tempo
finito.
Propriedades
estruturais
• Da definição podemos construir um teste para a
observabilidade de um sistema. Para uma dada
condição inicial x(0) e um sinal de controle
conhecido u(kT), a resposta do sistema é:
• Com as n primeiras medidas efetuadas temos
as relações:
Propriedades
estruturais
• Com as n primeiras medidas efetuadas temos as
relações:
• Como o lado esquerdo das igualdades acima são
valores conhecidos (medidas e controle) poderemos
encontrar x(0) a partir dessas expressões
Propriedades
estruturais
• Isto será possível quando a matriz
conhecida como matriz de observabilidade, possuir posto
igual ao número de variáveis de estado. Por outro lado,
quando posto(Mo) é inferior ao número de variáveis de
estado existe uma condição inicial x(0) tal que Mox(0) = 0.
Logo, para essa condição inicial teremos o lado direito de
todas as expressões nulo e nesse caso a condição inicial
desaparece das expressões indicando que não será
possível recuperá-la e o sistema não é observável.
Propriedades
estruturais
• Quando a matriz de observabilidade possui posto r,
inferior ao número de variáveis de estado, então existe
uma transformação de similaridade T unitária (T’ =T-1)
tal que:
onde Ano contém os autovalores não observáveis (se
existir algum), o par (Ao;Co) é observável e a seguinte
igualdade se verifca:
A função de transferência do sistema não se altera se
descartamos os estados não observáveis.
Propriedades
estruturais
• Detectabilidade: O sistema é dito ser
detectável quando os autovalores não
observáveis são estáveis, isto á os
autovalores de Ano possuem módulo
inferior à unidade.
Realização de estados
• A obtenção de uma representação de estados
do sistema a partir da sua função de
transferência recebe o nome de realização de
estados.
• Para sistemas SISO existem procedimentos
bastante simples de realização de estados.
• Por exemplo, dado a função de transferência
Realização de estados
• Com a introdução de uma variável intermediária
R(z)
Sendo y(t)[n] = y(kT + nT) o deslocamento
temporal de n passos à frente da variável y(t) no
instante t = kT e lembrando que as condições
iniciais são nulas nas equações acima, usando
a transformada inversa podemos reescrevê-las:
Realização de estados
• Escolhendo como variáveis de estado
Até i = q - 1, temos as seguintes relações:
que nos conduz à equação de estados onde
Realização de estados
• Alem disso
Logo a equação de saída é dada por
y(kT) = Cx(kT) + Du(kT) onde
Realização de estados
• A representação de estados acima recebe o nome de forma canônica
de controlabilidade pois o par (A;B) nessa representação será sempre
controlável.
• Note que não existem zeros na função de transferência de U(z) para
R(z). Logo não pode haver cancelamento pólo/zero nessa parte do
sistema que define a ação de controle. Isso justifica que o sistema
seja controlável.
• Entretanto, se existem cancelamentos pólo/zero em G(z), isto é, de
U(z) para Y (z), esses cancelamentos ocorrem na função de
transferência de R(z) para a saída Y (z). Logo o sistema não será
observável.
• A matriz A com a estrutura acima recebe o nome de forma
companheira pois sua equação característica pode ser diretamente
escrita com a última linha de A, isto é,:
det(zI - A) = zq + a1zq-1 + ... + aq.
• Como a realização de estados de uma dada função de transferência
não é única existem outras formas de se obter a representação de
estados do sistema.
Realização de estados
• Para sistemas MIMO podemos obter a função de
transferência de cada entrada para cada saída,
como se fossem sistemas SISO desacoplados, e
em seguida acoplá-los, dois à dois, da seguinte
forma:
Realização de estados
• Realização Mínima: A realização de estado (A;B;C;D)
de um sistema é dita ser mínima se a matriz de
dinâmica A possui a menor dimensão possível.
• O procedimento para realização de estados descrito
acima é simples mas normalmente não conduz á
uma realização mínima. Para se obter uma
realização de estados mínima a partir de uma
realização não mínima basta se eliminar os estados
não controláveis e não observáveis, pois uma
realização (A;B;C;D) é mínima se e somente se (A;B)
é controlável e (A;C) é observável.
Pólos e zeros
• Como as matrizes do modelo são
constantes, i.e. o sistema é linear
invariante no tempo, podemos utilizar a
transformada Z para obter a matriz de
transferência do sistema. Para isso basta
supor condições iniciais nulas obtendo
Pólos e zeros
• Pólos: Um número complexo z é um pólo
de G(z) se ele é um pólo de pelo menos
uma das funções Gij(z).
• Todo pólo de G(z) é um autovalor de A,
porém o contrário não é verdade em
geral pois cancelamentos pólos/zeros
podem ocorrer nas funções Gij(z).
Podemos mostrar as seguintes relações:
Pólos e zeros
• Teorema 1 Seja G(z) = C(zI - A)-1B + D. Então
as seguintes afirmações são verdadeiras:
– Se (A;B) é controlável e (A;C) observável então
todos os autovalores de A são pólos de G(z).
– Se (A;B) é estabilizável e (A;C) detectável então
todos os autovalores de A localizados fora do
círculo unitário são pólos de G(z).
– Todos os autovalores de A que não são pólos de
G(z) ou são não controláveis ou não observáveis.
Pólos e zeros
• Para definir zeros de um sistema multivariável note que
dificilmente encontraríamos um número complexo z0 tal
que G(z0) = 0 já que isso implicaria que z0 é um zero
simultâneo de todos os elementos de G(z). Ao invés
disso definiremos zero de um sistema multivariável
como sendo um número complexo que anula
simultaneamente todas as saídas do sistema (ou uma
combinação delas) para algum sinal de entrada. Esta
definição de zeros para sistemas multivariáveis é mais
interessante pois nos permite levar em conta o
acoplamento entrada/saída do sistema. Para uma
definição formal de zeros, precisaremos da seguinte
definição auxiliar.
Pólos e zeros
• Posto normal: definimos posto normal de G(z) o maior posto de
G(z) qualquer que seja o complexo z.
• Por exemplo o posto normal de:
é 2, porém posto(G(0)) = 1. Assim o posto normal é o posto para a
maior parte dos valores de z, excluindo-se apenas alguns valores
para os quais existe redução do posto.
• Dizemos que G(z) possui posto normal completo se o posto normal
de G(z) coincide com o número de linhas ou colunas (o que for
menor), isto é se as linhas ou colunas de G(z) forem linearmente
independentes para a maior parte dos valores de z.
Pólos e zeros
• Zeros de transmissão: Seja G(z) uma matriz de posto
normal completo. Dizemos que z0 é um zero de transmissão
de G(z) se uma das condições abaixo está satisfeita:
– (i) Posto normal de G(z) é igual à q e existe um vetor v tal
que G(z0)v = 0.
– (ii) Posto normal de G(z) é igual à r e existe um vetor w
tal que wG(z0) = 0.
– (iii) G(z) é quadrada e det(G(z0)) = 0.
Veja na definição acima que se o posto de G(z) sofre
redução para algum z = z0 então podemos encontrar um
sinal de entrada v que pertence ao espaço nulo de G(z0) e
dessa forma a saída y(z0) = G(z0)v será nula para a entrada
v nos casos (i); (iii). No caso (ii) é uma combinação das
saídas que se anula pois wy(z0) = wG(z0)v será nula para
qualquer entrada v.
Pólos e zeros
• Uma forma alternativa de se definir zeros de um
sistema multivariável vem da utilização das
equações de estado ao invés da função de
transferência. Impondo saída nula e tomando a
transformada Z vemos que (zI - A)X(z) - BU(z) = 0
e CX(z) + DU(z) = 0 onde X(z); U(z) são as
transformadas de x(kT); u(kT) respectivamente.
De forma compacta temos:
Pólos e zeros
• Zero invariante: Um número complexo z0 é
chamado de zero invariante de uma
representação de estados se posto(R(z0)) é
inferior ao posto normal de R(z). Para verificar um
resultado interessante seja (v0; z0) um par
autovetor/autovalor de A, isto é AT v0 = z0 v0 e
suponha que v0* B = 0. Então o autovalor z0 não é
controlável pois v0* Mc = 0 e isto implica que o
posto da matriz de controlabilidade Mc é inferior
ao número de variáveis de estado. Além disso
note que [v0* 0] R(z0)=0. Logo todo autovalor não
controlável de A é um zero invariante do sistema.
Pólos e zeros
Por outro lado se A v0 = z0 v0 e C v0 = 0 então z0 é um
autovalor não observável de A já que Mc v0 = 0
indicando que o posto da matriz de observabilidade é
menor que o número de variáveis de estado. Além disso
note que R(z0) · [v0 ,0]T ¸= 0 Logo todo autovalor não
observável de A é um zero invariante do sistema. Para
X(z) = (zI - A)-1BU(z) a definição de zero invariante
recupera a definição de zero de transmissão. Assim,
todo zero de transmissão é também um zero invariante.
Num sistema controlável e observável o conjunto de
zeros invariantes e de transmissão coincidem. Para
G(z) quadrada com D inversível, então todo zero
invariante é um autovalor de A - BD-1C e todo zero de
transmissão é um pólo de G(z) -1.
Alocação de pólos para
sistemas de tempo discreto
• Para precisar o problema que gostaríamos de resolver, considere o
seguinte sistema linear discreto x(kT + T) = Ax(kT) + Bu(kT) onde
x(kT) representa o vetor de estados, u(kT) o sinal de controle, A;B são
matrizes constantes com dimensões apropriadas.
• Suponha que dispomos de medidores para todas as variáveis de
estado. Gostaríamos de determinar uma lei de controle do tipo
u(kT) = Fx(kT), onde F é a matriz de ganhos de realimentação a ser
determinada, de tal forma que o sistema em malha fechada satisfaça
os seguintes requisitos:
– (i) o regime permanente seja atingido, isto é o sistema seja
exponencialmente estável
– (ii) que a resposta transitória satisfaça certos critérios de
desempenho definidos pela localização desejada dos pólos do
sistema realimentado.
Alocação de pólos para
sistemas de tempo discreto
• O sistema em malha fechada com a lei
de controle u(kT) =Fx(kT) é dado por
x(kT + T) = (A + BF) x(kT) e para que
ele seja exponencialmente estável
todos os autovalores da matriz (A + BF)
devem estar no interior do círculo
unitário.
Realimentação de estados
com alocação de pólos
A motivação para resolver o problema acima, conhecido
como alocação de pólos, vem do fato de que a
localização dos pólos de malha fechada define a
estabilidade e está fortemente ligada ao comportamento
transitório do sistema. Assim, basta o projetista escolher
adequadamente a localização dos pólos de malha
fechada que o sistema de controle irá funcionar
adequadamente durante o transitório e atingindo o
regime permanente (estabilidade).
Observe entretanto que o transitório depende também
dos zeros do sistema e não apenas dos pólos. Para
acomodar a influência dos zeros, o projeto de alocação
de pólos é feito tipicamente de forma iterativa até que os
requisitos de resposta durante o transitório sejam
atingidos nas simulações.
Realimentação de estados
com alocação de pólos
• Para que possamos projetar os ganhos de
realimentação de forma a atingir o desempenho
desejado (a ser definido pelo projetista através da
escolha dos pólos de malha fechada) o sistema de
malha aberta precisa ser controlável .
• Quando o sistema de malha aberta é controlável
podemos escolher a localização dos pólos de malha
fechada de forma a encontrar uma realimentação de
estados que modifica os pólos da forma desejada. O
projeto dos ganhos de realimentação é bastante
simples no caso de sistemas com uma entrada e uma
saída (SISO) e referência nula
Referência nula: regulação
Para o sistema
x(kT + T) = Ax(kT) + Bu(kT)
seja uma mudança de coordenadas
Tw(kT) = x(kT) tal que o sistema
transformado se encontre na forma
canônica de controlabilidade, ou seja:
Referência nula: regulação
Onde
é o polinômio característico de malha aberta do sistema
SISO
Referência nula: regulação
Pode-se implementar a seguinte lei de
controle:
O problema que devemos resolver agora é
encontrar Fc de forma que o sistema em
malha fechada seja:
Referência nula: regulação
• Ora, a matriz Ac - BcFc está na forma companheira:
• Como desejamos que, em malha fechada, o sistema seja
estável e, ainda, atinja certas especificações de desempenho
associadas aos pólos desejados para a malha fechada,
queremos que os autovalores de malha fechada satisfaçam
uma dada equação característica escolhemos ai + fi = i;
• Ou seja, o vetor de ganhos para o sistema na forma canônica
controlável é Fc = [n - an ... 1 – a1 ]
Referência nula: regulação
• A lei de controle será implementada para o sistema
original, e não para o sistema transformado. Como
• Tem-se
• E importante notar que para que possamos calcular a
matriz de ganhos acima, que aloca os pólos nas posições
desejadas, é preciso que a matriz Mc seja inversível e isto
ocorre se e somente se o sistema for controlável. Apesar
da fórmula acima ser válida apenas para sistemas SISO,
a controlabilidade ainda é requisito necessário e suficiente
para alocação de pólos no caso MIMO
Método para sistemas MIMO
Dado o sistema em malha fechada:
ou seja, x(kT + T) = (A - BF)x(kT). Queremos
encontrar a matriz de ganhos F de tal forma que
os autovalores de (A - BF) sejam {1, ... , n}. Para
isso, devemos ter:
(A - BF)vi = ivi
sendo i autovalores e vi seus respectivos
autovetores.
Método para sistemas MIMO
Podemos reescrever na forma:
Lembrando que espaço nulo da matriz Mi é o
conjunto de todos os vetores gi ≠0 que satisfazem
Migi = 0, o problema a ser resolvido consiste em
encontrar (vi; F) tal que o vetor gi = [vi, Fvi] T
pertença ao espaço nulo da matriz Mi para todo
i = 1, ... , n.
Método para sistemas MIMO
Se particionarmos a matriz [g1 , ..., gn] de
acordo com os vetores vi e Fvi, obtemos:
Supondo V inversível podemos obter a
matriz de ganhos através da relação
F = GV -1
Observador de ordem
completa
Consideraremos agora o problema de estimar todas as variáveis
de estado de um sistema a partir dos sinais conhecidos disponíveis
nesse sistema. Para isso admitiremos que o sistema seja descrito
por
x(kT + T) = Ax(kT) + Bu(kT); x(0) = x0
y(kT) = Cx(kT)
onde x é o vetor de estados, u é a variável de controle que
suporemos conhecida e y é o sinal de saída do sistema
proveniente dos medidores e suporemos que não existe
redundância nas variáveis medidas, isto é posto(C) = ny.
Observe que, se o número de sensores for igual ao número de
variáveis de estado (ny =n), e as medidas efetuadas não são
redundantes (a matriz C é inversível) então podemos determinar o
estado através da relação algébrica x(kT) = C -1 y(kT).
Observador de ordem
completa
• No entanto, na grande maioria dos casos não
dispomos de sensores para todas as variáveis de
estado e nesses casos temos ny < n implicando
que a matriz C não é mais inversível e portanto
não mais podemos encontrar o estado através da
relação algébrica acima. A solução nesses casos
é obter uma estimativa xf (kT) do sinal x(kT)
através de um filtro dinâmico cujas entradas são
os sinais conhecidos do sistema y(kT); u(kT) e
cuja saída é a estimativa xf (kT),
Observador de ordem
completa
A representação de estados desse filtro é
indicada abaixo.
xf (kT + T) = Afxf (kT) + Bfu(kT) + Lfy(kT)
onde as matrizes Af ;Bf ;Lf devem ser
determinadas tais que as seguintes condições
sejam satisfeitas:
– (i) A estimativa xf (kT) deve convergir para x(kT) em
regime permanente, i.e.
– (ii) A dinâmica do erro de estimação
e(kT) = x(kT) -xf (kT) deve depender apenas da
condição inicial e(0) = x(0) - xf (0).
Observador de ordem
completa
• Um filtro que satisfaz as condições acima é
denominado de observador de Luenberger.
• O observador é denominado de ordem completa
quando o estado xf (kT) do observador possui
dimensão igual a do estado x(kT) que se deseja
estimar.
• O requisito (i) indica que não existe erro de
estimação em regime permanente, enquanto (ii)
indica que o erro de estimação não depende dos
sinais de entrada do filtro y(kT); u(kT) e portanto o
projeto do observador e da lei de controle ficam
independentes.
Observador de ordem
completa
• Para determinar as matrizes do filtro que
satisfazem as condições acima, basta
calcular a dinâmica do erro de estimação
e(kT) = x(kT) - xf (kT) que nos leva a:
Observador de ordem
completa
• Para que o requisito (i) seja atendido devemos
escolher
Af = A - LfC ; Bf = B
que resulta na seguinte dinâmica do erro de
estimação
e(kT + T) = (A - LfC)e(kT)
e num filtro, conhecido como observador de
Luenberger de ordem completa, dado pela
equação abaixo
xf (KT + T) = (A - LfC)xf (kT) + Bu(kT) + Lfy(kT)
Observador de ordem
completa
• Por outro lado para que o requisito (ii) seja
atendido devemos escolher a matriz Lf ,
conhecida como ganho do observador, de
tal forma que os autovalores da matriz ALfC, que define a dinâmica do erro, tenham
todos parte real negativa, pois dessa forma
teremos
e(kT) = (A - LfC)k e(0) ,
Técnicas para projeto do
ganho do observador
• O problema que queremos estudar consiste em projetar a
matriz Lf de ganho do observador de tal forma que os
autovalores da matriz A-LfC estejam no círculo unitário.
• Este problema é similar ao de projeto de realimentação de
estados, onde os autovalores da matriz A - BF devem ser
definidos. A única diferença é a posição das matrizes F e Lf
, a serem determinadas, em relação às matrizes
constantes B e C. No entanto, essa dificuldade pode ser
eliminada notando que os autovalores de A-LfC são os
mesmos da sua transposta AT - CT LfT onde agora LfT e F
aparecem na mesma posição.
Portanto podemos estabelecer
a seguinte correspondência:
Técnicas para projeto do
ganho do observador
• A tabela indica que se definirmos um sistema de controle
auxiliar fictício, chamado de sistema dual, na forma
ed(kT + T) = AT ed(kT) + CT ud(kT) ; ud(kT) = - LfT ed(kT)
onde ed(kT); ud(kT) são o estado dual e controle dual,
respectivamente, podemos utilizar as mesmas técnicas
da seção anterior para encontrar a matriz de ganho Lf tal
que o sistema dual acima em malha fechada AT - CT LfT
seja estável.
• Note que controlabilidade no sistema dual significa
observabilidade do par (A;C) que indica observabilidade
do sistema original. Isto decorre do fato de que a matriz
de controlabilidade do par (AT; CT ) é a transposta da
matriz de observabilidade do par (A;C).
Estabilidade segundo
Lyapunov
• Existem vários métodos para analisar estabilidade de
sistemas lineares, porem, o segundo método de
Lyapunov pode ser utilizado para analisar estabilidade
tanto de sistemas lineares quanto não lineares,
variantes ou invariantes no tempo.
• Sabe-se que um sistema é estável se a energia total
deste decresce continuamente ate atingir um estado de
equilíbrio. Esta idéia é utilizada no método de Lyapunov,
porem, para sistemas descritos por equações sem
relação direta com sistemas físicos não é uma tarefa
simples definir a “função energia”. Assim é introduzida
uma função de energia “fictícia” denominada função de
Lyapunov, que é uma função escalar que satisfaz as
hipóteses do teorema de estabilidade de Lyapunov.
Estabilidade segundo
Lyapunov
Estabilidade segundo
Lyapunov
Estabilidade segundo
Lyapunov
Estabilidade segundo
Lyapunov
• FIM