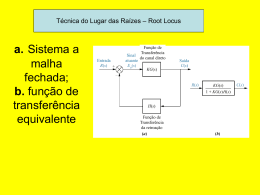
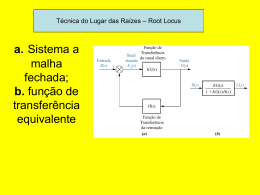
Projeto de Resposta Transitória através
do ajuste do Ganho de malha aberta
• Para utilizar os índices de desempenho de
segunda ordem temos que levar em
consideração:
– Pólos de ordem superior mais afastados do eixo
imaginário que os de segunda ordem;
– Zeros de malha fechada próximos aos pólos de
segunda ordem devem sofrer um efeito de
cancelamento de pólos de ordem superior;
– Zeros de malha fechada não cancelados pelos pólos
de ordem superior devem estar distantes dos pólos
de segunda ordem.
Fazendo aproximação de segunda ordem
Exemplo: Para o sistema abaixo. Projetar K
para %UP=1,52%. Calcule o Tempo de Pico, o
Tempo de Estabilização e erro de estado
estacionário
• Calcular a relação de amortecimento e o ângulo
da reta
• Cálculo dos pontos de chegada e saída
• Cálculo das assíntotas
• Esboçar o lugar das raízes
• Testar pontos do lugar das raízes que cruzam a
reta da relação de amortecimento e verificar o
ganho destes pontos
• Calcular os terceiros pólos
• Calcular o tempo de pico e de estabilização
utilizando os pólos dominantes
• Calcular os erros de velocidade
 1,52 
 ln

100


  1,52 
 0,8
 1,52 
 2  ln 2 

100


cos      cos1 0,8    36,870    1800  36,870  143,130
1
1
1
1
 

  1,5    1   10
 0,6213

2 3  15,5 2  33  15  0  raízes   2,7682
 4,3604

0  1  10   1,5  11 1,5
a 

 4,75
3 1
2
 1  900

2k  1


0
3 1


270
 2
1,5
k  7,36  Terceiro pólo  9,25
k  12,79  Terceiro pólo  8,6
k  39,64  Terceiro pólo  1,8
Respostas de
segunda e terceira
ordem para o
Exemplo anterior:
Lugar das Raízes Generalizado:
analisar a variação da posição
dos pólos de malha fechada para
variações nos valores outro
parâmetro
10

s  2 s  p1 
10
T s  
 2
10
s  2 s  10  p1 s  2 
1
s  2s  p1 
10
2

s  2
s

2
s

10
T s  
 1  KG s H s   1  p1 2
p1 s  2 
s  2 s  10
1 2
s  2 s  10

s  2
1  KG s H s   1  p1
s  1  3 j s  1  3 j 
Lugar das
raízes para o
sistema
anterior,
tendo p1
como
parâmetro
Plano s
Lugar das Raízes para sistemas com
retroação positiva
KG ( s )
T s  
1  KG s H s 
KG s H s   1
K G s H s   1
G s H s   k 360o , k  0,1,2.....
Regras para esboço do Lugar das
Raízes realimentação positiva
1. O número de ramos do lugar das raízes
é igual ao número de pólos do sistema;
2. O lugar das raízes é simétrico em
relação ao eixo real;
3. O eixo real que está a esquerda de um
número par de pólos e/ou zeros finitos
de malha aberta faz parte do lugar das
raízes;
Regras para esboço do Lugar das
Raízes realimentação positiva
4. O lugar das raízes se inicia nos pólos
finitos de malha aberta e termina nos
zeros finitos e infinitos de malha aberta;
5. Os ramos do lugar das raízes que vão
para infinito tendem a retas assintóticas
fornecidas pelas equações:
a 
a 
  pólos finitos   zeros finitos
Núm. pólos finitos 
Num. zeros finitos
2k
ondek  0,  1,  2 ,.....
Núm. pólos finitos  Num. zeros finitos
a. Sistema com retroação positiva;
b. lugar das raízes
C(S)
Exercícios Capítulo 8
• Exemplos: 1, 2, 4, 5, 6, 7, 8 e 9;
• Exercícios de Avaliação: 1, 2, 3, 4, 5, 6 e
7;
• Problemas: 1, 2, 3, 4, 5, 8, 9, 10, 11, 13,
14, 17, 21, 24 e 30.