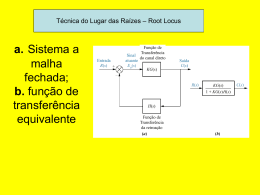
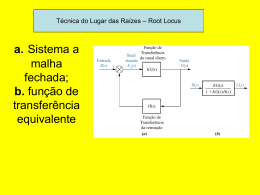
EST – 2002/2003
Método do Lugar Geométrico das Raízes (LGR) ou Root-Locus
A caracteristica básica da resposta transitória de um sistema em malha fechada é
determinada a partir dos pólos em malha fechada. Portanto, em problemas de análise, é
importante localizar os pólos em malha fechada no plano complexo.
No projecto de sistemas em malha fechada, pretende-se ajustar os pólos em malha
aberta de modo a colocar os pólos em malha fechada nas posições desejadas no plano
complexo.
Os pólos em malha fechada são raízes da equação caractertistica.
Um método simples para detreminar as raízes da equação carcteristica foi desenvolvida
por R. W. Evans e é extensivamente usado, denomina-se LGR ou Root-Locus.
É um método pelo qual as raízes da equação carcteristica são colocados em um gráfico
para todos os valores de um parâmetro do sistema. Este parâmetro é o ganhpo da função
de transferência em malha fechada e varia de 0 a +∞.
R(s)
G(s)
C(s)
H(s)
C ( s)
G ( s)
=
R( s) 1 + G ( s) H ( s)
A equação caracteristica é: 1 + G(s)H(s)=0
ou GH(s) = -1
É uma entidade complexa logo tem de ser desmembrada em termos
de módulo e ângulo
| GH(s) |=1 <= CONDIÇÃO DO MÓDULO
∠ GH(s)=±180º (2k+1) , k=0,1,2,3,... <= CONDIÇÃO DO ÂNGULO
Os valores de s que satisfazem as condições de ângulo e módulo são as raízes da
equação característica.
C ( s)
k
= 2
R( s) s + s + k
2
A equação característica é: s + s + k = 0
Deseja-se determinar o LGR desta equação confrome k varia de de 0 a +∞: k>0.
EXEMPLO: Gráfico do LGR para
Profª Sónia Marques
1
EST – 2002/2003
1 1
Raízes da equação carcterística: s = − ±
1 − 4k
2 2
Raízes reais duplas para k=1/4
Corresponde ao amortecimento critico
na resposta temporal
a um degrau unitário, onde ξ=1.
jω
K=+∞
Raízes reais distintas para 1 – 4 k > 0 ⇔ k < ¼
Corresponde ao sub-amortecimento na resposta temporal
a um degrau unitário, não apresentado oscilações.
Plano
complexo
K=0
K=1/4
K=0
σ
0
-1
Raízes complexas conjugadas
para 1 – 4 k < 0 ⇔ k >1/4
Corresponde ao sobre-amortecimento na resposta temporal
a um degrau unitário, apresentado oscilações.
Prova que qualquer ponto sobre o LGR satisfaz a condição de ângulo:
k
∠
= −∠s − ∠s + 1 = ±180(2k + 1),
k = 0,1,2,3,4,....
s ( s + 1)
K=+∞
jω
Plano
complexo
P1
+j
θ1
θ2
Ponto P1
-1
P2
0
1/ 2

θ
90
º
arctg
=
+
= 117 º
1
θ
s
∠
=


1
1
⇔ θ1 + θ 2 = 180º
⇔

1
∠s + 1 = θ 2
 θ 2 = arctg
= 63º
1/ 2

Ponto P2
 ∠s = θ1
θ = 180º
⇔ 1
⇔ θ1 + θ 2 = 180º

∠s + 1 = θ 2
 θ 2 = 0º
Os pontos que não estiveram localizados no LGR não satisfazem a condição de ângulo,
portanto não são pólos de cadeia-fechada para quaisquer valores de k.
Se os pólos de cadeia-fechada forem especificadas no LGR então o valor
correspondente de K é determinada pela condição do módulo.
Profª Sónia Marques
2
σ
EST – 2002/2003
EXEMPLO: s=-0.5±2j ⇒ GH ( s) =
k
= 1 ⇔ k = s( s + 1) s =−0.5+ 2 j = 17 / 4
s ( s + 1) s =−0.5+ 2 j
Basta fazer para um dos pólos complexos conjugados pois o outro é automaticamente
igual. No cálculo de k qualquer um dos pólos pode ser utilizado.
RESPOSTA TRANSITÓRIA: Efeitos da Variação de k
ξ=cte=0
ξ=cte
ωn 1 − ξ 2
k ↑⇒ ξ ↓ logo as oscilações aumentam na resposta temporal
a um degrau unitário.
α
ξ=cte
− ξωn
ω
α = arctg


n
 1−ξ 2
1 − ξ 2 
= arctg
 ξ
ξωn 

  ξ = 1 ⇒ α = 0º
⇒
 ξ = 0 ⇒ α = 90º

Corresponde ao eixo real negativo quando os pólos em malha fechada são
reais duplos. Na recta real negativa também existe ξ>1 que corresponde a
quando os pólos são reais distintos.
Corresponde ao eixo imaginário quando os pólos em
malha fechada são imaginários puros.
SUMÁRIO DAS REGRAS GERAIS PARA A CONSTRUÇÃO DO LGR(GANHO
POSITIVO k≥0)
•
Os ramos do LGR começam nos pólos da FT em cadeia aberta e terminam nos
zeros da FT em cadeia aberta ou no infinito (caso não existam zeros).
• Pertencem ao LGR os pontos da recta real que tenham à sua direita um número
ímpar de pólos e zeros.
• Comportamento assímptótico
Assímptotas: rectas para que tendem os ramos do LGR que vão para o infinito. É
igual ao número de pólos em malha aberta subtraído do número de zeros em
malha aberta (assímptotas = n-m).
Ângulo que as assímptotas fazem com o eixo real:
(1 + 2k )π
φ=
, k = 0,1,2,3,4,...., n − m − 1
n−m
Centro assimptótico: σ =
Profª Sónia Marques
n
m
j =1
i =1
∑ pólosKGH (s) − ∑ zerosKGH (s)
n−m
3
EST – 2002/2003
•
Ângulo de partida dos pólos complexos conjugados
m
n
i =1
j =1
θ j = ± (1 + 2k )π + ∑ γ i − ∑θ j
Contribuição
angular dos
restantes pólos
Contribuição
angular dos zeros
•
Ângulode
dechegada
partida do
pólo complexo
-pconjugados
j
Ângulo
a zeros
complexos
m
n
i =1
j =1
Contribuição
angular dos
pólos
γ j = ± (1 + 2k )π − ∑ γ i + ∑θ j
Contribuição angular
dos restantes zeros
Ângulo de chegada ao zero complexo -zj
•
Determinação do breakaway e breakin:
O ponto breakaway corresponde ao maior valor de k pra o qual as raízes da
equação caracteristica ainda são reais. O ponto breakin corresponde a um ponto
de entrada no eixo real em que se verifica um mínimo relativo no ganho k
1
Como calcular? Eq. Caracteristica: 1 + KGH ( s ) = 0 ⇔ K = −
GH ( s )
Pretende-se determinar o valor de s tal que k seja o máximo relativo:
δK
δK  1 

=0
=0⇔−
δs
δs  GH ( s ) 
• Ângulo de partida ou ângulo de chegada ao eixo real:
O ângulo entre dois ramos adjacentes que se aproximam (ou se afastam) do
2π
ou
mesmo ponto do eixo real é λ =
α
O ângulo entre dois ramos adjacentes um a chegar e o outro a partir do mesmo
ponto do eixo real é θ =
π
com α = nº ramos que se cruzam no ponto
α
considerado.
Profª Sónia Marques
4