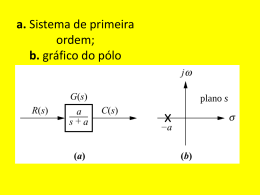
Disciplina: Sistemas de Controle 1 - ET76H
Prof. Dr. Ismael Chiamenti
2014/2
Aula 5
• CONTATOS PARA DÚVIDAS
- Email: [email protected]
-Local: DAELT/UTFPR
• PLANO DE ENSINO, PLANO DE AULAS E INFORMAÇÕES:
https://paginapessoal.utfpr.edu.br/chiamenti
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Conceitos básicos de sistemas de controle;
Sistemas em malha aberta e malha fechada;
(Revisão TL) e Simplificação de diagrama de blocos;
Funções de transferência ;
Modelo na forma de variáveis de estado;
Caracterização da resposta de sistemas de
primeira ordem, segunda ordem e ordem superior;
Erro de estado estacionário;
Estabilidade;
Introdução a controladores PID;
Sintonia de controladores PID;
Método do lugar das raízes;
Projeto PID via método do lugar das raízes;
Resposta em frequência;
Margens de ganho e fase e estabilidade relativa;
Projeto de controlador por avanço e atraso de fase;
Controlabilidade e Observabilidade.
Considerando uma entrada conhecida (ok!), e o modelo
matemático inserido em cada bloco, pergunta-se: quais os aspectos
significativos das respostas dos sistemas de primeira e segunda
ordem e de ordem superior ?
Estudamos duas formas de modelar matematicamente sistemas:
a) Funções de transferência (modelo no domínio da frequência s).
b) Espaço de estados, formado pela(s) equação(ões) de estado e pela(s)
equação(ões) de saída (modelo no domínio do tempo t).
O próximo passo, após os modelos serem obtidos, é analisar os sistemas
modelados para verificar o comportamento das suas respostas perante uma (ou
mais) entrada(s) conhecida(s) de teste.
Na aula de hoje analisaremos, prioritariamente, a resposta transitória dos
sistemas, em aulas posteriores a resposta estacionária.
A obtenção dos parâmetros das respostas dos sistemas pode ser realizada
aplicando-se diferentes entradas no sistema em análise, tipicamente um
pequeno rol de sinais bastam: degrau, impulso, rampa, parábola e cossenoidal.
A ordem dos sistemas: é determinada pela ordem da equação diferencial que
descreve o sistema ou, de forma equivalente, a ordem do denominador da
função de transferência após os termos comuns com o numerador serem
cancelados, ou ainda, ao número de equações de primeira ordem necessárias
para modelar o sistema através de espaço de estados.
A resposta dos sistemas: pode ser dividida em duas parcelas: a resposta
forçada e a resposta natural.
• A resposta forçada também é chamada de resposta de estado estacionário ou
solução particular.
• A resposta natural é também chamada de resposta homogenia.
Técnicas de análise das respostas: podem ser utilizadas: solução da equação
diferencial, transformada de Laplace ou pólos e zeros. A que fornecer
resultados satisfatórios, no menor tempo, será a melhor.
PÓLOS (1) valores da variável da transformada de Laplace, s, que fazem
com que a função de transferência assuma valor infinito ou (2) qualquer raiz
do denominador que seja comum as raízes do numerador.
Exemplo:
G(s) 
( s  1)(s  3)
( s  1,5)(s  3)(s  4)
p1  1,5; p2  3; p3  4
ZEROS (1) valores da variável da transformada de Laplace, s, que fazem com
que a função de transferência assuma valor zero ou (2) qualquer raiz do
numerador que seja comum as raízes do denominador.
Exemplo:
G(s) 
( s  1)(s  3)
( s  1,5)(s  3)(s  4)
z1  1; z2  3
Exemplo: Considere
um sistema modelado
por G(s):
Pólo na entrada → degrau na saída: resposta forçada;
Pólo na FT → resposta natural;
Zeros e pólos geram amplitudes das respostas nat. e for.
Forma geral da função de transferência de sistemas de primeira ordem:
C ( s)
1
1/
a
G( s) 



R( s) s  1 s  1 /  s  a
No domínio do tempo:

dc (t )
 c(t )  r (t )
dt
c(t )  ch (t )  c p (t )  Aet /  c p (t )
constante de tempo: τ
Exemplos de sistemas
de primeira ordem:
Ordem do polinômio do denominador: 1
Representação por diagrama de blocos da forma geral da função de
transferência de primeira ordem:
C ( s)
1
1/
a
G( s) 



R( s) s  1 s  1 /  s  a
Resposta ao degrau unitário:
G (s) 
 1  1 
C ( s )  G ( s ) R( s )  
 
 s  1  s 
C (s)
R( s)
Expandindo em frações parciais:
a1
a2
C (s)  
s s  1
C (s) 
a1  sG(s) s0  1
a2  s 1G(s) s1/  
1

1
1

 
s s  1 s s  1 / 
c(t )  1  e t / , para
t 0
Análise da resposta: c(t )  1  et /
G ( s) 
1
1/
a


s  1 s  1 /  s  a
Para t = 0, temos c(0) = 0
Para t → ∞, temos c(∞ ) = 1
Para t = τ, temos c(τ) = 0,632,
1
uma vez que e  1/ 2,7182818
Tr: tempo de subida (resposta), de 10% até
90% do valor final.
2,31 0,11 2,2


 2,2
a
a
a
Quanto menor τ, mais rápida a resposta Tr.
Tr 
dc(t )
1
 e t / 
dt t 0 

t 0
1

Ts: tempo de assentamento (estabilização),
2% do valor final (mas pode ser outra %)
Ts 
4
 4
a
Determinação experimental da função de transferência de primeira
ordem, método útil quando informações detalhadas do sistema não são
acessíveis:
Considerando a função de transferência na forma G ( s )  K , e aplicando
sa
uma entrada em degrau unitário:
1 K
K /a K /a
C (s) 


s sa
s
sa
Determinando K e a da resposta
experimental, determina-se a
função de transferência do sistema.
Exemplo: Em um sistema foi aplicada uma entrada do tipo degrau unitário.
O gráfico abaixo foi obtido como resposta a tal entrada. Determine o modelo
matemático do sistema usando função de transferência.

1
 0,25  a  4
a
K
 18  K  18 * 4  72
a
G (s) 
72
s4
Resposta do sistema para entrada do tipo rampa:
1
R( s)  2
s
 1  1 
C ( s )  G ( s ) R( s )  
 2 
 s  1  s 
1 
2
C ( s)  2  
s
s s  1
c(t )  t   et / , para
t 0
e(t )  r (t )  c(t )
e(t )   (1  et / )
e(t ) t   
Quanto menor o τ, menor será o erro de
estado estacionário.
(1o ordem e r(t): rampa)
Resposta do sistema para entrada do tipo impulso:
R( s )  1
1
1
C ( s)  G ( s) R( s) 
s  1
c(t ) 
1

e t / , para
t0
Para sistemas LIT (lineares e invariantes no tempo):
t
crampa (t )   cdeg rau (t )dt
cimpulso (t ) 
dt
d (1  e t / )
cimpulso (t ) 
dt
1 t /
cimpulso (t )  e , para
0
t
crampa (t )   (1  e t / )dt
0

crampa (t )  t    e
t
0

t /  t
0
crampa (t )  t    e t / , para
dcdeg rau (t )

t0
t0
Forma geral da função de transferência de sistemas de segunda ordem:

C ( s)
 2
R(s) s  2 n s  n2
2
n
d 2c(t )
dc(t )
2
2

2



c
(
t
)


n
n
n r (t )
2
dt
dt
n2
C ( s)
 K. 2
R( s )
s  2 n s  n2
n : Frequência natural de oscilação;
 : Coeficiente de amortecimento;
Pólos : p1, 2   n  jn 1   2
Exemplo: Determine a frequência de oscilação natural e o coeficiente de
amortecimento do sistema descrito pela seguinte função de transferência:
36
G(s)  2
s  4,2s  36
n2
C ( s)
 2
R(s) s  2 n s  n2
n2
C ( s)
 K. 2
R( s )
s  2 n s  n2
n2  36  n  6
4,2
2 n  4,2   
 0,35
12
K 1
Exemplo: Determine a frequência de oscilação natural e o coeficiente de
amortecimento do sistema descrito pela seguinte função de transferência:
9
G(s)  2
s  4,2s  36
n2
C ( s)
 2
R(s) s  2 n s  n2
n2
C ( s)
 K. 2
R( s )
s  2 n s  n2
n2  36  n  6
4,2
2 n  4,2   
 0,35
12
K  9
2
n
9
K
 0,25
36
A resposta dos sistemas de segunda ordem
2
podem ser classificadas em quatro categorias, Pólos : p1, 2   n  jn 1  
de acordo com os valores dos seus pólos:
A resposta dos sistemas de segunda ordem
2
podem ser classificadas em quatro categorias, Pólos : p1, 2   n  jn 1  
de acordo com os valores dos seus pólos:
Desempenho do sistema: considerando uma entrada em degrau e 0    1:

 1 
n2

C ( s)   2
2  
 s  2 n s  n  s 


1
 nt
2
c(t )  1 
e
cos(n 1   t   )u (t )
2
1 






  tan 
2 
1  

1
Resposta ao degrau unitário:
Resposta ao impulso:
 1


n2
 
  
n



C ( s)   2
1
c(t )  
e
2 
 s  2 n s  n 
 2  2  1
 2 1 n t


n
2  1
2
e
    2 1 n t



u (t )

0   1


 

 n t
2
n
c(t )  
e
sin n 1   t u (t )
2
 1  

 1


c(t )  n2te nt u (t )
Parâmetros de desempenho:
Mp: valor máximo da resposta;
Fv: valor final ou valor de regime permanente.
Parâmetros de desempenho (resposta ao degrau unitário):
1. Tempo de pico (Tp): tempo para a resposta atingir seu valor máximo.
Tp 

n 1   2
sendo a magnitude no instante t = Tp calculada por (para entrada em degrau):
cmáx . (t )  1  e


1 2
2. Tempo de subida (Tr): tempo para a resposta ir de 10% para 90% do seu
valor final.
3. Percentual de Overshoot (PO): valor máximo da resposta, expresso em
porcentagem do valor final da resposta.
 Mp  Fv 
PO%  100
%
 Fv 
PO%  100e


1 2
%

 ln(PO% / 100)
 2  ln 2 ( PO% / 100)
4. Tempo de assentamento (Ts): Tempo para que o valor da resposta não
oscile mais que 2% do seu valor final (usaremos sempre 2%).
Ts 
4
 n
, para
2%
Ts 
3
 n
, para
5%
Percentual de overshoot versus coeficiente de amortecimento:
cos( )  
Parâmetros no plano s :


Tp 

2
d
n 1  
Ts 
4
 n

4
d
, para
2%

 ln(PO% / 100)
 2  ln 2 ( PO% / 100)
Exemplo: Desenhar a região no plano
complexo para PO < 16 % e Ts < 2,5 s.
PO%
16
15
10
zeta
0,503
0,516
0,591
θ
59,7º
58,9º
53,7º
Ts
2,5
2,0
1,0
σd
1,6
2,0
4,0
ATIVIDADE (F)
Efeitos na resposta dos sistemas de segunda ordem devido a alteração do
local dos pólos:
Efeitos na resposta dos sistemas de segunda ordem devido a alteração do
local dos pólos:
Efeitos na resposta dos sistemas de segunda ordem devido a alteração do
local dos pólos:
p1,2  2  j 4,532
p1, 2  2  j 4,532,
p3  10
p1, 2  2  j 4,532,
p3  3
Caso o pólo adicional (acima
da segunda ordem) esteja
distante (no eixo real do
plano s) dos pólos de segunda
ordem 5 vezes ou mais, o
sistema pode ser aproximado
como um de 2º ordem.
OBSERVAÇÕES:
•O princípio de pólos dominantes deve ser utilizado quando não há zeros
próximos aos pólos dominantes;
• Com zeros próximos, a resposta é alterada significativamente;
• Com os pólos de alta ordem DISTANTES dos dominantes, as fórmulas
para tempo de pico, percentual de overshoot, tempo de assentamento e
tempo de subida continuam válidas.
ATIVIDADE (G)