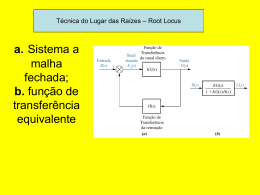
Regras para esboço do Lugar das
Raízes
1. O número de ramos do lugar das raízes
é igual ao número de pólos do sistema;
2. O lugar das raízes é simétrico em
relação ao eixo real;
3. O eixo real que está a esquerda de um
número ímpar de pólos e/ou zeros finitos
de malha aberta faz parte do lugar das
raízes;
Regras para esboço do Lugar das
Raízes
4. O lugar das raízes se inicia nos pólos
finitos de malha aberta e termina nos
zeros finitos e infinitos de malha aberta;
5. Os ramos do lugar das raízes que vão
para infinito tendem a retas assintóticas
fornecidas pelas equações:
a 
a 
  pólos finitos   zeros finitos
Núm. pólos finitos 
Num. zeros finitos
2k  1
Núm. pólos finitos 
Num. zeros finitos
onde k  0,  1,  2 ,.....
Exemplo: Esboce o
Lugar das raízes
Lugar das
raízes e
assíntotas
para o
sistema:
K s  3
F s  
ss  1s  2s  4
Plano s
Assíntota
Assíntota
 1,33
Assíntota
Refinando o Lugar das Raízes
1. Pontos de saída e pontos de chegada no
eixo real: m 1
n
1
  z    p
1
i
1
i
2. Cruzamento com o eixo imaginário é
feito através do critério de Routh
obtendo o valor do ganho que esta na
transição de estabilidade;
3. Ângulo de partida e chegada em pólos
ou zeros complexos conjugados
Pontos de Interseção com o Eixo
Imaginário
• Utilização do critério de Routh;
• Caso especial de linha que só possuem
zeros implicam na existência de
polinômios estritamente pares ou ímpares
como fator do polinômio original;
• Os polinômios pares possuem somente
raízes simétricas nas seguintes situações:
Localização
das raízes para
a geração de
polinômios
pares: A, B, C
ou qualquer
das
combinações
Plano s
A: Reais e simétricas em relação à origem
B: Imaginárias e simétricas em relação à origem
C:Quadrantais e simétricas em relação à origem
Pontos de Interseção com o Eixo
Imaginário
• Portanto só teremos raízes no eixo
imaginário se tivermos uma linha
contendo todos os termos iguais a zero na
tabela de Routh;
• Estas raízes são as raízes do “polinômio
par” que é o polinômio da linha acima da
linha de zeros;
• Tudo o que acontece na tabela de Routh
abaixo da linha do “polinômio par” se
refere a ele.
Tabela de Routh para:
T s  
10
s 5  7 s 4  6s 3  42 s 2  8s  56
Linha
Toda de
Zeros
Raízes de
Ps   s 4  6s  8
0 + 2.0000i
0 - 2.0000i
0 + 1.4142i
0 - 1.4142i
20
T s   8
s  s 7  12 s 6  22 s 5  39 s 4  59 s 3  48 s 2  38 s  20
Linha
Toda de
Zeros
0 + 1.4142i
0 - 1.4142i
0 + 1.0000i
0 - 1.0000i
0.5000 + 3.1225i
0.5000 - 3.1225i
0.0000 + 1.4142i
0.0000 - 1.4142i
-1.0000 + 0.0000i
-1.0000 - 0.0000i
-0.0000 + 1.0000i
-0.0000 - 1.0000i
Para o Exemplo Anterior temos:
• Ponto de Partida:
1
1
1
1
1




  3   0  1   2   4
3 4  26 3  77 2  84  24  0
Cujas Raízes valem:
 3,311 0,6812j
 1,6097
Ponto de Partida, pois é a única raíz que esta
 0,4349
entre “0” e “-1”
Para o Exemplo Anterior temos:
• Cruzamento com Eixo Imaginário
K s  3
F.T .M.F. 4
s  7 s 3  14s 2  8  K s  3K
Critériode Routh
s4
s3
s2
1
14
7
8 K
90  K
21K
2
1  K  65K  720
0
s
90  K
0
s
21K
0
3K
0
0
0
0
Linha de Zeros
Para o Exemplo Anterior temos:
 K 2  65K  720  0
ou
K 2  65K  720  0 cujas Raízes valem:
K1  74,65
K 2  9,65
Valor a ser Escolhido
Para K  9,65 o Polinômiopar 90  K s 2  21K fica dado por :
80,35s 2  202,7  0
s1, 2  1,587 j
Cruzamento com o Eixo Imaginário