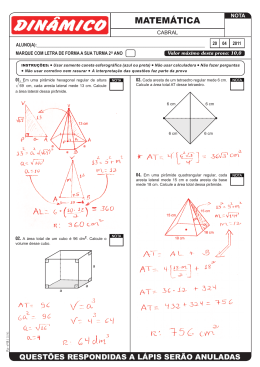
TRABALHO DE DEPENDÊNCIA
TURMA: 2ª SÉRIE
CONTEÚDOS RELATIVOS AO 1º E 2º BIMESTRE
MATEMÁTICA 2
PROFESSOR ROGERIO
1) AS
OBSERVAÇÕES:
QUESTÕES OBRIGATORIAMENTE DEVEM SER
ENTREGUES EM UMA FOLHA A PARTE COM ESTA EM
ANEXO;
2) NÃO SERÃO ACEITAS RASURAS;
3) TODAS AS QUESTÓES DEVEM VIR COM CÁLCULO OU
JUSTIFICADA. INCLUSIVE AS OBJETIVAS;
4) OS ALUNOS DEVEM PROCURAR SEUS PROFESSORES
PARA TIRAREM QUALQUER DÚVIDA, OU CASO
QUEIRAM, PODEM MONTAR GRUPO DE ESTUDO,
PORÉM É IMPORTANTE QUE TIREM SUAS DÚVIDAS E
ESTUDEM ATRAVÉS DOS CONTEÚDOS ABORDADOS EM
SEU TRABALHO PARA A PROVA DO PRÓXIMO
BIMESTRE.
1) Dada a figura a seguir e sabendo-se que os dois quadrados possuem lados
iguais a 4cm, sendo O o centro de um deles, quanto vale a área da parte
preenchida?
2) A área A de um triângulo pode ser calculada pela fórmula:
onde a, b, c são os comprimentos dos lados e p é o
semi-perímetro. Calcule a área do triângulo cujos lados medem 21, 17 e 10
centímetros.
3) De uma chapa quadrada de papelão recortam-se 4 discos, conforme
indicado na figura. Se a medida do diâmetro dos círculos é 10 cm, qual a
área (em cm2) não aproveitada da chapa?
4) Na figura seguinte, estão representados um quadrado de lado 4, uma de
suas diagonais e uma semicircunferência de raio 2. Então a área da região
hachurada é:
5) Um terreno tem a forma de um trapézio retângulo ABCD, conforme mostra
a figura, e as seguintes dimensões:
= 25 m,
= 24 m,
= 15 m.
Se cada metro quadrado desse terreno vale R$ 50,00, qual é o valor total do terreno?
6) Na figura a seguir tem-se uma circunferência C de centro O e raio de
medida 3 cm. Os pontos A e B pertencem a C, e a medida do ângulo AÔB
é 45°.
Qual a área da região sombreada, em centímetros quadrados?
7) Considere a região R, pintada de preto, exibida a seguir, construída no
interior de um quadrado de lado medindo 4 cm.
Sabendo-se que os arcos de circunferência que aparecem nos cantos do quadrado
têm seus centros nos vértices do quadrado e que cada raio mede 1 cm, determine a
área da região R.
8) A área do triângulo equilátero OAB, representado na figura a seguir é 9√3
cm2. Qual a área do círculo de centro O e tangente ao lado AB do triângulo,
em centímetros quadrados?
9) Numa esquina cujas ruas se cruzam, formando um ângulo de 120°, está
situado um terreno triangular com frentes de 20 m e 45 m para essas ruas,
conforme representado na figura a seguir:
Qual a área desse terreno, em m2?
10) O ponto O é o centro de uma circunferência de raio r, conforme a figura. Se
r = 4 cm, calcule área da região sombreada.
11) Calcule o número de vértices de um poliedro convexo considerando que ele
tem 2 faces quadrangulares e 8 faces triangulares.
12) Um poliedro convexo de 15 arestas tem apenas faces quadrangulares e
pentagonais. Considerando que a soma das medidas dos ângulos das
faces é igual a 2880°, determine o número de faces de cada tipo.
13) Qual a distância entre os centros de duas faces adjacentes de um cubo de
aresta 4?
14) Calcule a área lateral e a área total de um prisma quadrangular regular de
aresta lateral medindo 8 cm e aresta da base medindo 2,5 cm.
15) Num prisma regular de base hexagonal, a área lateral mede 36 m2 e a
altura é 3 m. Determine a medida da aresta da base.
16) Considere um prisma reto em que a base é um triângulo retângulo cujos
catetos medem 5 cm e 12 cm. Calcule a área total desse prisma
considerando que as arestas laterais medem 8 cm.
17) Calcule o volume ocupado por uma caixa de papelão em forma de
paralelepípedo reto - retângulo cujas medidas são 18 cm, 12 cm e 9 cm.
18) Uma caixa de água tem forma cúbica com 1 m de aresta. Quanto baixa o
nível da água ao retirarmos 1 litro de água da caixa?
19) Qual a capacidade, em litros, de um reservatório em forma de
paralelepípedo retângulo, cujas dimensões são 50 cm, 2 m e 3 m.
20) Considere um paralelepípedo com 12 m de comprimento, 4 m de largura e
3 m de altura. Se o seu volume for aumentado de 624 m3, de quanto
aumentará sua altura?
21) Calcular a área lateral de uma pirâmide regular quadrangular de altura 4 cm
e área da base 64 cm2.
22) A área total de uma pirâmide regular, cuja base é um triângulo equilátero de
lado x, é 5 vezes a área da base.
a) Expresse a área total dessa pirâmide em função do lado da base x.
b) Obtenha em função de x a área lateral dessa pirâmide.
23) Determine a área lateral da pirâmide hexagonal regular, cuja altura é h =
33 cm e o lado da base é 2 cm.
24) Uma pirâmide quadrangular regular tem 8 m de altura e 10 m de apótema.
Calcule sua área total.
25) Considere um cubo de aresta igual a 1 cm. Podemos obter uma pirâmide
tendo uma das faces desse cubo como base da pirâmide e o ponto situado
no centro da face oposta como vértice. Observe a figura e depois responda
às questões.
a)
Qual é a área lateral dessa pirâmide?
b)
Qual é a área total dessa pirâmide?
c)
Qual é a razão entre a área total do cubo e a da pirâmide, nessa
ordem?