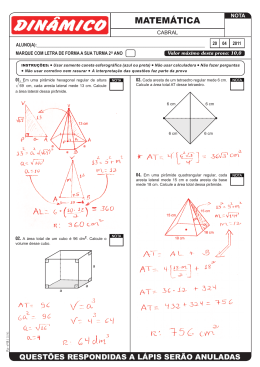
ACOMPANHAMENTO PEDAGÓGICO PARCIAL
APP - 1
2
3º BIMESTRE
ALUNO:
DATA :
SÉRIE/TURMA: 2ºMC
Nº
/ 08 /2013
PERIODO: MANHÃ
TARDE
C.CURRICULAR: MATEMÁTICA
PROF: MÁRCIO CÉSAR
REFERÊNCIA: PAG. _____ À PAG._______
NOTA:
DATA PARA DEVOLUÇÃO
CIENTE
____/ ____/ ____
____/ ____/ ____
Pai ou responsável
______________________
Assinatura
1 )A aresta lateral de uma pirâmide regular quadrangular mede 13 cm e a aresta da base, 5 2 cm.
Calcule seu volume. (2,0)
Repare que d/2 é metade da diagonal do quadrado dada por (l 2 ). Logo d = (5 2 .
plano da base. Logo forma um triângulo retângulo com (a) e (d/2). Calculando h, vem:
2 ) = 10. Logo d/2 = 5. A altura h é perpendicular ao
h  132  5 2  144  12.
A área da base é (5
2 )2 = 50cm2. O volume é calculado como (Sb. h)/3 = (50cm2. 12cm)/3 = 200cm3.
2) Seja o paralelepípedo da figura, de dimensões 5, 3 e 2. Calcule a diagonal do paralelepípedo. (2,0)
d2 = 52 + 32 = 25 + 9 = 34
A segunda figura mostra outro triângulo retângulo onde um dos catetos é a diagonal da base. Logo,
D2 = 22 + d2 = 4 + 34 = 38. Calculando, temos:
D  38.
3)Uma pirâmide quadrangular regular tem 3 m de altura e 8 m de aresta da base. Calcule a área total
e o volume desta pirâmide. (1,0)
O apótema da base da pirâmide é metade do lado do quadrado. Logo m = 4. Calculando g, temos:
g  4 2  32  25  5. As áreas da base e lateral são:
Sb = 82 = 64cm2
Sl = 4.(8.5)/2 = 80cm2
Logo a área total será 64cm2 + 80cm2 = 144cm2. O volume é calculado como (S b. h)/3 = (64cm2. 3cm)/3 = 64cm3.
4) Calcule a área lateral e o volume de um prisma reto de base triangular, cujas arestas da base medem
6 cm, 8 cm e 10 cm e cuja aresta lateral mede 20 cm. (1,0)
10
6
8
20
a) A área lateral será a soma das áreas de cada face. Ou o produto do perímetro da base pela altura. O perímetro da base é: 1 0 + 6 +8 = 24cm.
Logo,
Al  (24).h  24.20  480cm 2 .
b) O volume será o produto da área da base pela altura. Observando com atenção os lados da base, vemos que são múltiplos de 3 , 4 e 5. Logo ele é
retângulo. A área será a metade do produto dos catetos. Então,
V (
6 x8
).20  24.20  480cm 3 .
2
5) Num prisma reto, cada uma das bases é um retângulo em que um lado é o dobro do outro. A altura
do prisma mede 12 cm e a área total, 352 cm2. Calcular as dimensões do prisma. (2,0)
Solução.
A área total é dada por:
At  2(2 x)(12)  2( x)(12)  2( x)(2 x)  352cm 2 .
48x  24 x  4 x 2  352  4 x 2  72 x  352  0.
Resolvendo, temos:
Dividindo a equação por 4, temos: x2 + 18x – 88 = 0. Ou (x +
22)(x – 4) = 0. As raízes são: x = -22 ou x = 4. Como x representa uma medida, deve ser positivo. Logo as dimensões são: 4cm e 8cm.
6) Qual é a distância entre os centros de duas faces adjacentes de um cubo de aresta 4? (1,0)
A distância é dada por: é
d 2  22  22  8. Calculando a raiz quadrada temos: d  8  2 2.
7) A área total de um cubo é 24 m2. Calcule o volume desse cubo. (1,0)
A área total do cubo é
Logo
At  6a 2  24m 2 .
V  a 3  23  8m3 .
Calculando a aresta da base temos:
6a 2  24  a 2 
24
 4  a  4  2m.
6