FUNDAMENTOS DE
CONTROLE E AUTOMAÇÃO
Aula 9 – Lugar das raízes (root-locus)
Prof. Marcio Kimpara
Universidade Federal de
Mato Grosso do Sul
Sistema de controle
 A característica básica da resposta transitória de um sistema de malha
fechada, depende essencialmente da localização dos pólos de malha fechada;
 Permite estudar a evolução das raízes de uma equação, quando um parâmetro
é variado continuamente;
 É importante, então, que o projetista saiba COMO os pólos de malha fechada
se movem no plano s, a medida que o ganho de malha varia (compensador);
 O método do Lugar das raízes (root-locus) permite que as raízes da equação
característica sejam representadas graficamente para todos os valores do
ganho k.
Prof. Marcio Kimpara
2
Lugar das raízes
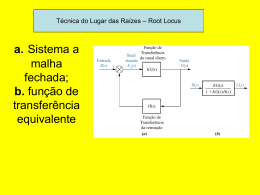
Iniciemos nosso estudo sobre o método do lugar das raízes considerando o
sistema com realimentação mostrado a seguir:
R(s)
+
C(s)
K
G(s)
H(s)
Vamos avaliar a influência do ganho K sobre os
pólos do sistema em malha fechada. A função de
transferência do sistema em malha fechada é:
Logo, desejamos estudar a equação:
Y ( s)
K .G(s)

R( s) 1  K .G(s).H (s)
1  K .G( s).H (s)  0
0  K  
Prof. Marcio Kimpara
3
Lugar das raízes
EXEMPLO:
Considere o seguinte sistema de controle:
R(s)
+
5
s ( s  20 )
Ka
C(s)
1
• Resolvendo
a
equação
do
denominador da função de transferência
de malha fechada, encontramos as
raízes em função de Ka
5.K a
5K a
Y (s)
ss  10 

 2
R( s ) 1  5.K a
s  20 s  5K a
ss  20 
Prof. Marcio Kimpara
4
Lugar das raízes
• Podemos verificar a posição dos pólos de malha fechada (lugar das
raízes) para o sistema dado, fazendo Ka variar de 0 a  
Da equação anterior, os polos a malha fechada são:
 20  20 2  4.5.K a
 10  100  5K a
2
Os
Variando o valor de Ka, podemos montar
a tabela ao lado:
Prof. Marcio Kimpara
5
Lugar das raízes
Para K a  0 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
Os
Re(s)
x
-20
Prof. Marcio Kimpara
x
0
6
Lugar das raízes
Para K a  1 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
Os
Re(s)
xx
-19.75
Prof. Marcio Kimpara
xx
-0.25
7
Lugar das raízes
Para K a  5 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
Os
Re(s)
xx x
-18.66
Prof. Marcio Kimpara
x xx
-1.34
8
Lugar das raízes
Para K a  10 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
Os
Re(s)
xx x x
-17.07
Prof. Marcio Kimpara
x x xx
-2.93
9
Lugar das raízes
Para K a  20 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
Os
Re(s)
xx x x
x
x x xx
-10
Prof. Marcio Kimpara
10
Lugar das raízes
Para K a  30 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
x -10+j7,07
Os
Re(s)
xx x x
x
x x xx
x -10-j7,07
Prof. Marcio Kimpara
11
Lugar das raízes
Para K a  40 temos o seguinte plote dos polos a malha fechada no
plano complexo
Imag(s)
x -10+j14.14
x
Os
Re(s)
xx x x
x
x x xx
x
x -10-j14.14
Prof. Marcio Kimpara
12
Lugar das raízes
Para K a   temos o seguinte plote dos polos a malha fechada no
plano complexo

Imag(s)
x
x
Os
Re(s)
xx x x
x-10 x x x x
x
x

Prof. Marcio Kimpara
13
Lugar das raízes
O gráfico do Lugar geométrico das raízes, consiste no esboço da posição de
todos os valores que os pólos de malha fechada de uma função de transferência
assumirão num plano de coordenadas complexas.
EXEMPLO: Considere o sistema de controle abaixo:
Os
Função de transferência à malha fechada:
Prof. Marcio Kimpara
Lugar das
raízes
14
Lugar das raízes
A característica básica de resposta transitória de um sistema de malha fechada,
depende essencialmente da localização dos pólos de malha fechada. Para cada
posição dos pólos a resposta transitória será diferente.
Demonstração: acesse o simulador disponível em:
http://www.wiley.com/college/nise/0471794759/swf/SOcalculator.swf
e altere a localização dos polos (clicando e arrastando) e observe a resposta
Daí a importância que o projetista saiba como os pólos de malha fechada se
movem no plano s, a medida que o ganho varia.
De acordo com a resposta desejada, deve-se buscar a localização dos pólos que
dão origem a tal resposta.
Mas como podemos esboçar o lugar das raízes?
Prof. Marcio Kimpara
15
Lugar das raízes
Solucionando a equação característica...
Contudo, a análise dos pólos através da solução da equação característica
apresenta limitações para sistemas de grau superior a 3, pois se torna
muito trabalhoso e requer métodos computacionais para encontrar a
solução
Além disto, trata-se de uma análise estática, pois, se o ganho variar, os
cálculos deverão ser refeitos.
Portanto, o objetivo do método do lugar das raízes é estabelecer regras
simples para representar graficamente as raízes do denominador da
função de transferência em malha fechada para todos os valores de K,
porém sem o conhecimento explícito das raízes.
Prof. Marcio Kimpara
16
Esboçando o lugar das raízes
O processo de construção do “lugar das raízes” de um sistema a malha
fechada se torna bem simples se aplicarmos os passos apresentados abaixo:
E
S
B
O
Ç
O
R
E
F
I
N
A
M
E
N
T
O
1o Passo: Determinar o número de ramos
2o Passo: Simetria
3o Passo: Pontos de inicio e término do lugar das raízes
4o Passo: Determinar o lugar das raízes sobre o eixo real
5o Passo: Comportamento no infinito Os
6o Passo: Determinar o ponto de partida ou chegada do eixo real
7o Passo: Determinar o ângulo de partida ou chegada no eixo real
8o Passo: Determinar o ângulo de partida e chegada dos polos ou zeros complexos
9o Passo: Determinar o ponto de cruzamento com o eixo imaginário
Prof. Marcio Kimpara
17
Procedimentos para esboço
1ª REGRA: Determinar o número de ramos
Ramo é o caminho percorrido pelo pólo quando variamos o ganho k.
O número de Ramos será SEMPRE igual ao número
de pólos do sistema a malha fechada
Ramo 1
Voltemos ao caso do exemplo com o sistema de
controle da posição da câmera, cuja FT Os
em malha
fechada é dada por:
Ramo 2
O sistema possui dois polos e, portanto, o lugar das
raízes terá 2 ramos (caminhos)
Prof. Marcio Kimpara
18
Procedimentos para esboço
2ª REGRA: Simetria
O lugar geométrico das raízes é simétrico em relação ao eixo real.
3ª REGRA: Pontos de início e término
O lugar das raízes se inicia nos polos, finitos ou infinitos de G(s).H(s) e termina nos
zeros de G(s).H(s).
O número de pólos é sempre igual ao número de zeros, lembrando que estes
podem ser finitos ou infinitos.
Os
Por exemplo, a FT abaixo tem 3 pólos finitos e nenhum zero finito, porém se analisarmos o
comportamento desta função no infinito, veremos que:
K
s.s  1
. s  4
• Se a função tender ao infinito, quando ‘s’ tender ao infinito, então a
função terá um ou mais pólos no infinito.
• Se a função tender a zero quando ‘s’ tender ao infinito, então, a função
terá um ou mais zeros no infinito.
Neste caso, fazendo ‘s’ tender ao infinito, tem-se 3 zeros no infinito.
Prof. Marcio Kimpara
19
Procedimentos para esboço
4ª REGRA: Determinar o lugar das raízes no eixo real
Um ponto no eixo real faz parte do lugar das raízes se o número total de pólos e
zeros no eixo real à direita do ponto for ÍMPAR.
Considere a função de transferência:
K .s  2
s.s  1
. s  3
. s  4
No eixo real, o lugar das
raízes existe à esquerda
de um número ímpar de
pólos e/ou zeros finitos
que estejam sobre o eixo
real.
Desenhando os pólos e zeros no plano complexo:
Os
Imag(s)
Re(s)
x x
-4
-3
-2
x x
-1
Aplicando
a
regra
acima, determinamos
os locais sobre o eixo
real pertencentes ao
lugar das raízes
Imag(s)
Re(s)
x x
0
-4
Prof. Marcio Kimpara
-3
-2
x x
-1
0
20
Procedimentos para esboço
5ª REGRA: Comportamento no infinito (caso exista)
O lugar das raízes tende a retas assintóticas quando o lugar tende ao infinito. A
equação das assíntotas é dada pelo ponto de interseção  a sobre o eixo real e o
ângulo  a de partida do eixo real:
a 
 polos finitos   zeros finitos
a 
Qtde polos finitos  Qtde zeros finitos
Os
2K  1.
Qtde polos finitos  Qtde zeros finitos
• O ângulo é dado em radianos no sentido trigonométrico a partir do eixo real positivo.
• O índice K fornece uma multiplicidade de retas. O número de retas obtidas é igual à
diferença entre o número de pólos finitos e o número de zeros finitos.
Prof. Marcio Kimpara
21
Procedimentos para esboço
5ª REGRA: Comportamento no infinito (caso exista)
EXEMPLO: Considere o sistema:
K s  3
s.s  1
. s  2
. s  4
Como existem zeros no infinito, precisamos das
assíntotas para direcionar o esboço do lugar das raízes
• O ponto de interseção com o eixo real é dado por:
1  2  4   3   4  1,33
a 
4 1
Os
3
• Os ângulos das retas valem:
a 
2K  1
3
 
3

 
 5
 3
para k  0
para k  1
para k  2
Prof. Marcio Kimpara
22
Procedimentos para esboço
6ª REGRA: Determinar os pontos de partida e chegada no eixo real
Se o lugar das raízes localiza-se entre dois pólos adjacentes no eixo real, existe no
mínimo um ponto de saída. Se o lugar das raízes localiza-se entre dois zeros
adjacentes no eixo real, existe no mínimo um ponto de entrada. Se o lugar das
raízes está entre um zero e um polo no eixo real, pode não existir nenhum ponto de
entrada ou saída.
EXEMPLO: Considere um sistema Os
de
controle, cujos pólos sejam 1+j1 e 1-j1, e os
zeros sejam -2 e -3.
Imag(s)
j1
-3
1
-2
-j1
Prof. Marcio Kimpara
x
Re(s)
x
23
Procedimentos para esboço
6ª REGRA: Determinar os pontos de partida e chegada no eixo real
Pela regra 4, podemos descobrir os segmentos sobre o eixo real que fazem parte
do lugar das raízes
Imag(s)
Pela regra 3, como existem dois zeros adjacentes
no eixo real, existe um ponto de chegada entre
estes dois zeros. Para encontrar o valor exato
deste ponto, usaremos a seguinte expressão:
m
n
1
1

1   z 1   p
i
i
onde:
Os
j1
-3
m  n  de zeros
n  n  de polos
zi  zeros finitos
Para o exemplo dado:
pi  polos finitos
Prof. Marcio Kimpara
1
-2
  ponto de partida ou chegada
x
-j1
Re(s)
x
 z1  2
 z  3
 2

 p1  1  j1
 p2  1  j1
24
Procedimentos para esboço
6ª REGRA: Determinar os pontos de partida e chegada no eixo real
Substituindo na expressão anterior:
2  5
2  2
 2
  5  6   2  2
1
1
1
1



  (2)   (3)   (1  j1)   (1  j1)
  3    2  1  j   1  j

  2.   3
 2  2  2
-3
j1
-2,43
-j1
x
1,29
 
 2,43
x
1
-2
7 2  8  22  0
Os
Imag(s)
Ponto de
chegada no
eixo real
2
Este ponto não pertence ao
lugar das raízes
Re(s)
x
Prof. Marcio Kimpara
25
Procedimentos para esboço
7ª REGRA: Determinar os ângulos de partida e chegada no eixo real
Ainda considerando o exemplo anterior, sabemos que o lugar das raízes sairá dos
polos complexos e terminarão nos zeros, entrando no eixo real pelo ponto -2,43. Mas,
como será a trajetória do lugar das raízes?
Uma forma de refinar o esboço do lugar das raízes é determinar o ângulo de chegada
no eixo real.
Os
180 
 chegada 
n
j1
n  n de polos
 chegada  90 
Imag(s)
x
90°
-3
1
-2
-2,43
-j1
Prof. Marcio Kimpara
Re(s)
x
26
Procedimentos para esboço
8ª REGRA: Determinar os ângulos de partida/chegada dos polos/zeros complexos
A partir de um dos pólos, traçamos retas que ligam cada pólo e
cada zero ao polo de referência (a um ponto bem próximo a ele)
1
1  a tan    18.43
 3
Imag(s)
j1
-3
2
x
Imag(s)
j1
-3
2
1
1
-2
3
Os
1
-j1
x
1
Re(s)
3  90

-j1
Imag(s)
-2 1
x
x
Re(s)
3  90
j1
2
-3
1
 2  a tan    14.03
4
x
1
-2
Prof. Marcio Kimpara
1
4
1
Re(s)
3  90

-j1
x
27
Procedimentos para esboço
8ª REGRA: Determinar os ângulos de partida dos polos complexos
 angulos dos zeros   angulos dos polos  180
1   2   3   X  180 
 X  122 .4



2  14.03

Imag(s)
j1
-j1
j1

-2 1  18.43
1
-j1

x
x
Re(s)
3  90
x
1
-2
-3
Os
122.4
-3
X

18.43  14.03  90   X  180

Imag(s)

x
Re(s)
Simetria em relação ao eixo real
122.4
Prof. Marcio Kimpara
28
Procedimentos para esboço
9ª REGRA: Cruzamento com o eixo imaginário (quando existir)
A importância desta regra pode ser notada claramente. Se olharmos
para a figura abaixo, podemos observar que os polos a malha
fechada estão no semi-plano esquerdo apenas até um certo valor de
ganho. Acima deste valor, dois dos polos se moverão para o semiplano direito, significando que o sistema se tornará instável.
O ponto de cruzamento com o eixo imaginário
será portanto o ponto no lugar das raízesOs
que
separa a operação estável da operação
instável do sistema. O valor do ω no ponto de
cruzamento será a frequência de oscilação.
Para encontrar o ponto jω de cruzamento,
utilizamos o critério de Routh-Hurwitz.
Prof. Marcio Kimpara
29
Procedimentos para esboço
9ª REGRA: Cruzamento com o eixo imaginário (quando existir)
Exemplo:
K s  3
s 4  7 s 3  14 s 2  8  K s  3K
s4
1
14
3K
0
s3
7
8 K
0
0
90  K
21K
0
0
 K 2  65 K  720
90  K
0
0
0
0
0
0
Os
s2
s
* OBS: A tabela foi simplificada
pelo fator 7 na segunda coluna
1
s0
21K
Prof. Marcio Kimpara
30
Procedimentos para esboço
9ª REGRA: Cruzamento com o eixo imaginário (quando existir)
Pelo critério de Routh, o sistema é estável quando não houver alteração de sinal
na 2° coluna. Como nas duas primeiras linhas temos valores positivos, devemos
ter:
1) 90  K  0
K  90
2)  K 2  65 K  720
0
90  K
Valor positivo
Os
Valor positivo
Como K< 90 (primeira exigência), o denominador será positivo. Logo:
 K 2  65 K  720  0
Prof. Marcio Kimpara
31
Procedimentos para esboço
9ª REGRA: Cruzamento com o eixo imaginário (quando existir)
Resolvendo a inequação:
 K 2  65K  720  0

 K 2  65 K  720  0
Raízes:
-74,65
<0
0
>0
Região que satisfaz
a inequação
9,65
<0
K1  74,65
K 2  9,65
Os
Eixo Reais
Assumindo valores positivos para
o ganho, concluímos que:
0  K  9,65
Prof. Marcio Kimpara
32
Procedimentos para esboço
9ª REGRA: Cruzamento com o eixo imaginário (quando existir)
Sabendo que 9,65 é o valor máximo de K para que o sistema continue estável e
sabendo-se que o sistema se torna instável quando os pólos passam para a
região do semi-plano direito, podemos concluir que quando K é máximo, os pólos
estarão sobre o eixo imaginário.
Ponto para o valor
máximo de K
Região
Estável
Parte Imaginária
Montando uma equação com qualquer uma das linhas
da tabela de Routh e substituindo o valor de K para 9,65
Os neste exemplo), podemos encontrar s:
(valor máximo
Linha 2: 7 s 3  8  K s  0
ou
2
Linha 3: 90  K .s  21K  0
Região
Instável
Parte Real
90  9,65s 2  21 9,65  0
80,35s 2  202,7  0
s1, 2  0  j1,59
Prof. Marcio Kimpara
Ponto
cruzamento
33
Exemplos
R(s)
+
C(s)
K
G(s)
1
a)

s  2s  6
G( s) 
b)

s
G( s) 
Os
s 2  8s  25

 4s  20
s  2s  4
2
Resolvido no quadro!
Prof. Marcio Kimpara
34
Exemplo
R(s)
+
s  5
ss  1s  4
K
C(s)
-
Root Locus
15
1
Plote o lugar das raízes do sistema
acima utilizando o Matlab
Os
No Matlab:
G = tf( {[1 5]} , {[1 5 4 0]})  comando
para escrever a função de transf.
rlocus(G)  comando para plotar o lugar
das raízes.
Imaginary Axis
10
5
0
-5
-10
-15
-6
Prof. Marcio Kimpara
-5
-4
-3
-2
Real Axis
-1
0
35
1