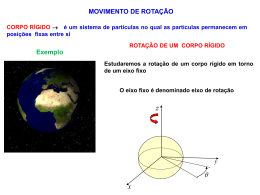
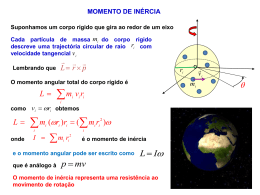
A Figura mostra as velocidades translacionais dos vários pontos sobre o cilindro
Observe que a velocidade translacional
(velocidade linear) de cada ponto do cilindro
está numa direcção perpendicular à linha
que une esse ponto ao ponto de contacto
O ponto P’ desloca-se com uma velocidade
v  2vCM
ENERGIA CINÉTICA DE ROLAMENTO
É a soma da energia cinética de
rotação em torno do CM com a
energia cinética associada ao
movimento de translação do CM.
1
1
2
2
K 
I CM   M vCM
2
2
COMBINAÇÃO DO MOVIMENTO DE TRANSLAÇÃO E ROTAÇÃO
Translação pura
Rotação pura

vCM

vCM

vCM
v  vCM  R
Translação + Rotação

2 vCM
v R

v 0
=
v  R
v   R  acima do centro
v    R  abaixo do centro

vCM
v 0
O ponto de contacto está sempre
em repouso
FOTOGRAFIA DE UMA RODA EM ROLAMENTO
Os raios de cima estão menos nítidos que os de baixo porque estão se
movendo mais depressa
Rolamento sobre um plano inclinado
Exemplo 1
Na direção y:
N  Mg cos  0
(1)
Na direção x:
Mg sin   Fa  MaCM
(2)

vCM
A força de atrito produz um momento da força (MO) em
relação ao CM:
M O  Fa R  I CM
(3)
Da condição de rolamento sem deslizamento: aCM  R

aCM

R
Tiro o valor de
Fa
em (3):

N
y

vCM
(4)
x
Fa  I CM aCM /R
Substituindo em (2) a fica:
I
Mg sin   CM2 aCM  MaCM
R
2

Fa
Mg cos
Mg sin



Mg
Exemplo 1 (continuação)
aCM
Mg sin 

 g sin 
I CM
M 2
R
1 / 2
M


 2 / 3
I
M  CM2 5 / 7
R
Temos ainda :
Fa 

N
y

vCM
e
x

Fa
Mg sin
Mg cos
anel

Mg
cilindro
esfera
I CM
I CM Mg sin 
Mg sin 
a


CM
2
2
2
MR 2
R
M  ( I CM / R ) R
1
I CM
À medida que aumenta a inclinação do plano a força de atrito estático necessária para
evitar o deslizamento vai aumentando. No limite, antes do deslizamento, temos Fa  Fe max
assim
Fa  Fe max   e Mg cos 
MR 2
tan    e (
 1 )  tan  r
I CM
Mg sin 
  e Mg cos
MR 2
1
I CM
r
e
 ângulo máximo (limiar) para
que haja rolamento sem deslizamento
ROTAÇÃO EM TORNO DE UM EIXO FIXO
Tabela de equivalências
Rotação em torno de um eixo fixo
Energia cinética
Equilíbrio
2a
lei de Newton
2a lei de Newton
Momento
Conservação
Potência
1
KR I2
2
Movimento de translação
1
K  mv 2
2
 
M 0
f 0


M  I


f ma
 
L I
 
Li L f
P  M


p mv
 
p i p f

 dL
M
dt
Momento de inércia
 dp
f 
dt
P F v
I
massa
m