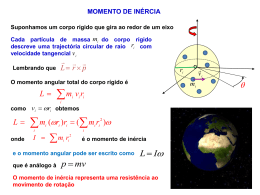
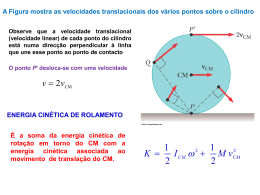
Física Geral I - F -128
Aula 13
Conservação do Momento
Angular e Rolamento
20 semestre, 2010
Conservação do momento angular
No sistema homem - halteres só há forças internas e, portanto:
L( z ) = Iω = constante ⇒
ω i Ii
I iω i = I f ω
f
ω f If
Com a aproximação dos halteres ( I f < I i ) a velocidade angular
do sistema aumenta.
Exemplo 3:
Conservação do momento angular
Dados
I bic = 1, 2 kg.m 2 ; I tot = 6,8 kg.m 2 e ω i = 3,9 rot/s
Queremos calcular a velocidade angular
final do sistema após o menino inverter o
eixo de rotação da roda de bicicleta (ver
figura)
Momento angular inicial do sistema
roda de bicicleta-menino (+ banco)
Li = Lbic = I bicω i
O menino inverte o eixo de rotação
da roda de bicicleta
Lbic → − Li
Exemplo 3:
Momento angular final do sistema:
L f = Lbic + Lmen = Lmen − Li
Conservação do momento angular
(pois só há forças internas no sistema)
L f = Li ⇒ Lmen − Li = Li
⇒ Lmen = 2 Li
I tot ω = 2 I bic ω
i
2 I bic ω i
ω =
≅ 1,4 rot/s
I tot
Conservação do momento angular
No caso da mergulhadora da figura ao lado o CM segue um
movimento parabólico.
Nenhum torque externo atua sobre ela em relação a um eixo que
passa pelo CM; então no referencial do CM:

dL ′
=
dt
∑
i
 
ri ′ × Fi =

LL′ ′
 
∑ mi ri ′ × g = 0
i


⊗
=0

e o momento angular L ′ da nadadora é constante
durante o salto. Juntando braços e pernas, ela
pode aumentar sua velocidade angular em torno
do eixo que passa pelo CM, às custas da redução
do momento de inércia em relação a este eixo.

Mg
Mg
Rolamento (sem deslizamento)
 O deslocamento
do centro de massa e a rotação estão vinculados:
 s é o deslocamento do centro de massa do objeto
 θ é o deslocamento angular do objeto em torno de um eixo que
passa pelo CM do sistema.
vCM
R
θ
s
s= Rθ
A velocidade do CM é dada por:
vCM =
ds dθ
= R = Rω
dt
dt
Rolamento (sem deslizamento)
Decomposição do rolamento em rotação + translação
Rotação
pura
Translação
pura

vCM

vCM

vCM
v = vCM = Rω
Translação
+ Rotação

2 vCM
v= ω R
+
v= 0
=
v= − ω R
v = rω (acima do centro)
v = − rω (abaixo do centro)

vCM
v= 0
O ponto de contato está
sempre em repouso
Rolamento (sem deslizamento)
Fotografia de uma roda em rolamento

2 vCM

vCM
v= 0
Figura da esquerda: o rolamento sem deslizamento pode ser descrito como uma
rotação pura com a mesma velocidade angular ω em torno de um eixo que sempre
passa pelo ponto P de contacto (eixo instantâneo de rotação).
De fato: v P′ = ω 2 R = 2 ω R = 2vCM
Figura da direita: os raios de cima estão menos nítidos que os de baixo porque
estão se movendo mais depressa.
Energia Cinética de Rolamento
Encarando o rolamento sem deslizamento como uma rotação pura
em torno do eixo instantâneo:
1
K= IPω 2
2
2
Mas I P = I CM + M R (teorema dos eixos paralelos)

2v
Então:
CM
1
1
2
K = I CM ω + M R 2 ω
2
2
1
1
2
2
K = I CM ω + M vCM
2
2
2
Isto é, a energia cinética do corpo rígido é a
soma da energia cinética de rotação em torno do
CM com a energia cinética associada ao movimento
de translação do CM.

vCM
v= 0
Exemplo 4:
O iô-iô
Torque externo relativo ao CM quando
o iô-iô desce:
r
T
Tr= I CM α
Dinâmica linear (eixo orientado para baixo)
Mg
Mg − T = Ma
Condição de rolamento:
Mg
T=
Mr 2
1+
I CM
v= ω r ⇒
e
a= α r
r2
a=
T=
I CM
g
I CM
1+
Mr 2
Exemplo 4:
Note que se o iô-iô sobe, o torque muda
de sinal
− Tr= I CM α
r
T
Por outro lado, o fio se enrola e a
condição de rolamento também muda
de sinal
v= − ω r ⇒
a= − α r
Mg
Ao final, as equações não mudam!
T r = − I CM α = I CM
Ma = Mg − T
a
r
Mg
T=
Mr 2
1+
I CM
r2
e a=
T=
I CM
g
I CM
1+
Mr 2
Exemplo 4:
Podemos ainda resolver o mesmo problema
usando a conservação de energia:
1 2 1
MvCM + I CM ω 2 = M g z
2
2
A condição de rolamento é
vCM = ω r
2gz
vCM = ±
= ± 2a z
I CM
1+
Mr2
r
Z
T
Mg
Sinal (+) para a descida e (–) para a subida.
Equação de Torricelli com aceleração constante dada por
g
a=
I CM
1+
Mρ 2
Rolamento (sem deslizamento)
Atrito no rolamento

ω
ω

⊗ ττ

Fa

Mg
Transforma
energia cinética
de translação em
rotação
Transforma
energia cinética
de rotação em
translação

ω
ω

τ
⊗ τ
Corpo rolando ladeira
abaixo devido ao próprio
peso.

FFaa

M
g
Mg
Roda de um carro girando.
Exemplo 5:
Rolamento sobre um plano inclinado
Na direção y:
N − Mg cos θ = 0
Na direção x:

vCM
Mgsen θ − Fa = Ma
Torque relativo ao CM:
Fa R = I CM α
Condição de rolamento sem
deslizamento: a = Rα
I CM = Mk 2
Momento de inércia:
( k é o raio de giração)

N
y

vCM
x

Fa
Mgcos θ
Mgsen θ

Mg
Exemplo 5:
g sin θ
a=
k2
1+ 2
R
 1/ 2
1

=
 2/3
2
k
1 + 2  5 / 7
R

N
y
e

vCM
x

Fa
anel
cilindro
Mgcos θ
Mgsen θ

Mg
esfera
Temos ainda:
k2
Fa = Mgsenθ 2 2
k +R
k 2 + R2
tgθ ≤ µ e
≡ tg θ
2
k
como
r
Fa ≤ Fe max = µ e Mgcosθ
Ângulo máximo (limiar) para que
haja rolamento sem deslizamento
Precessão do momento angular
Pião

L
Módulo do torque da força peso:
θ
τ = Mgr senθ

N
Lei fundamental da dinâmica das rotações:
 
∆L= τ ∆t

Mg
∆ L= Mg r senθ ∆ t
Da figura temos:
∆ L= L senθ ∆ ϕ = Iω senθ ∆ ϕ ∴
Mgr senθ ∆ t = Iω senθ ∆ ϕ
Velocidade angular de precessão:
∆ϕ
dϕ Mgr
Ω ≡
=
dt
Iω

τ
Precessão do momento angular
O centro de massa do pião executa
movimento circular com uma
aceleração centrípeta

L
θ
a c = Ω 2 r senθ

N
A força de atrito pião-piso é a
responsável por esta aceleração

Mg
Fa = MΩ 2 r senθ
Como
µg
senθ ≤ 2
Ω r
Fa ≤ µ Mg
para que a ponta do pião
fique fixa e haja apenas
movimento de rotação!
∆ϕ

Fa

τ
Um giroscópio

L

Mg

N
Precessão do momento angular
Como a Terra é um esferóide oblato (achatado nos polos), a Lua e
o Sol provocam forças como as mostradas abaixo e em 13.000 anos o
eixo de rotação sofre precessão de meio período, como na figura.