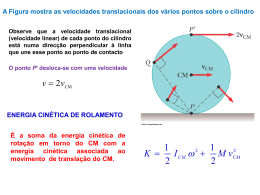
Módulo 6 – Rolamento e corpos rígidos
Objetivo: Estudar o movimento de rotação de um corpo
rígido em torno de um eixo móvel
Movimento mais geral de um corpo rígido é a combinação da
translação do centro de massa com a rotação em torno de um eixo
que passa pelo centro de massa
Energia cinética de um corpo rígido:
K
Energia cinética
de translação
1
1
MV cm2  I cm 2
2
2
Energia cinética
de rotação
Rolamento sem deslizamento:
Ponto de contato com a superfície deve permanecer instantaneamente
em repouso. Isto impõe a condição:
Vcm  R
Sistema: esfera metálica que desce uma canaleta rolando
sem deslizar
D
2R
h
R
d
v
h
H
H
2d
r
2d
A
A
Parâmetros físicos:
• A: alcance
• h: altura do movimento de rolamento
• H: altura da queda livre
• R: raio da esfera
• 2d: largura da canaleta
• v: velocidade de lançamento
• r: raio do movimento de rolamento: v=ωr
Cálculo do alcance - divide-se o movimento em duas
etapas: rolamento e queda livre
D
2R
h
R
d
v
h
H
H
r 2  R2  d 2
r
2d
2d
A
A
 A  vt
1 A2
2 Hv2

Queda livre: 
1 2 H  g 2  A
2 v
g
H  gt

2

Rolamento: conservação da energia
mgh 
Momento de inércia da esfera em relação a
um eixo que passa pelo centro de massa:
Rolamento sem deslizamento:
1 2 1 2 v2
gh  v  R 2
2
5
r
2 gh
v2 
 A
2
 2R 
1 

2 
 5 r 
1 2 1 2
mv  I
2
2
I
2
mR 2
5
v  r
4 Hh
4 Hh
2

A

teo
 2 R2 
 2 R2 
1 

1 

2 
2 
 5 r 
 5 r 
Inicialmente, vamos aprender a medir R e d com o paquímetro. As
incertezas destas medidas são muito menores que as incertezas das
medidas de H e h, realizadas com uma régua.
Incerteza de A (teórica):
A2 
4 Hh
 2 R2 
1 

2 
 5r 
4
 H 
2
2  h 
 A  2 AA 
 Hh  A    

2
 2R 
 h  H 
1 

2 
 5 r 
2
 
Ateo  h   H 
  

2  h  H 
2
Ateo 
2
2
Atividade I – Medir o alcance para 3 esferas de
diâmetros diferentes, soltando-as de uma altura h fixa,
comparando os resultados experimentais com as
previsões teóricas
R (cm)
A exp(cm) δA exp(cm)
A teo(cm)
(fim da primeira aula)
δA teo(cm)
Atividade II – Usando uma das esferas, medir o alcance
para 5 alturas h diferentes, obtendo o coeficiente
angular da reta A2 x h e comparando o resultado
experimental com as previsão teórica
A2 
4 Hh
 2 R2 
1 

2 
 5r 
Coeficiente angular:
Incerteza:
4H
 2 R2 
1 

2 
 5r 
4
H
2
 2R 
1 

2 
 5r 