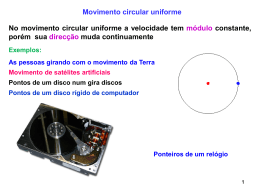
Exemplos de MCU 1 No movimento circular uniforme (MCU) Vector posição r r cos e x r sin ey Vector velocidade v r sin e x r cos ey 2 Movimento circular uniformemente variado No movimento circular uniformemente variado, a velocidade linear Como v r , a velocidade angular também não é constante. d d r cos e x r sin ey dt dt r r sin e x r cos ey onde at não é constante. dv d a r sin e x r cos e y dt dt A aceleração é 2 v d dt d r sin e x r cos e y dt é a aceleração angular a ac at v at ac é a aceleração tangencial e tem a mesma direcção do vector velocidade v at r 3 at a Módulo da aceleração total ac a a ac2 at2 Quando a aceleração angular é constante podemos obter const 0 t 1 2 0 0 t t 2 4 1.3 Movimento em três dimensões Para um movimento em três dimensões o vector posição é r xex ye y zez A velocidade média é v vmx ex vmy e y vmz ez A velocidade é v v x ex v y e y v z ez z A aceleração média é a amx ex amy e y amz ez ez ex A aceleração é a a x ex a y e y a z ez x ey r y 5
Baixar