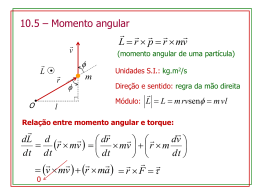
MOMENTO DE INÉRCIA
Suponhamos um corpo rígido que gira ao redor de um eixo
Cada partícula de massa mi do corpo rígido
descreve uma trajectória circular de raio ri com
velocidade tangencial v i
Lembrando que
  
L r p
ri
O momento angular total do corpo rígido é
L
mi
m v r
i
i i
i
como vi  ri obtemos
L
2
m
(

r
)
r

(
m
r
 i i i  i i )
i
onde
I 
m r
i
i
i
2
é o momento de inércia
e o momento angular pode ser escrito como
que é análogo à
p  mv
o
vi
L  I
O momento de inércia representa uma resistência ao
movimento de rotação

CONSERVAÇÃO DO MOMENTO ANGULAR
Quando

 dL  

M
 r  f  0  L  constante
dt


se
f  0 ou
r 0

M 0
ou

L  constante


Li  L f
Análogo ao que acontece com o momento linear
 
pi  p f
PARA QUE O MOMENTO DA FORÇA SEJA NULO NÃO É PRECISO QUE A FORÇA SEJA
NULA, QUANDO A FORÇA É COLINEAR COM O VECTOR POSIÇÃO TEREMOS TAMBÉM

M 0
Exemplo:
FORÇAS CENTRAIS, que são forças da forma
 

F (r )  f (r ) u
Neste caso:

 dL 

M
 r  f (r )u  0
dt

 L  constante
EXEMPLO 1: CONSERVAÇÃO DO MOMENTO ANGULAR
No sistema homem - halteres só há forças internas e, portanto:
L  I  constante

f I f
i I i
Com a aproximação dos halteres (
I i i  I f  f
If
<
Ii
) a velocidade angular do sistema aumenta
EXEMPLO 2: CONSERVAÇÃO DO MOMENTO ANGULAR
Queremos calcular a velocidade angular final do sistema após o menino
inverter o eixo de rotação da roda de bicicleta
Dados
Ibic  1, 2 kg.m2 ; Itot  6,8 kg.m2 e i  3,9 rot/s
Momento angular inicial do sistema
bicicleta-menino (+ banco)
roda de
Li  Lbic  I bici
Agora o menino inverte o eixo de rotação da
roda de bicicleta
Lbic   Li
EXEMPLO 2 (cont): CONSERVAÇÃO DO MOMENTO ANGULAR
Momento angular final do sistema:
L f  Lbic  Lmen  Lmen  Li
Há conservação do momento angular 
uma vez que só há forças internas no
sistema
L f  Li  Lmen  Li  Li
 Lmen  2 Li
I tot  2I bici
2 I bic i
 
 1,4
I tot
rot/s
Exemplo 3: CONSERVAÇÃO DO MOMENTO ANGULAR
No caso da mergulhadora da figura ao lado o CM segue um movimento parabólico
Nenhum momento da força externo em relação a um eixo que passa pelo CM , actua
sobre a mergulhadora; então no referencial do CM:
onde

 
 
dL 
  ri   Fi   mi ri   g  0
dt
i
i


=0

I   mi ri 
i


dL

 0  L  const.
dt

L
e o momento angular
da nadadora é constante
durante o salto. Juntando braços e pernas, ela pode
aumentar sua velocidade angular em torno do eixo
que passa pelo CM, às custas da redução do momento
de inércia em relação a este eixo

LL


Mg
Mg
QUANDO O MOMENTO ANGULAR VARIA COM O TEMPO
dL d
d
 ( I )  I
 I
dt dt
dt
ou


M  I
que é semelhante à equação de Newton


F  ma
ROLAMENTO (SEM DESLIZAMENTO)
Decomposição do rolamento em rotação + translação
Rotação pura
Translação pura

vCM

vCM

vCM
v  vCM  R
Translação + Rotação

2 vCM
v  R

v 0
=
v R
v  r (acima do centro)
v  r (abaixo do centro)

vCM
v 0
O ponto de contato está sempre
em repouso
FOTOGRAFIA DE UMA RODA EM ROLAMENTO
Os raios de cima estão menos nítidos
que os de baixo porque estão se
movendo mais depressa
ENERGIA CINÉTICA DE ROLAMENTO
É a soma da energia cinética de
rotação em torno do CM com a
energia cinética associada ao
movimento de translação do CM.
1
1
2
2
K 
I CM   M vCM
2
2