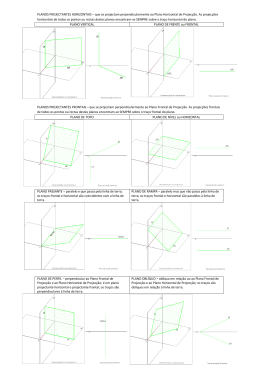
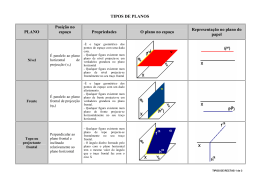
GEOMETRIA DESCRITIVA A
10.º Ano
Posição de um Plano em Relação aos
Planos de Projecção
© antónio de campos, 2009
ALFABETO DO PLANO
O alfabeto do plano é a classificação dos planos, em função das posições que
podem ter no espaço em relação aos planos de projecção.
Um plano projectante é um plano que projecta todos os seus pontos e rectas
sobre um plano de projecção.
PLANOS ORTOGONAIS AO
PLANO HORIZONTAL DE PROJECÇÃO
Planos Projectantes Horizontais
Plano Vertical
Plano ortogonal ao Plano Horizontal de Projecção (xy) e oblíquo ao Plano Frontal de
Projecção (xz).
xz
fα
α
fα
x
x
hα
xy
hα
Plano Frontal (ou de frente)
Plano ortogonal ao Plano Horizontal de Projecção (xy) e paralelo ao Plano Frontal de
Projecção (xz). É o único tipo de plano que contém rectas frontais com direcções
diferentes. Não tem traço frontal, por isso, o traço horizontal é representado
entre parêntesis, (hφ).
xz
φ
x
x
(hφ)
xy
(hφ)
PLANOS ORTOGONAIS AO
PLANO FRONTAL DE PROJECÇÃO
Planos Projectantes Frontais
Plano Horizontal (ou de nível)
Plano paralelo ao Plano Horizontal de Projecção (xy) e ortogonal ao Plano Frontal de
Projecção (xz). É o único tipo de plano que contém rectas horizontais com direcções
diferentes. Não tem traço horizontal, por isso, o traço frontal é representado
entre parêntesis, (fυ).
xz
(fυ)
(fυ)
υ
x
x
xy
Plano de Topo
Plano oblíquo ao Plano Horizontal de Projecção (xy) e ortogonal ao Plano Frontal de
Projecção (xz).
xz
fδ
fδ
δ
x
x
hδ
xy
hδ
PLANOS ORTOGONAIS AO
PLANO HORIZONTAL DE PROJECÇÃO
E AO PLANO FRONTAL DE PROJECÇÃO
Planos Duplamente Projectantes
Plano de Perfil
Plano ortogonal a ambos os planos de projecção, sendo duplamente projectante.
xz
fπ ≡ hπ
fπ
π
x
x
hπ
xy
PLANOS OBLÍQUOS AO
PLANO HORIZONTAL DE PROJECÇÃO
E AO PLANO FRONTAL DE PROJECÇÃO
Planos Não Projectantes
Plano Oblíquo
Plano oblíquo a ambos os planos de projecção, sendo não projectante.
xz
fα
fα
α
x
x
hα
xy
hα
Plano de Rampa
Plano oblíquo a ambos os planos de projecção, sendo não projectante. Os seus
traços frontais e horizontais são rectas fronto-horizontais.
xz
fρ
fρ
x
ρ
x
hρ
xy
hρ
Plano Passante
Plano oblíquo a ambos os planos de projecção, sendo não projectante. Os seus traços
frontais e horizontais são rectas fronto-horizontais coincidentes no eixo x. É um
caso particular dos planos de rampa, que contém o eixo x. É o único tipo de plano que
necessita de um ponto para ser completamente definido, para além dos traços do
plano.
xz
A2
A2
A
x ≡ fρ ≡ hρ
ρ
A1
xy
x ≡fρ ≡ hρ
A1
Um plano de rampa ρ tem o fρ com 4 cm de cota e hρ com 3 cm de afastamento.
O plano ρ contém uma recta fronto-horizontal g, com 3 cm de cota. Desenha as
projecções da recta g.
fρ
F2
g2
P2
H2
x
g1
P1
H1
hρ
F1
r1
r2
Um plano frontal φ com 3 cm de afastamento, contém um triângulo [ABC]. O
ponto A tem 1 cm de cota. B tem 4 cm de cota e situa-se à direita de A. A0B0 =
3 cm. C tem 0 cm de cota e situa-se à direita de B. B0C0 = 1 cm. Desenha as
projecções do triângulo [ABC].
B2
A2
x
(hφ)
A0
B0
C0 ≡ C2
A1
B1
C1
Um plano horizontal υ com 3 cm de cota, contém um triângulo [ABC]. O triângulo
está situado no 1.º diedro. O ponto A tem 2 cm de afastamento. [AB] mede 5 cm
e está contido numa recta horizontal que faz um ângulo de 30º (a.d.) com o Plano
Frontal de Projecção. [BC] está contido numa recta de topo. C tem afastamento
nulo. Desenha as projecções do triângulo [ABC].
(fυ) ≡ h2
B2 ≡ (t2) ≡ C2
A2
C1
x
t1
A1
h1
B1
Um plano de perfil π contém um triângulo [JKL], sendo J (1; 1), K (4; 2) e L (3;
4). Desenha as projecções do triângulo [JKL].
fπ ≡ hπ
L2
K2
J2
x
J1
L1
K1