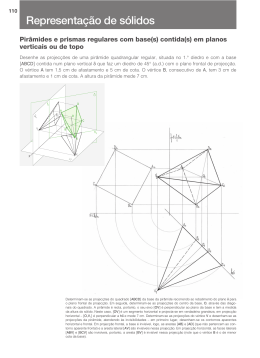
GEOMETRIA DESCRITIVA A
10.º Ano
Sólidos II
© antónio de campos, 2010
GENERALIDADES
Para os casos em que um sólido está contido num plano projectante não
paralelo aos planos de projecção, é necessário a utilização de um método
geométrico auxiliar para resolver situações como obter as projecções do
sólido, via a V.G. da base.
Qualquer dos três métodos (mudança do diedro de projecção, rotação ou
rebatimento) pode ser utilizado para resolver estas situações. O método de
rebatimento é o mais fácil e simples para estas situações.
Projecção de
Sólidos com
Bases Verticais
Os pontos A (0; 1) e B
(2,5; 0) são vértices
consecutivos de um
quadrado [ABCD],
contido num plano
vertical, que faz um
diedro de 45º (a.d.)
com o Plano Frontal
de Projecção.
O quadrado [ABCD] é
a base de uma
pirâmide
quadrangular regular,
com 5 cm de altura e
situada no 1.º diedro.
Desenha as
projecções da
pirâmide.
fα ≡ e2 ≡ fαr
Dr
D2
C2
Cr
Vr ≡ Qr
V2
Q2
A2≡ Ar
x ≡ hαr
A1 ≡ (e1)
Br
B2
D1
Q1
B1
C1
V1
hα
É dado um plano
vertical α que faz um
diedro de 45º (a.d.)
com o Plano Frontal
de Projecção.
Os pontos A (3; 0) e
D (2; 6) pertencem
ao plano α e são dois
extremos de uma
das diagonais
maiores de um
hexágono regular
[ABCDEF], contido
no plano α.
fα ≡ e2 ≡ fαr
Dr
Cr
C2
Er E2
Vr ≡Or
V2
O2
B2
Br
Fr
x ≡ hαr
Ar
F2
(e1)
E1
F1
A2
D1
O hexágono é a base
de uma pirâmide
hexagonal regular,
com 7 cm de altura e
situada no 1.º diedro.
Desenha as
projecções da
pirâmide.
D2
O1
A1
C1
V1
B1
hα
São dados dois
pontos A (1; 0;
4) e B (-1; 1; 0),
que são dois
vértices
consecutivos de
um quadrado
[ABCD], contido
num plano
vertical.
O quadrado
[ABCD] é uma
das bases de um
prisma
quadrangular
regular, situado
no 1.º diedro e
com 6 cm de
altura.
Desenha as
projecções do
prisma.
y≡ z
fδ ≡ e2 ≡ fδr
Dr
D’2
D2
A2 ≡ Ar
A’2
C’2
Cr
Br
x ≡ hδr
B’2
A1 ≡ (e1)
C2
B2
B1
D1
C1
hδ
A’1
B’1
D’1
C’1
(hδ1)
Os pontos A (2; 2)
e B (5; 4) são dois
vértices de um
triângulo
equilátero [ABC],
existente num
plano vertical α.
O plano α faz um
diedro de 45º
(a.d.) com o Plano
Frontal de
Projecção.
O triângulo [ABC]
é uma das bases
de um prisma
triangular regular,
com 6 cm de altura
e existente no 1.º
diedro.
Desenha as
projecções do
prisma.
fα ≡ e2 ≡ fαr
C’2
Cr
C2
B’2
B2
Br
Ar
A2
A’2
(e1)
x ≡ hαr
A1
C1
B1
A’1
C’1
hα
hα ’
B’1
(hα1)
É dada uma pirâmide
quadrangular regular,
situada no 1.º diedro,
com 7 cm de altura e
com a base contida
num plano vertical γ,
que faz um diedro de
30º (a.d.) com o Plano
Frontal de Projecção.
A base da pirâmide é
o quadrado [ABCD],
que tem 4,5 cm de
lado.
fγ ≡ e2 ≡ fγr
C2
Cr
D2
Dr
Or
V2
Br ≡ B
2
x ≡ hγr
(e1) ≡ B1
Ar
C1
O vértice A tem 2cm
de afastamento e
cota nula.
A2
O1
A1
D1
O vértice B tem
afastamento nulo e é
consecutivo a A.
Desenha as
projecções da
pirâmide.
O2
hγ
V1
Projecção de
Sólidos com
Bases deTopo
fγ1
C’2
É dado um cubo com
3 cm de aresta,
situado no 1.º diedro.
Uma das faces do
cubo é o quadrado
[ABCD], contido num
plano de topo γ, que
faz um diedro de
40º (a.d.) com o
Plano Horizontal de
Projecção.
O lado [AB] está
contido numa recta
passante r, sendo A
(1; 2).
Desenha as
projecções do cubo.
D’2
B’2
fγ ≡ r 2
A’2
B2
C2
A2
D2
(e2)
x≡
fγr
rr
A’1
Ar
A1
Br
Dr
Cr
D’1
B’1
B1
r1
D1
C’1
hγ≡ e1 ≡ hγr
C1
É dada uma
pirâmide
hexagonal
regular,
situada no 1.º
diedro, com 7
cm de altura e
com a base
contida num
plano de topo
α.
Os pontos A (1; 1; 1) e B (-4;
0; 3) são dois
vértices
consecutivos
do hexágono
[ABCDEF] da
base.
Desenha as
projecções da
pirâmide.
y≡ z
V2
D2
E2
(e2) F2
Br
x ≡ fαr
O2
C2
B2
A2
B1
Ar
A1
C1
Cr
V1
Or
Fr
Dr
O1
F1
D1
hα ≡ e1 ≡ hαr
Er
E1
fα
É dado um prisma
quadrangular
regular, situada no
1.º diedro, com 7 cm
de altura e com as
bases contidas em
planos de topo, que
fazem diedros de
35º (a.e.) com o Plano
Horizontal de
Projecção.
A base inferior é o
quadrado [ABCD],
que tem 4,5 cm de
lado.
O ponto A tem cota
nula e 4 cm de
afastamento, e o
ponto B tem 2 cm de
afastamento.
Desenha as
projecções do
prisma.
C’2
(fθ’)
B’2
D’2
fθ
A’2
C2
B2
D2
A2 ≡ (e2)
x ≡ fθr
B1
B’1
Br
A1 ≡ Ar
C1
A’1
Cr
C’1
hθ≡ e1 ≡ hθr
D1
Dr
D’1
É dada uma pirâmide
quadrangular regular,
situada no 1.º diedro,
com 10 cm de altura e
com a base contida num
plano de topo θ.
A base é o quadrado
[ABCD], que se inscreve
numa circunferência
com 4 cm de raio, cujo
centro tem 4 cm de
cota.
O vértice A do
quadrado, tem 2 cm de
cota e afastamento
nulo.
O plano θ faz um diedro
de 60º (a.d.) com o
Plano Horizontal de
Projecção.
Desenha as projecções
da pirâmide.
V2
fθ
D2
C2
O2
B2
x ≡ fθr
(e2)
Ar
Dr
V1
A1
D1
O1
Or
Br
Cr
A2
B1
C1
hθ≡ e1 ≡ hθr
É dado um prisma
hexagonal regular,
situada no 1.º diedro,
cujas faces laterais são
quadrados.
O hexágono regular
[ABCDEF] é a base
inferior do prisma,
contida num plano de topo
θ, que faz um diedro de
45º (a.d.) com o Plano
Horizontal de Projecção.
C’2
Desenha as projecções do
prisma.
(fθ’)
fθ
E’2
D2
B’2
A’2
C2
F’2
E2
B2
F2
B’1
Br
Cr
B1
A2 ≡ (e2)
x ≡ fθr
O vértice A do hexágono,
tem 2,5 cm de
afastamento e cota nula.
O vértice B do hexágono,
tem afastamento nulo, e o
lado [AB] tem as suas
projecções paralelas
entre si.
D’2
A’1
A1 ≡ Ar
C’1
Dr
F’1
Er
C1
D1
D’1
Fr F1
E’1
hθ≡ e1 ≡ hθr
E1
Projecção de Sólidos
com Bases de Perfil
fπ ≡ hπ≡ e2 ≡ fπr
É dada uma pirâmide
pentagonal regular com 5,5 cm
de altura, situada no 1.º diedro.
O pentágono [ABCDE] da base,
está contido num plano de
perfil e é circunscrita por uma
circunferência com 2,5 cm de
raio, sendo o centro o ponto Q
(3,5; 3).
A é o vértice com maior
afastamento da base.
x ≡ hπr
O lado [CD] é vertical e oposto
ao vértice A.
B é o vértice com maior cota
da base.
O vértice da pirâmide está à
direita da base.
Desenha as projecções da
pirâmide.
B2
Br
Cr
Ar
Qr
Q2 ≡ A 2
Dr
Er
C2
V2
D2
E2
(e1)
C1 ≡ D1
Q1
B1 ≡ E1
A1
V1
É dada uma
pirâmide
triangular
regular, situada
no 1.º diedro,
com 6 cm de
altura e com a
base contida
num plano de
perfil.
A (1; 3) e B (5;
2) são dois
vértices da
base.
O vértice da
pirâmide está à
esquerda da
base.
Desenha as
projecções da
pirâmide.
fπ ≡ hπ≡ e1 ≡ hπr
C2
V2
O2
A2
B2
(e2)
x ≡ fπr
Ar
A1
V1
O1
C1
B1
Or
Br
Cr
É dado um prisma
quadrangular
regular, situada no
1.º diedro, com
bases de perfil, e
com 6 cm de
altura.
C’2
B’2
A base mais à
direita é o
quadrado [ABCD],
sendo A (2; 1).
O lado [AB] do
quadrado faz um
ângulo de 60º com
o Plano Horizontal
de Projecção, e o
vértice B tem
afastamento nulo.
Desenha as
projecções do
prisma.
fπ ≡ hπ≡ e2 ≡ fπr
fα ≡ hα
C2
Br≡ B2
D’2
D2
A’2
A2
B’1
x ≡ hπr
Cr
Dr
Ar
(e1) ≡ B1
A’1
A1
C’1
C1
D’1
D1
É dado um prisma
quadrangular oblíquo,
situada no 1.º diedro, com
bases de perfil, e com 5
cm de altura.
B2
C’2
A base mais à direita é o
quadrado [ABCD], que se
inscreve numa
circunferência tangente ao
Plano Frontal de
Projecção, cujo centro é o
ponto O (3; 6).
O vértice A do quadrado,
tem 3,5 cm de cota e
afastamento superior a O.
O eixo do sólido tem as
suas projecções paralelas
entre si, e a sua projecção
frontal faz um ângulo de
30º (a.d.) com o eixo x.
Desenha as projecções do
prisma.
fπ ≡ hπ≡ e2 ≡ fπr
C2 Cr
fα ≡ hα
B’2
O2
Or
D2 Dr
A2
D’2
A’2
x ≡ hπr
(e1)
D1
C1
D’1
C’1
A’1
B’1
Br
O1
A1
B1
Ar