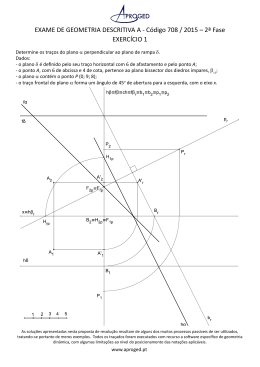
GEOMETRIA DESCRITIVA A
11.º Ano
Exame 2010 – 2.ª Fase
© antónio de campos, 2010
1.
Determine os
fα
traços do plano π
que contém o ponto
P e é paraleo ao
plano α.
y≡ z
b2
Dados
- o plano α é
definido pelas
retas a e b;
a2
F’’2
- a recta a contém
o ponto S (3; 5; 3);
- as projecções,
horizontal e
frontal, da recta a
fazem, com o eixo
x, ângulos de 45º,
de abertura para a
direita, e de 30º,
de abertura para a
esquerda,
respectivamente;
- a recta b
pertence ao plano
bissector dos
diedros impares,
(β1,3), e a sua
projecção frontal
faz, com o eixo x,
um ângulo de 30º
de abertura para a
direita;
- o plano π contém
o ponto P (-6; 3; -
fπ
Q2
H1
S2
x
b’2
a’2
F’’1
H2
H’’2 F1
F’1
H’2
F2
P1
Q1
P2
S1
hπ
F’2
H’1
a’1
a1
H’’1
b1
hα
b’1
2.
Determine
y≡ z
pr
graficamente a
amplitude do
ângulo formado
pelos planos δ e
θ.
fθ
p2
Dados
Ar
- o plano δ é
oblíquo e os seus
traços são
coincidentes nos
planos de
projecção;
- o traço
horizontal do
plano δ cruza o
eixo x num ponto
com 6 cm de
abcissa e faz um
ângulo de 60º, de
abertura para a
esquerda, com
esse mesmo eixo;
- o plano θ é de
topo e contém o
ponto R (-5; 6; 5)
e faz um diedro
de 50º, de
abertura para a
esquerda, com o
plano horizontal
de projecção.
p’2 ≡ e2 ≡ p’r
αº
R2
P2 ≡ Pr
Ar1
A2
x
p’1 ≡ (hφ) ≡ e1
f δ ≡ hδ
P1
p1
A1
R1
hθ
3.
Determina a sombra própria
y≡ z
e a sombra real de um prisma
pentagonal regular, nos planos de
projecção.
Ponha em destaque quer o
contorno da sombra real nos
planos de projecção, quer as
projecções do prisma.
f α ≡ hα
fπ ≡ hπ ≡ e1 ≡ hπr
E2
E’2
D2
D’2
Es2
E’s2
Identifique, a traço
interrompido, as linhas invisíveis,
quer no sólido, quer na parte
ocultada do contorno da sua
sombra projectada nos planos de
projecção.
O2 ≡ A2 ≡ As2
Identifique as áreas visíveis das
sombras própria e projectada,
preenchendo-as a tracejado ou
com uma mancha de grafite clara
e uniforme.
C2
C’2
B2
B’2
A1 ≡ (e2)
A’1
Ar
Nota – Se optar pelo tracejado, x ≡ fπr
deverá fazê-lo com linhas paralelas ao
eixo x, nas áreas de sombra própria, e
com linhas perpendiculares às
respectivas projecções de direcção
Er
luminosa, nas áreas de sombra
projectada.
Bs1
Br
Or
Dados
B’1 ≡ E’1
Cs1
C’s1
- as bases estão contidas em
planos de perfil;
- os pontos O (2; 4,5; 6) e o
ponto A (2; 0; 6) são,
respectivamente, o centro e um
dos vértices da base [ABCDE];
- o plano de perfil da outra base
tem –5 cm de abcissa;
- a direcção luminosa é a
convencional.
Dr
Cr
C1 ≡ D1
D’s2 D’v1
Bv2
B1 ≡ E1
O1
A’2
C’1 ≡ D’1
4.
Construa uma representação axonométrica ortogonal de uma forma tridimensional
composta por um prisma quadrangular regulare e por uma pirâmide triângular oblíqua de
base regular, de acordo com os dados abaixo apresentados.
Ponha em destaque, no desenho final, apenas o traçado das linhas visíveis do sólido
resultante.
Dados
Sistema axonométrico
-trimetria: a projecção axonométrica do eixo y faz ângulos de 130º e de 120º com as
projecções dos eixos x e z, respectivamente.
Nota - Considere os eixos orientados em sentido directo: o eixo z vertical, orientado positivamente de baixo para
cima, e o eixo x, orientado positivamente da direita para a esquerda.
Sólidos:
- os pontos R (5; 5; 11) e S (0; 5; 11) definem uma aresta comum.
Prisma quadrangular regular:
- uma base está situada no plano coordenado horizontal xy;
- os pontos R e S definem a aresta de maior afastamento da outra base.
Prisma quadrangular regular:
- a base [RST] é paralela ao plano coordenado horizontal xy, sendo T o ponto de maior
afastamento;
- o vértice da pirâmide coincide com o centro da face de maior afastamento do prisma.
z
z’r
zr
R3r ≡ S3r
T3r
S
R
T
Or
O’r
V
O
Or
y’r
O’r
x
yr
xr
y
S1r
x’r
yr
R1r
T1r
y’r