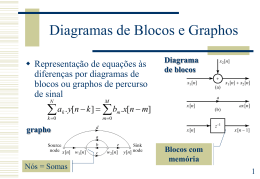
A Transformada-Z
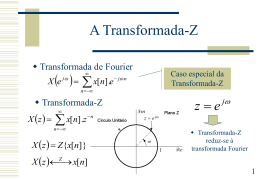
 Transformada de Fourier
    x[n].e
X e
j

n  
 Transformada-Z
X z  

n
x
[
n
].
z

n  
X z   Z{x[n]}
 j n
Caso especial da
Transformada-Z
ze
j
 Transformada-Z
reduz-se á
transformada Fourier
Z
X z  

x[n]
1
A Transformada-Z
 Transformada Z


Determinação de zeros e pólos
Analise de estabilidade de sistemas discretos
 Transformada de Fourier



Permite funções generalizadas (diracs)
Estudos de sistemas com entradas sinusoidais, por
exemplo modelação e desmodelação
Resposta em frequência de sistemas
2
Transformada-Z de uma
exponencial
X z  

 a u[k ] z
k
k  
a z   a z 
1  a z 
1  1
1 0
1

k


az 

k  
1  

 az
1  a z 1



1 0


k 0
Para a série ser absolutamente
somável devemos ter
1

1  a z 1
X z     a u[1  k ] z
k

  az
1  k
k
a z 1  1  z  a
1

   a z 1
1

1  a z 1

k

k  
Para a série ser absolutamente
somável devemos ter
a z 1  1  z  a
3
Região de Convergência (ROC)
 Region of Convergence
 Zona para a qual a série converge
(ROC)
 Corresponde sempre a um disco (sem as fronteiras)
 Quando contém o circulo unitário existe transformada de Fourier
1
0.5
0
-10
-5
Sequência direita
x[n]=0, n<n0
|z|>a
0
5
1
0.5
0
-10
10
1
0.5
0
-5
0
5
10
0
5
10
15
20
Sequência
bilateral
a<|z|<b
Sequência esquerda
x[n]=0, n>n0
|z|<a
4
Região de convergência
 Para a série convergir temos de ter

n
x
[
n
].
z


n  
Ou seja

 x[n] z
n  
n

Pelo que a região só depende do
módulo de z, e portanto
corresponde a discos centrados na
origem
5
Transformada-Z Racional
 Em muitos casos práticos podemos representar a
transformada-Z por uma função racional.
Corresponde aos casos em que x[n] pode
P( z )
X z  
ser expresso como uma soma de
Q( z )
exponenciais complexas
 Zeros de Q pólos da transformada, X(z)
 Zeros de P zeros da transformada
 A ROC não pode conter pólos, estando limitada
por estes.
6
Pólos e Zeros
Zeros
Os pólos
permitem
analisar a
estabilidade
do sistema
Pólos
O ROC está
limitada pelos
pólos!
7
Pólos e Zeros
pólo
pólo
H ( z) 
10
z  0.5
( z  0.5  0.5i )(z  0.5  0.5i )
8
Pólos:0.5-0.5i e 0.5+0.5i
6
4
Zero: -0.5
2
zero
0
-2
1
0.5
1
0.5
0
Real
0
-0.5
-0.5
-1
-1
Imaginário
Gráfico do valor
absoluto da
transformada-z de
uma função racional
8
Transformada-Z de Alguns Sinais
Sequência
Transformada
 [n]
1
a nu[n]
1
1  a.z 1
n
n.a u[n]
 a u[n 1]
n
 n.a u[n 1]
n
ROC
Pólo em ‘a’
a.z 1
za
1  a.z 
za
1
1  a.z 1
za
1 2
a.z 1
1  a.z 
1 2
Pólo duplo em ‘a’
za
 Consultar o Livro para uma tabela mais completa
9
Inversão da Transformada-Z
 Por Tabelas  (casos simples)
 Expansão em fracções parciais  (funções racionais)
M 1
A
i
k
H ( z 1 )  

a
z

k
1
k 1 1  d k .z
i 0
N
 Expansão em série  (polinómios)
 Resolução numérica da equação às diferenças
correspondente.
 Formula….
Nota: (não esquecer a ROC)
10
Inversão da Transformada-Z
 Expansão em fracções parciais  (funções racionais)
1
N
M 1
A
P
(
z
)
i
k
H ( z 1 ) 


a
z

 k
Q( z 1 ) k 1 1  d k .z 1 i 0
Pólos, dk simples e
distintos
Termo surge apenas
quando ordem de P é
maior que de Q
Cada um dos termos pode-se inverter
recorrendo a tabelas
11
Propriedades da Transformada-Z
 Linearidade
 Diferenciação de X(z)
Z
a1 x1[n]  a2 x2 [n] 
a1. X 1 ( z )  a2 . X 2 ( z )
dX ( z )
n x[n]   z
dz
ROC  RX
Z
ROC contémRx1  Rx2
 Deslocação no tempo
Z
x[n  n0 ] 
z  n0 X ( z )
ROC  RX
 Multiplicação por
exponencial
Z
z0n x[n] 
X ( z / z0 )
ROC  z0 RX
 Inversão no tempo
Z
x*[n] 
X * (1 / z * )
ROC  1 / RX
 Valor inicial
x[0]  lim(1  z 1 ) X ( z ),
z 
se x[n]  0, n  0
 Conjugação
Z
x*[n] 

X * ( z* )
 Convolução no
tempo
Z
x1[n] * x2 [n] 
X1 ( z) X 2 ( z)
ROC contémRx1  Rx2
12
Função de Sistema
 A transformada Z da resposta impulsiva de um
sistema designa-se por, função de sistema, H(z)
H ( z)  TZ h[n]
 A função de sistema é equivalente à função de
transferência quando Z se encontra no circulo
unitário.
j
H (e )  H ( z) z e j
13
Resolução de Equações às
Diferenças
N
M
 a . y[n  k ]   b
k 0
k
m 0
m
.x[n  m]
Função de
sistema
TZ
M
N
 ak . y ( z ) z
k 0
k
M
  bm x( z ).z
m 0
m
y( z)
 H ( z) 

x( z )
m
b
.
z
m
m 0
N
k
a
.
z
 k
k 0
14
Resolução de Equações às Diferenças
Para o caso de condições iniciais não nulas existe um regime transitório:
N
y[n]  yF [n]   a p z np
Num ponto do futuro
relativamente as condições
inicias (sistema causal)
p 0
Resposta
forçada
Regime transitório
(zp – pólos de H(z))
O regime transitório é formado por uma soma de exponências complexas de
bases que correspondem aos pólos do sistema, zp.
Os coeficientes da resposta ap podem ser obtidos atravez da resolução de um
sistema de equações obtido atravez da aplicação das condições iniciais do
sistema.
15
Regime transitório
Para ajudar a relembrar
 Temos que:



N
a
p 0
p
z
n
p
Y(z)=H(z) X(z)
Apenas pode existir sinal y para x(z)=0, se H(z)= ou
seja para os pólos de H(z)!!
Se o pólo estiver fora do circulo unitário a saída
cresce sem limites  sistema instável
16
Estabilidade
 Sistema causal e estável

Pólos dentro do circulo de raio
unitário
 Sistema de fase mínima (causal)



Sistema estável e de inversa causal e estável
Pólos e zeros dentro do circulo de raio unitário
Notar que a inversa de um sistema que não é de fase mínima
pode ser considerado como sistema não causal ou um sistema
instável dependendo da ROC escolhida.
17
Estabilidade
 A resposta impulsiva de um sistema estável tem transformada Z
 A ROC de um sistema estável contem o circulo unitário (tal
permite testar a estabilidade de sistemas causais e não causais)
Notar que: a resposta impulsiva de sistema causal é um sinal direito
e portanto a ROC é externa o que implica que os pólos devem
estar no interior do circulo unitário
18
Estabilidade
Sistemas estáveis
Sistemas instáveis
Sistema
causal
Circulo raio
unitário
ROC
19
Inversão de Sistemas
Sistema de fase mínima:
Sistema de fase não mínima:
Pólos e zeros dentro do
Circulo unitário
Zeros fora do Circulo unitário.
Não tem inversa
estável e causal.
Mas têm inversa não
causal e estável, ou
instável e causal….
São estáveis e causais e têm
inversa estável e causal
1
h[n]
Inversa
não
causal..
0.5
0
-10
-8
-6
-4
-2
0
2
4
6
8
10
20