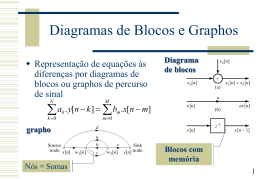
Diagramas de Blocos e Graphos
 Representação de equações às
diferenças por diagramas de
blocos ou graphos de percurso
de sinal
N
M
 a . y[n  k ]   b
k 0
k
m 0
m
Diagrama
de blocos
.x[n  m]
grapho
Blocos com
memória
Nós = Somas
1
Problemas Numéricos
 quantificação (arredondamentos ou truncagens
....)

Nos coeficientes do filtro
Pode tornar o sistema estável
 Modifica a resposta do sistema


Nos sinas

Produz ruído
Diferentes estruturas têm diferentes
comportamentos numéricos
2
Problemas Numéricos
Filtro Elíptico passa banda de ordem 12
Implementação em
cascata
Estrutura
directa
3
Ruído de Quantificação
 Normalmente é modelado por ruído branco com
uma distribuição uniforme, ou seja temos
Quantificador
x[n]
x[n]
y[n]
y[n]

 
12
2
Ruído - n[n]
com
2
n
Passo de quantificação
2
n
4
Filtros FIR
 Realização directa
Linha de atraso
Combinador linear
M
y[n]   bm .x[n  m]
m 0
Permite a utilização de um acumulador
de maior número de bits, reduzindo o
erro de quantificação a um
arredondamento final
5
Formas Transpostas
 Se trocarmos a entrada com a saída e invertermos as
direcções de todos os ramos de um grapho linear, a
função de transferência não se altera.
H1(z)
H1(z)
H2(z)
H2(z)
Daqui resultam as
formas transpostas
6
Realização transposta
Utilizando o teorema da transposição temos:
w0[n]
w1[n]
w2[n]
Esta implementação requer um arredondamento para cada coeficiente
conduzindo a maiores erros numéricos.
Wk+1[n]=Wk[n-1]+h[M-k] x[n]
7
Atraso de Grupo
 Assuma um sinal de banda base
s(n) de banda estreita, modelado
em amplitude, com portadora :
s[n] sin[n]

 Na saída de um SLIT o sinal será modificado resultando,
sn   A sinn   
Com
A  Abs[ H (e j )]
  arg[ H (e j )]
d
j
 ( )  
{arg[ H (e )]}
d
() é o atraso de grupo do filtro
Notar que  em real não é inteiro, pelo que escrever
s[n- ] é um abuso de notação.
8
Filtros FIR de Fase Linear
(Generalizada)
Resposta em
frequência:
j
j
H (e )  A(e ) e
 j (    )
=0  Fase
estritamente linear
Atraso de grupo constante  ( )   d {arg[ H (e j )]}  
d
(não há distorção de fase):
Tipo I
Tipo II
Tipo III
Tipo IV
0nM
h[n]  h[M  n], M par
h[n]  h[M  n], M impar
h[n]  h[M  n], M par
h[n]  h[M  n], M impar
d     M / 2
=/2
d – atraso de
grupo
(em amostras)
9
Implementação Directa Tipo I e II
Implementação
directa tipo I
N
(grafos)
M
 a . y[n  k ]   b .x[n  m]
k 0
Implementação
directa tipo II
k
m 0
m
a0  1
10
Formas Transpostas
 Se trocarmos a entrada com a saída e invertermos as
direcções de todos os ramos de um grapho linear, a
função de transferência não se altera.
H1(z)
H1(z)
H2(z)
H2(z)
Daqui resultam as
formas transpostas
11
Forma em Cascata
 Secções de segunda ordem
Em geral é sempre possível expressar um
dado filtro decomposto em pólos e zeros.
M1
H ( z)  A
 (1  f
k 1
M1
M2
k
z 1 ) (1  g k z 1 )(1  g k* z 1 )
k 1
M2
 (1  c z ) (1  d z
k 1
1
k
k 1
k
1
b0k  b1k z 1  b2k z 2
H ( z)  A
1
2
k 1 1  a1k z  a2 k z
N
Agrupar os pólos e zeros
complexos conjugados resulta em
secções reais de segunda ordem
)(1  d k* z 1 )
Pólos complexos conjugados
Pólos reais
12
Forma em Cascata
 Ordenação das secções

As secção mais selectivas devem aparecer no fim de forma a filtrar ao
máximo o ruído de quantificação.
 Emparelhamento de pólos com zeros

Emparelhar pólos e zeros próximos conduz a sistemas com menor gama
dinâmica, ou seja a relação entre o máximo e o mínimo da resposta em
frequência da secção, o que em geral reduz o ruído de quantificação.
13
Forma em Cascata
 Ganho de cada secção
 No caso de DSPs de virgula fixa o ganho de cada uma das secções deve ser
ajustado de forma a garantir que não se dá a saturação!!
 Para sinais de entrada limitados a amplitude máxima do sinal na saída é
dado pela soma do valore absoluto da resposta impulsiva. Tal pode ser
determinado na saída de cada secção.
 Em cada uma das secções (sem zeros) o sinal de entrada que conduz ao
maior nível na saída tem uma frequência que é dada pela frequência de
ressonância da secção. Este pode ser aproximado por um sinal sinusoidal.
Neste caso teremos que a secção deverá ter um ganho que é dado por 1/(1|p|) em que |p| a amplitude dos pólos da secção.
14
Forma Paralela
Np
N1
Ak

1
1

c
z
k 0
k
H ( z )   Ck z  
1
k 0
Bk (1  ek z 1 )

1
* 1
k 0 (1  d k z )(1  d k z )
N1
e0 k  e1k z 1
H ( z )   Ck z  
1
2
k 0
k 0 1  a1k z  a2 k z
Np
1
N1
Permite implementação paralela,
mas em geral conduz a um maior
ruído de quantificação, que é
simplesmente a soma do ruído de
cada secção!
15
Ciclos Limite
 Devido aos erros de quantificação pode existir saída
sem existir entrada!
1
0.5
0
-0.5
yˆ [ n]  Q[a yˆ[n  1]]  x[n]
-1
Resposta Impulsiva para a=(-3/4) e
palavras de três bits+sinal
Uma Solução:
arredondar em direcção
a zero. Mas tal aumenta
os erros de
arredondamento e não
elimina ciclos fora da
origem!
Outro
exemplo
a=(-3/4)
16