A Transformada-Z
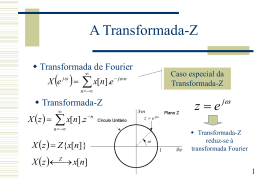
 Transformada de Fourier
    x[n].e
X e
j

n  
 Transformada-Z
X z  

n
x
[
n
].
z

n  
X z   Z{x[n]}
 j n
Caso especial da
Transformada-Z
ze
j
 Transformada-Z
reduz-se á
transformada Fourier
Z
X z  

x[n]
1
Transformada-Z de uma
exponencial
X z  

 a u[n] z
n
k  
a z   a z 
1  a z 
1  1
1 0
1

X z  
a z 
k
k  
1  

 az
1  a z 1



1 0

  a z 1

n

k 0
Para a série ser absolutamente
somável devemos ter
1

1  a z 1
 a u[1  n] z
n

k

a z 1  1  z  a
 a z 
1
1  n

k  
1

1  a z 1
Para a série ser absolutamente
somável devemos ter
a z 1  1  z  a
2
Região de Convergência (ROC)
 Zona para a qual a série converge  Region of Convergence (ROC)
 Corresponde sempre a um disco (sem as

A cinzento
n
fronteiras)
x[n].r  
 Quando contém o circulo unitário existe
n  
 É a região de
transformada de Fourier

1
0.5
0
-10
-5
0
Sequência direita
x[n]=0, n<n0
5
10
1
0.5
0
-10
convergência de uma
série de potências
-5
0
5
10
Sequência esquerda
x[n]=0, n>n0
Sequência
bilateral
3
Transformada-Z Racional
 Em muitos casos práticos podemos representar a
transformada-Z por uma função racional.
P( z )
X z  
Q( z )
 Zeros de Q pólos da transformada
 Zeros de P zeros da transformada
 A ROC não pode conter pólos, estando
limitada por estes.
Corresponde aos casos
em que x[n] pode ser
expresso como uma soma
de exponenciais
complexas
4
Pólos e Zeros
Zeros
Os pólos
permitem
analisar a
estabilidade
do sistema
Pólos
O ROC está
limitada pelos
pólos!
5
Estabilidade
 Sistema causal e estável

Pólos dentro do circulo de raio unitário
 Sistema de fase mínima


Sistema estável e de inversa estável
Pólos e zeros dentro do circulo de raio unitário
6
Transformada-Z de Alguns Sinais
Sequência
Transformada
 [n]
1
a nu[n]
1
1  a.z 1
n
n.a u[n]
 a u[n 1]
n
 n.a u[n 1]
n
ROC
Pólo em ‘a’
a.z 1
za
1  a.z 
za
1
1  a.z 1
za
1 2
a.z 1
1  a.z 
1 2
Pólo duplo em ‘a’
za
 Consultar o Livro para uma tabela mais completa
7
Inversão da Transformada-Z
 Por Tabelas  (casos simples)
 Expansão em fracções parciais  (funções racionais)
N
M 1
Ak
i

a
z


k
1
k 1 1  d k .z
i 0
 Expansão em série  (polinómios)
 Resolução numérica da equação às diferenças
correspondente.
Nota: (não esquecer a ROC)
8
Propriedades da Transformada-Z
 Linearidade
 Diferenciação de X(z)
Z
a1 x1[n]  a2 x2 [n] 
a1. X 1 ( z )  a2 . X 2 ( z )
dX ( z )
n x[n]   z
dz
ROC  RX
Z
ROC contémRx1  Rx2
 Deslocação no tempo
Z
x[n  n0 ] 
z  n0 X ( z )
ROC  RX
 Multiplicação por
exponencial
Z
z0n x[n] 
X ( z / z0 )
ROC  z0 RX
 Inversão no tempo
Z
x*[n] 
X * (1 / z * )
ROC  1 / RX
 Valor inicial
x[0]  lim(1  z 1 ) X ( z ),
z 
se x[n]  0, n  0
 Conjugação
Z
x*[n] 

X * ( z* )
 Convolução no
tempo
Z
x1[n] * x2 [n] 
X1 ( z) X 2 ( z)
ROC contémRx1  Rx2
9
Resolução de Equações às
Diferenças
N
M
 a . y[n  k ]   b
k 0
k
m 0
m
.x[n  m]
Função de
sistema
TZ
N
 ak . y ( z ) z
k 0
k
M
M
  bm x( z ).z
m 0
m
y( z)
 H ( z) 

x( z )
Para o caso de condições iniciais não nulas
existe um regime transitório:
y[n]  yF [n]   a z
eq. acima
m 0
N
k
a
.
z
 k
k 0
Condições
Iniciais Nulas
N
p 0
m
b
.
z
m
k
p p
Regime transitório
(zp – pólos de H(z))
10