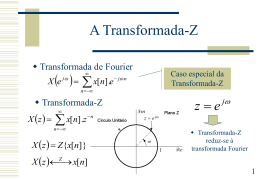
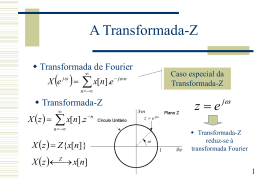
Capítulo 3. Transformada-Z
• 3.0 Introdução
• 3.1 Transformada Z – Unilateral
• 3.2 Transformada Z – Bilateral
• 3.3 Convergência
• 3.4 A Transformada-Z inversa
• 3.5 Propriedades da Transformada-Z
1
3.0 Introdução
• Regra: A Transformada Z tem a mesma regra utilizada
para sinais contínuos para Tranformada de Laplace.
• Função: É um operador linear útil para sistemas de análise
LTI e para resolver EDLCC’s.
• Tipos de Transformada-Z
– Transformada Z - Unilateral
– Transformada Z – Bilateral
– Região de Convergência (ROC)
• Tranformada Z Inversa
2
3.1.1 Transformada Z
• Definição - A tranformada Z - Uni-lateral de x(n) é dado

por
Z1 x(n)  X ( z )   x(n) z n
n  
– A variavel z é geralmente complexa e,
– A Transformada Z é uma série de potência, que pode ou não
convergir .
• Propriedades:
– Linearidade:
– Deslocamento:
•
Geralmente,
Z1ax(n)  by(n)  aX ( z)  bY ( z)

Z1x(n  1)   x(n  1) z n


 x(n) z
n 0
 n 1
 zx(0)  z[ X ( z )  x(0)]
n  
Z1 x(n  M )  z [ X ( z ) 
M
M 1
z
m  
m
x(m)]
3
3.1.2 Sequencia Exponential à direita
• Uma ferramenta básica de análise usada na transformada-Z é a
fórmula inversa da série geométrica. Se
N 1
s( N )   a(n)  a(0)  a(1)  ...  a( N  1)
n 0
onde
a (i  1)
 r  commonratio
a (i )
Então
1 rN
s( N )  a(0) r  a(0)
1 r
n 0
N 1
n

s()  a(0) r n 
e se |r|<1 (critério de convergência)
•
n 0
a(0)
1 r
Im
Usaremos freqüentemente isto em forma de somatório

1
a
(provided
 1)
1
1  az
z
n 0
onde é deduzido que
1
Z1a n u( n ) 
1  az 1
 a n z n 
a
1
Re
4
3.1.3 Sequencia Exponential à Esquerda
• Not let x(n)  anu(n  1), ( a  1)

X ( z )    a u( n  1) z
n
n  
n

1
a z
n n
n  


   a z 1   a n z n
n n
n 1
n 0
Se a 1 z  1 ou, equivalente, z  a o somatório acima converge, e
X ( z)  1 
1
1
z


1  a 1 z 1  az 1 z  a
Im
a
1
Re
5
3.1.4 Exemplo de Solução via Transformada-Z
• Problema: Assume i.c. y(0)=1. Considere o LCCDE
y(n  1)  2 y(n)  u(n).
• Solução: Aplicando a transformada-Z unilateral dos dois lados:
zY ( z)  y(0)  2Y ( z)  U ( z )

1
z

(if convergent)
– Direito = U ( z )  1z 
1
1 z
z 1
n 0
– Esquerdo = zY ( z)  y(0)  2Y ( z)  zY ( z)  1  2Y ( z)  Y ( z)(z  2)  z
n
z
z
z 1
1
– Resolvendo: Y ( z ) 



( z  1)( z  2) ( z  2) (1  z 1 )(1  2 z 1 ) 1  2 z 1
(pela expansão em frações parciais)
1 1
2
1
Y ( z) 

1
1
3
1

z
3
1

2
z
– Tranformada-Z inversa
1
2
y ( n )  u( n )  ( 2) n u( n )
3
3
6
3.2.1 Transformada-Z Bi-Lateral
• Definição - A Transformada Z Bi-Lateral de x(n) é dada por
Z 2 x(n)  X ( z ) 

 x(n) z
n
n  
Normalmente, é de interesse caracterizar steady-state
comportamento do sistema - after i.c.’s have died off. A transformada
unilateral é um caso especial da trasformada bi-lateral:
Z1x(n)  Z2 x(n)u(n)
Convergencia da Tranformada-Z Bi-Lateral (ROC)
– A região de convergencia, ou ROC de uma tranformada-Z X(z)
especifica onde X(z) é definida. Geralmente, uma ROC must be
specified as part of the Z-Transform.
– Tranformada -Z sempre converge over annular (ring-like) regions in
the complex plane: X(z) converges for
R  | z | R 


where it is possible that R  0 and/or R  .
7
3.2.2 Propriedades da Tranformada-Z Bi-Lateral
• Suponha
Z2 x(n) X ( z),
Z2 y(n) Y ( z),
Rx | z | Rx
Ry | z | Ry
and let I xy  z : Rx | z | Rx  z : Ry | z | Ry 
• Propriedades:
– Linearidade:
Z1ax(n)  by(n) aX ( z)  bY ( z), for z  I xy .
The combined ROC may expand via a pole-zero cancellation in
aX ( z )  bY ( z ) .
– Deslocamento: Z2 x(n  m) z m X ( z)  for Rx | z | Rx .
– Convolução: Se v(n)  x(n) * y (n) 
 x ( m) y ( n  m)
m  
então V ( z)  X ( z)Y ( z) for z  I xy .
The combined ROC may expand via a pole-zero cancellation in X ( z )Y ( z ) .
– Sequence Products: Se
w(n)  x(n) y(n)
1
z 1
X
(
v
)
Y
(
)v dv (Residue T heorm)

C
2j
v
para Rx Ry | z | Rx Ry .
8
Então W ( z ) 
3.2.3 Exemplo de Tranformada-Z Bi-Lateral
n
n
 1
1
x(n)     u(n)    u(n  1)
 3
2
n
Sabendo que
1
1
 1
Z
,z 
   
1
3
 3
1  z 1
3
n
1
1
1
Z
   u( n  1) 
,z 
1
2
2
1  z 1
2
Assim pelo linearidade da transformada-Z, nós temos
X ( z) 
1
1

,
1 1
1 1
1 z
1 z
3
2
1
)
12
X ( z) 
1
1
( z  )( z  )
3
2
1
1
 z, z 
3
2
Im
2 z( z 
-1/3
1/2 Re
9
3.3.1 Região de Convergência
A série de potência da tranformada-Z X(z) não converge para todas
as sequências ou valores de z.Para determinada sequência os
valores de z da tranformada converge para uma região chamada
de Região e Convergência (ROC).
Im
a
Right-sided
(causal)
Im
1
Re
a
Im
1 Re
Left-sided
(anti-causal)
a
b
Two-sided
(não-causal)
Re
10
3.3.2 Examplo de ROC
• Considere o sinal discreto
a n ; n  0
x(n)   n
b ; n  0
• Ele tem uma tranformada Bi-Lateral X ( Z ) 


1
b z
n n
n  

n

  a n z n
n 0

n
z
a

   

n 1  b 
n 0  z 
1
1

1  bz1 1  az1
provided que ambos somatório convergem. Assim a
tranformada-Z convergida requer que,
Im
z
a
 1 and
1
b
z
R
assim ROC  {z :| a || z || b |}.
Re
R
11
3.3.3 Importância da Especificação do ROC
• A importância do ROC não pode ser overemphasized. Ele é
parte da tranformada-Z.
• In specifying the Z-transform X(z) of a signal x(n), the ROC
must be given - otherwise, the Z-transform cannot be inverted
- in order to re-obtain x(n) from X(z), the ROC must be given.
• Examplo - Considere duas sequências
 0; n  0
 a n ; n  0
y (n)   n
x(n)  
n0
a ; n  0
 0;
então X ( z ) 
1
for | z || a |
1
1  az
Y ( z) 
1
for | z || a |
1
1  az
É importante entender que X(z)Y(z). The ROC’s of these
two transforms do not even intersect. Not equal!
• X(z) + ROC  unique x(n).
12
3.3.4 Diferentes tipos de sequência ROC
• Duração Finita(Finite length): x(n)  0 para n  n0 e n  n1
então ROC  {z : 0 | z | } , para z  0 e/ou z  .
• Righted-sided: x(n)  0 para n  n0
então ROC  {z : R | z | }.
• Left-sided: x(n)  0 para n  n1
então ROC  {z : 0 | z | R }.
• Two-sided (infinito):
então ROC  {z : R | z | R}.
13
3.3.5 Outras Propriedades do ROC
• ROC Shape is either Ring or disk in the plano-z centered
at the origin.
• A tranformada de Fourier converge absolutamente se
apenas se o ROC da transformada-Z de x(n) está
incluindo no círculo unitário.
• ROC não pode conter polos.
• ROC Region must be a connected region.
14
3.3.6 Estabilidade e Causalidade
• Função de Transferência : Se H(z) é a transforma- Z de
um sistema linear com resposta ao impulso unitário h(n),
i.e.,
Z2 h(n)  H ( z).
• Teorema: Um sistema linerar com função de
transferência racional Z2 h(n)  H ( z) é BIBO estável
se e apenas todos os polos de H(z) lie inside (not on) do
Im
círculo unitário.


ROC


pmax

1
Re
Círculo unitário
15
3.3.6 Observação (cont’d)
• Supondo que
K
Ak
H ( z)  
(rationalH has PFE)
1
k 1 1  pk z
K
K
entãoh(n)   Ak ( pk ) u (n)   hk (n) (WLOGpólossimples)
n
k 1
k 1
• Claramente, a transformada-Z de hk (n ) converge se
pk
apenas se
1
z
então, H(z) converge para todo z tal que
z  pmax  max pk .
1 k  K
• Facts: A ROC of causal H(z) includes the unit circle if
16
and only if all the poles of H(z) lie inside the unit circle.
3.3.6 Prova : Sufficiency (cont’d)
• Suficiência: Assumindo pk  1 para k  1,...,K. Então
K
h(n)   Ak ( pk )n u(n)
k 1
então
K
h(n)   Ak pk
e também
n
k 1


K
 h(n)  Ak pk
n 0
n 0 k 1
K

n
  Ak  pk  
k 1
n
n 0
então pk  1. Consequentemenre H(z) é a função de
transferência do sistema BIBO estável.
17
3.3.6 Prova : Necessidade (cont’d)
• Necessidade: (pela contradição) Supondo que existe um
polo pi tal que | pi |>1. Claramente, de “fato” o círculo
unitário the unit circle is not in the ROC of H(z).
– Então, existe z0 com |z0|=1 tal que H(z0) não converge
absolutamente.

H ( z0 )   h(n)( z0 ) n  
n 0
since if there is no such z0 then the unit circle is in the ROC!
– But then

 h(n)(z )
n 0
0
n


  | h(n) || z0 |   h(n)  
n
n 0
n 0
so H(z) não é BIBO estável.
QED

H ( z0 ) ||z0 |1   h(n)
n 0
18
3.3.7 Comentário sobre ROC
• Nós dizemos que o sistema g(n) é anti-causal se h(n)=g(-n)
é causal.
• Corollary: Um sistema linear anti-causal com função de
tranferência racional é BIBO estável se apenas se todos os
polos de G(z) lie outside (not on) the unit circle.
G( z)  Z2{g (n)}
• Teorema (most general): A linear system with rational
transfer function is BIBO stable if and only if the ROC
contains the unit circle.
– this applies to causal, anti-causal, or otherwise.
19
3.4.1 Transformada-Z Inversa
• Transformada-Z Inversa
X(z) + ROC  unique x(n).
• Metódos
– Inversion by Residue Theorem
– Inversion by Partial Fraction Expansion
• First-order poles
• mth-order poles
20
3.4.2 Inversion by Residue Theorem
• General Z-transform inversion formula:
1
n 1
x(n) 
X
(
z
)
z
dz

2j C
which is a contour integral in the complex plane.
• This result, which uses complex integration theory, is
made possible by Cauchy’s Residue Theorem.
• Although this formula gives the inverse Z-transform, we
will utilize much more simple table lookup procedures,
assuming rational Z-transform.
• For more information, consult the textbook.
21
3.4.3 Inversion by Partial Fraction Expansion
• A Z-transform is said to be rational if it is a ratio of rational
polynomials in z.
• If X(z) is rational, then it can be inverted
via partial fraction
1
A( z )
expansion (PFE). Assume X ( z)  B( z 1 ) , where the numerator is
of lower order than the denominator (else apply long division).
– First-order poles: X(z) has K distinct poles p1,..., pk . Then
K
Ak
1
1
k 0 z  pk
X ( z)  
where Ak  ( z 1  pk1 ) X ( z ) |z  pk .
– mth-order poles: Suppose X(z) has a (additional) pole of order m
at z  pi . Then the formula becomes
K
m
Ak
Cl
X ( z )   1


1
1
1 l
k 0 z  pk
l 0 ( z  pi )
with the Ak as above and
1
d ml 1
Cl 
( z  pi1 )m X ( z ) |z  pi
m l
(m  l )! dz
22
3.4.4 Example-1: Inverse Z-Transform
1
(1  az1 )(1  bz1 )
a 1b1

( z 1  a 1 )( z 1  b1 )
a
1
b
1
 (
)

(
)
a  b (1  az1 ) b  a (1  bz1 )
X ( z) 
The inverse Z-transform is related to the ROC of X(z). If we
assume that |a|>|b|, then

z  a  b


ROC   a  z  b

a  b  z


a
b
)a n u ( n )  (
)b n u ( n )
(right - sided)
ab
ba
b
a
x(n)  (
)b n u ( n )  (
)a n u( n  1)
(double - sided)
ba
ab
a
b
x ( n )  (
)a n u( n  1)  (
)b n u(  n  1) (left - sided)
ab
ba
x(n)  (
23
3.4.5 Example-2: Inverse Z-Transform
Consider an LTI system with input x[n] and output y[n] that satisfies the
difference equation y[n ]  5 y[n  1]  y[n ]  x[n ]  x[n  1]
2
Determine all possible values for the system’s impulse response h[n] at n=0.
5 1 2
z  z )  X ( z )(1  z 1 )
2
Y ( z)
(1  z 1 )
(1  z 1 )
2/3
1/ 3
H ( z) 




X ( z ) (1  5 z 1  z 2 ) (1  2 z 1 )(1  1 z 1 ) (1  2 z 1 ) (1  1 z 1 )
2
2
2
Y ( z )(1 
2 n
1 1 n

z

1
/
2
h
(
n
)


2
u
[

n

1
]

( ) u[ n  1]  h[0]  0

3
3 2

2 n
1 1 n
1
1
/
2

z

2
h
(
n
)


2
u
[

n

1
]

(
)
u
[
n
]

h
[
0
]



3
3 2
3
ROC  
2
1 1
 z 2
h( n )  2n u[n ]  ( ) n u[n ]
 h[0]  1
3
3
2

2
1 1
2

No
h( n )  2n u[n ]  ( ) n u[ n  1]
 h[0] 

3
3 2
324

3.5 Properties of Z-Transform
Properties
1. Linearidade:
Sequence
Z-Transform
x[n], x1[n], x2 [n]
X ( z ), X1 ( z ), X 2 ( z )
ROC
Rx , Rx1 , Rx2
ax1[n]  bx2 [n]
aX1 ( z)  bX2 ( z)
containsRx1  Rx2
z  n0 X ( z )
Rx (*)
z0n x[n]
X ( z / z0 )
z0 Rx
4. Diferenciação:
nx[n ]
z
dX ( z )
dz
Rx (*)
5. Conjugation:
x * [n ]
X * ( z*)
Re{x[n]}
[ X ( z )  X * ( z*)]/ 2
containsRx
Im{x[n]}
[ X ( z )  X * ( z*)]/ 2 j
containsRx
6. Time Reversal:
x * [ n ]
X * (1 / z*)
1 / Rx
7. Convolução:
x1[n] * x2 [n]
X1 ( z) X 2 ( z)
containsRx1  Rx2
2. Deslocamento no Tempo: x[n  n0 ]
3. Multiplicação:
8. Teorema do Valor Inicial: x[n ]  0, n  0
lim X ( z )  x[0]
z 
Rx
25