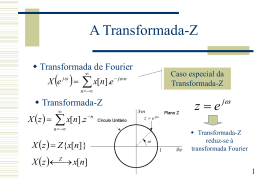
TE-072 Processamento Digital de Sinais I
-
UFPR
3. Transformada Z
3.1. Definição
Seja um sistema discreto LTI:
x[n]
Com:
h[n]
y[n]
x[n]  z n , z  Complexos
A saída y[n] pode ser calculada como:
1
TE-072 Processamento Digital de Sinais I
-
UFPR
y[n]  x[n] * h[n]
y[n] 

 h[k ]  x[n  k ]
k  
y[n] 

 h[k ]  z
nk
k  
y[n]  z n

k
h
[
k
]

z

k  
2
y[n]  z

n
 h[k ]  z
TE-072 Processamento Digital de Sinais I
-
UFPR
k
k  
Definindo:
H ( z) 

k
h
[
k
].
z

k  
Temos que:
y[n]  H ( z)  z n
Cte complexa
Logo: zn é autofunção do sistema Discreto LTI
e H(z) seu autovalor correspondente.
3
TE-072 Processamento Digital de Sinais I
-
UFPR
Logo, definimos Transformada Z do sinal
discreto x[n] como:
X ( z )  Z{x[n]} 

n
x
[
n
].
z

n  
x[n] 
 X ( z)
Z
Transformada Z Unilateral:

X ( z )   x[n].z n
n 0
Equivalente à TZ bilateral quando x[n]=0 n<0 ;
Usada p/ analisar EDCC com condições iniciais não nulas.
4
TE-072 Processamento Digital de Sinais I
-
UFPR
Escrevendo o número complexo z na sua forma polar:
z  r.e
Temos:

j
  x[n].r

X r.e j 
n
.e  jn
n  
Logo:
Se r=1:

 
X r.e j  F x[n].r n

 
X e j  Fx[n]
Transformada de Fourier
5
TE-072 Processamento Digital de Sinais I
-
UFPR
Logo: Transformada Z pode ser obtida a partir da
Transformada de Fourier fazendo:
z  e j
X ( z)  Fx[n]e j  z
O inverso nem sempre é verdade!!!
Pois:

Z x[n]  F x[n].r n

Pode fazer com que alguns sinais
se tornem convergentes
6
TE-072 Processamento Digital de Sinais I
-
UFPR
Analogia Contínuo  Discreto
Contínuo: Transformada de Laplace:

 st
x
(
t
).
e
dt

X ( s) 
s    j

Fazendo: s  j
Obtemos a Transformada de Fourier:
X ( ) 

 x(t ).e
 jt
j
dt
s

Se eixo j  ROC

X ( s) 
 x(t ).e .e

t
0
 jt

dt
Eixo j
7
TE-072 Processamento Digital de Sinais I
-
UFPR
Discreto: Transformada Z:
X ( z) 


x[n].z  n
z  r.e j
n 
ze
Fazendo:
j
Obtemos a Transformada de Fourier:
X () 

 x[n].e
 jn
Im{z}
z
n  
-1
Se circulounitário  ROC
X ( z )    x[n]r  n  .e jn
n 
r0
1
Re{z}
Circulo Unitário
8
TE-072 Processamento Digital de Sinais I
Ex.:
-
UFPR
x[n]  a u[n]
n
X ( z) 

n
n
a
u
[
n
].
z

n  

X ( z )   a .z
n
n
n 0
PG: =a.z-1 a0=1 n=


  a.z

1 n
n 0
1 n
S n  a0
1
1  (a.z 1 ) 
X ( z )  1
1  a.z 1
Converge se:
a. z  1  1
za
9
TE-072 Processamento Digital de Sinais I
Neste caso:
-
UFPR
1 0
X ( z) 
1  a.z 1
z
X ( z) 
, z a
za
Im{z}
z
-1
1
a
Re{z}
Se |a|<1  T.Fourier
|a|>1  T.Fourier
10
Ex.2:
x[n]  a u[n 1]
TE-072 Processamento Digital de Sinais I
n
X ( z) 
-
UFPR

n
n

a
u
[

n

1
].
z

n  
1
X ( z )    a .z
n
n
n  


PG:
n 1
=a-1.z

   a.z
n  
X ( z )   a .z
1
1


1 n


  a.z

1  n
n 1
n
a0= a-1.z n=
1 n
S n  a0
1
1

1

(
a
.
z
)
1
X ( z )  a z 
1  a 1.z
Converge se:
1
a .z  1
za
11
TE-072 Processamento Digital de Sinais I
Neste caso:
-
UFPR
1 0
X ( z )  a z
1  a 1.z
z
X ( z) 
, za
za
1
Im{z}
z
-1
1
a
Re{z}
Se |a|>1  T.Fourier
|a|<1  T.Fourier
12
TE-072 Processamento Digital de Sinais I
-
UFPR
Conclusão:
Sinais diferentes podem ter a mesma
expressão algébrica de X(z).
Logo uma Transformada Z
só é completamente definida se especificarmos:
- Expressão algébrica de X(z)
- Região de Convergência(ROC)
13
TE-072 Processamento Digital de Sinais I
-
UFPR
Qualquer sinal que pode ser representado como um
somatório de exponenciais complexas, poderá ser
representado por uma Transformada Z composta
de uma razão de dois polinômios.
N ( z ) aN z N  aN 1 z N 1  aN 2 z N 2  ...  a1 z1  a0 z 0
X ( z) 

D( z ) bM z M  bM 1 z M 1  bM 2 z M 2  ...  b1 z1  b0 z 0
Raízes de N(z)  Zeros da X(z)
Raízes de D(z)  Pólos da X(z)
Nos exemplos:
Valores que fazem X(z)
igual a ZERO
Valores que fazem X(z)
igual a INFINITO
z
X ( z) 
za
Zero: z=0
Pólo: z=a
14
TE-072 Processamento Digital de Sinais I
-
UFPR
Diagrama de pólos e zeros:
Representação gráfica no plano z dos pólos e zeros.
Im{z}
z
-1
1
a
Re{z}
z
X ( z) 
, z a
za
15
TE-072 Processamento Digital de Sinais I
n
Ex.3:
-
UFPR
n
1
 1
x[n]    u[n]     u[n]
 2
 3
n
 1  n
  n
1


X ( z )     u[n]     u[n] z

 3
n   
 2 
n
n
 
1
1
  
   n
X ( z )          z
n 0 
 2   3  


n

n
1
 1
X ( z )     z n      z n
3
n 0  2 
n 0 

n

1 
 1 
X ( z )    z 1      z 1 
 n 0  3 
n 0  2
n
16
TE-072 Processamento Digital de Sinais I
X ( z) 
1
1  12 z
1
1
z 
2

1
1  13 z 1
-
UFPR
z
z


z  12 z  13
1
z 
3
2 z 2  16 z
2 zz  121 
X ( z) 
 2 1
1
1
z  2 z  3  z  6 z  16
17
TE-072 Processamento Digital de Sinais I
z
z  12
z
z  13
1
z 
2
Im{z}
-1
1/2
1
-1
Re{z}
z
1
-1/3
Im{z}
2 z z  121 
X ( z) 
z  12 z  13 
-1/3
Re{z}
z
1/12
-1
UFPR
1
z 
3
Im{z}
z
-
1/2
1
Re{z}
1
z 
2
18
TE-072 Processamento Digital de Sinais I
n
-
UFPR
n
Ex.4: x[n]    1  u[n]   1  u[n  1]
 3
2
Usando os resultados das análises anteriores e a
Propriedade de Linearidade da Transformada Z.
n
z
 1
Z
   u[n] 
z  13
 3
n
z
1
Z
   u[n  1] 
z  12
2
Logo:
X ( z) 
z
z

z  13 z  12
1
z
3
1
z
2
ROC :
1
1
 z
3
2
19
TE-072 Processamento Digital de Sinais I
2 z z  121 
z
z
X ( z) 


1
1
z  3 z  2 z  13 z  12 
Im{z}
1
1
ROC :  z 
3
2
-1
UFPR
z
1
1/12
-1/3
-
1/2
Re{z}
20
TE-072 Processamento Digital de Sinais I
Ex.5:
-
UFPR
n

a
, 0  n  N 1
n
x[n]  a u[n]  u[n  N ]  
0 , outros
X ( z) 

N 1
n  
n 0
n
n n
x
[
n
].
z

a

 .z
N 1

X ( z )   a.z
n 0
PG: a0=1 =a.z-1 n=N


1 n
1 n
S n  a0
1

1 N
1  a.z
X ( z )  1
1  a.z 1
X(z) converge se
Isto é:
a.z 
1 N

a  e z 0
21


TE-072 Processamento Digital de Sinais I
-
UFPR
1 N
1  a.z
1  a N .z  N
X ( z )  1

1
1  a.z
1  a.z 1
zN  aN
N
N
N
1
z

a
X ( z)  z
 N 1 
za
z
za
z
Pólos da X(z):
Zeros da X(z):
z N 1  0  N  1 pólos em z  0
z  a  0  pólo em z  a
z N  a N  0  Zeros raízes do polinôm io
zeros em z  a.e j 2k / N  k  0,1, ..., N  1
Quando k=0: zero em z=a logo cancela com o pólo em z=a
22
TE-072 Processamento Digital de Sinais I
-
UFPR
Logo tem-se: N-1 pólos em z=0
N-1 zeros distribuídos uniformemente sobre
um círculo de raio a
p/ N=8
Im{z}
-1
(7)
z
2k/8
1
a
Re{z}
ROC: Todo plano z com exceção de z=0
23
TE-072 Processamento Digital de Sinais I
-
UFPR
3.2. Propriedades da ROC
Considerando X(z) uma função racional em z e
x[n] finito p/n finito
1) A ROC de X(z) é um anel ou disco centrado na origem (z=0)
2) A Transformada de Fourier de x[n] converge absolutamente
se e somente se a ROC de X(z) inclui
a circunferência unitária.
3) A ROC não contém pólos de X(z)
4) Se x[n] tem duração finita, x[n]0 p/ -<N1nN2<,
a ROC é todo plano z com possíveis exceções em z=0 e z=
24
TE-072 Processamento Digital de Sinais I
-
UFPR
5) Se x[n] é definida à direita, x[n]=0 p/ n<N1<,
a ROC estende-se de |z|=r0 (maior pólo) até , incluindo ou não z=
6) Se x[n] é definida à esquerda, x[n]=0 p/ n>N2>,
a ROC será |z|<r0 (menor pólo), incluindo ou não z=0
7) Se x[n] é definida à esquerda e à direita,
a ROC será um anel compreendido entre 2 pólos.
8) A ROC deve ser uma região conexa.
25
TE-072 Processamento Digital de Sinais I
-
UFPR
3.3. Transformada Z Inversa
Demonstração da fórmula de inversão.

X ( z )  F x[n].r  n


  F x[n].r 
x[n].r  F X r.e 
1
x[n]  r 
X r.e .e

2
X r.e
j
n
n
1
j
j
n
jn
.d
2
1
x[n] 
2
 X r.e . re  .d
j
j n
2
26
TE-072 Processamento Digital de Sinais I
1
x[n] 
2
-
UFPR
 X r.e . re  .d
j
j n
2
z  r.e j
Mudança de variáveis:
dz  jr.e j .d
1 1
d   j  dz
j r.e
Variando  de 0 a 2  z varia sobre uma circunferência
de raio r. |z|=r  ROC de X(z)
x[n] 
x[n] 
1
2 j

r
zn
X ( z )   dz
z
1

2 j
X ( z )  z n1  dz
r
Resolve-se utilizando o Teorema dos Resíduos
27
TE-072 Processamento Digital de Sinais I
Pares de Transformadas Z
x[n]
X (z )
 [n]
1
Todo Plano Z
z
z 1
z
z 1
z 1
u[n]
 u[n  1]
 [n  n0 ]
n
a u[n]
 a u[n 1]
n
z
 n0
z
za
z
za
-
UFPR
ROC
z 1
Todo Plano Z exceto:
z  0 p / n0  0
z   p / n0  0
za
za
28
TE-072 Processamento Digital de Sinais I
X (z )
x[n]
n
n.a u[n]
2
n
n .a u[n]
n 1.a u[n]
n
a.z
z  a 2
a.z.z  a 
3
z  a 
z2
z  a 2
-
UFPR
ROC
za
za
za
cos0 n.u[n]
zz  cos0 
z 2  2 cos 0 .z  1
z 1
sin0n.u[n]
z sin 0 
z 2  2 cos 0 .z  1
z 1
29
TE-072 Processamento Digital de Sinais I
x[n]
X (z )
r cos0n.u[n]
z r
r sin0n.u[n]
z.r. sin 0 
z 2  2r cos0 .z  r 2
z r
n
a , 0  n  N  1

0 , outros
n
zN  aN
N 1
z z  a 
UFPR
ROC
zz  r. cos0 
z 2  2r cos0 .z  r 2
n
-
z 0
30
TE-072 Processamento Digital de Sinais I
-
UFPR
3.3.1. Inversão por Inspeção
Consiste no uso eficiente das tabelas e propriedades
da Transformada Z
31
TE-072 Processamento Digital de Sinais I
-
UFPR
3.3.2. Expansão em Frações Parciais
Revisão:
Dado G(v) função racional em v com grau N(v) < grau D(v)
N (v )
G (v ) 
D (v )
r
Pode ser escrita na forma
i
Aik
G (v)  
k
i 1 k 1 v  pi 
Onde:
r = número de pólos
i = multiplicidade do pólo i
Aik = coeficiente relativo a k-ésima parcela do pólo i
32
TE-072 Processamento Digital de Sinais I
-
UFPR
Onde:


 i k


1
d
i
Aik 
  i k v  pi  .G(v) 
 i  k !  dv
 v  pi
Ex.:
s2  4
H ( s) 
( s  2) 2 ( s 2  2s  2)
Pólos: duplos em s=-2 e complexo s=-1j
1=2
2=1 3=1
r=4
33
TE-072 Processamento Digital de Sinais I
s2  4
A
B
Cs  D
H ( s) 


 2
2
2
2
(s  2) (s  2s  2) (s  2)
s  2 s  2s  1

-
UFPR


1  d 2 2
2
A
 22 s  2 H ( s) 
2  2!  ds
 s 2
s2  4
8
A 2
 4
s  2s  2 s 2 2



1  d 21
2
B
 21 s  2  H ( s ) 
2  1!  ds
 s  2
d  s2  4 
2s 2  4s  8

B   2
 4
2
3
2
ds  s  2 s  2  s  2 s  4 s  8s  8s  4 s  2
34
TE-072 Processamento Digital de Sinais I
Pólo complexo:
No caso:
-
UFPR
Cs  D
A'
B'


s 2  2s  2 s  R  jI s  R  jI
Cs  D  ( A' B' )s  A' ( R  jI )  B' ( R  jI )

1  d 11
A' 
 11 ( s  1  j ) H ( s )
(1  1)!  ds
 s  1 j
s2  4
42j
A' 

 1  0.5 j
2
( s  2) ( s  1  j ) s  1 j
4

1  d 11
B' 
 11 ( s  1  j ) H ( s )
(1  1)!  ds
 s  1 j
s2  4
42j
B' 

 1  0 .5 j
2
( s  2) ( s  1  j ) s  1 j
4
35
TE-072 Processamento Digital de Sinais I
-
UFPR
P/ funções com coeficientes reais: sempre B’=A’*
Logo:
Assim:
C  2. Re{A'}
D  2Re{ p}. Re{A'}  Im{p}. Im{A'}
C  2.(1)  2
D  2(1)(1)  (0.5)(1)  3
s2  4
4
2
 2s  3
H ( s) 


 2
2
2
2
(s  2) (s  2s  2) (s  2)
s  2 s  2s  1
Matlab: função residue
[r,p,k]=residue(n,d)
36
TE-072 Processamento Digital de Sinais I
-
UFPR
No caso específico da Transformada Z
Como as funções básicas são na forma:
z
za
A expansão em frações parciais não pode ser aplicada
diretamente na X(z).
Soluções:
1) Aplicar o método na função:
2) Aplicar o método na função:
X ( z)
z
 
X z
1
Matlab: função residuez
[r,p,k]=residuez(n,d)
37
3z  z
Ex.: X ( z ) 
z  14 z  13 
2
Método 1:
TE-072 Processamento Digital de Sinais I
5
6
-
UFPR
3z  56
X ( z)

z  14 z  13 
z
X ( z)
A
B


1
z
z  4 z  13
3z  56
1


A

z


1
4
z  14 z  13 
1
z
4
3z  56
1

 2
B

z

3
1
1
z  4 z  3 
1
z
3
38
TE-072 Processamento Digital de Sinais I
Logo:
-
UFPR
X ( z)
1
2


1
z
z  4 z  13
z
2z
X ( z) 

1
z  4 z  13
Por tabela temos:
x[n]  
 u[n]  2  u[n]
1 n
4
1 n
3
39
TE-072 Processamento Digital de Sinais I
-
UFPR
3z 2  56 z
X ( z) 
z  14 z  13 
Método 2:
5 1
3

A
B
1
6 z
X (z ) 

 1 1
1 1
1 1
1 1
1 4 z 1 3 z
1 4 z
1 3 z



3  56 z 1
1 1
A

1

4 z
1 1
1 1
1 4 z 1 3 z

3  56 z 1
1 1
B

1

3 z
1 1
1 1
1 4 z 1 3 z









1
z  14
2
z  13
40
TE-072 Processamento Digital de Sinais I
1
1
X (z ) 
1 z
1
4
1

-
UFPR
2
1 z
1
3
1
Por tabela temos:
x[n]  
 u[n]  2  u[n]
1 n
4
1 n
3
41
TE-072 Processamento Digital de Sinais I
-
UFPR
3.3.2. Expansão em Série de Potência
Definição da Transformada Z  Série de Laurent
X ( z) 

n
x
[
n
].
z

n  
X ( z)  ... x[2].z 2  x[1].z  x[0]  x[1].z 1  x[2].z 2  ...
42
TE-072 Processamento Digital de Sinais I
Ex.:
-
UFPR
z
X ( z) 
z  0.5
x[n]  (0.5)n u[n]
Sabemos por tabela:
n
0
1
2
3
4 ...
Isto é:
x[n] 1  0.5 0.25  0.125 0.0625....
Podemos calcular a série de potência de uma razão
de polinômios por divisões sucessivas:
43
TE-072 Processamento Digital de Sinais I
-
UFPR
z  0.5
z
1  0.5 z 1  0.25z  2  0.125z 3  ....
 z  0.5
 0.5
0.5  0.25z 1
0.25z 1
 0.25z 1  0.125z  2
 0.125z  2
0.125z  2  0.0625z 3
....
44
Ex.2:



X ( z)  z 2 1  12 z 1 1  z 1 1  z 1

TE-072 Processamento Digital de Sinais I
-
UFPR
Pólos somente em z=0, frações parciais não é apropriado.
Multiplicando todos os termos:
X ( z)  z  z 1  z
2
1
2
1
2
1
De tabela temos:
x[n]   [n  2]  12  [n  1]   [n]  12  [n 1]
Ex.3:


X ( z)  log 1 az1 , z  a
45
TE-072 Processamento Digital de Sinais I
3.4.Propriedades da Transformada Z
-
UFPR
46
TE-072 Processamento Digital de Sinais I
-
UFPR
Exercícios:
1)
z2
X ( z) 
,
z  14 z  12 
2)
z  2z 1
X ( z)  2 3
z  2 z  12
z  12
2
3)
z3  2z 2  z
X ( z)  2 3
z  2 z  12
Verificar as respostas usando Divisões Sucessivas
47