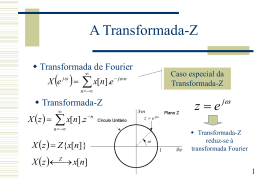
Transformada Z
Processamento Digital de Sinais
IFBA/GPSC
1
Transformada de Fourier
1
x[n] 
2
X ( ) 

j n
X
(

)
e
d



 j n
x
[
n
]
e

n  
IFBA/GPSC
2
Transformada Fourier

Vantagem:


Análise direta do espectro (componentes
de freqüência) do sinal discreto;
Desvantagens:


A manipulação algébrica não é prática;
Existem muitos sinais discretos cuja
transformada de Fourier não existe.
IFBA/GPSC
3
Transformada Z
X ( z) 

n
j
x
[
n
]
z
,
no
qual
z

re

n  
X ( z) r 1  X ()
A transformada de Fourier é um caso
específico da transformada Z.
IFBA/GPSC
4
Transformada Z
Critério de convergência da Transformada de Fourier :


 x[n]  
n  
Critério de convergência da Transformada Z:


 x[n]r
n
A convergência depende,
também, dos valores de r,
ou seja do |z|.

n  
IFBA/GPSC
5
Região de Convergência


Qual o intervalo de valores de r que garante
a convergência da Transformada Z?
Ex.:
x[n]  u[n]
X ( z) 

 u[n]z
n
n  
IFBA/GPSC
6
Região de Convergência

 u[n]z
n

n  
ROC
Im

 n  jwn
r
 e 
n 0

Re
n
1
  

n 0  r 
Circunferência
Unitária
ROC : r  1
IFBA/GPSC
Representação Polar
7
Representação Útil
Num( z ) ( z  zer1 )(z  zer2 )...(z  zerM )
X ( z) 

Den( z )
( z  p1 )(z  p2 )...(z  pN )


zer= zeros de X(z), ou seja, as raízes do
polinômio no numerador ( Num(z) ).
p= pólos de X(z), ou seja, as raízes do
polinômio no denominador ( Den(z) ).
IFBA/GPSC
8
Região de Convergência (ROC):
Propriedades



A região de convergência é um disco ou um
anel centrado na origem;
A região de convergência não contém pólos;
Se a região de convergência contém a
circunferência unitária (r=1) existe a
transformada de Fourier.
IFBA/GPSC
9
Seqüência de Tempo Positivo
O sinal é nulo para n < 0.
Ex.:

x[n]
...
n
A região de convergência (ROC) é composta pela
área externa ao maior pólo de valor absoluto finito.
IFBA/GPSC
10
Exemplo
x[n]
Im
...
n
x
1
x[ n]  u[ n]
z
X ( z) 
z 1
Re
Circunferência
Unitária
ROC : r  1
IFBA/GPSC
11
Seqüência de Tempo Negativo
O sinal é nulo para n > 0.
Ex.:

x[n]
...
n
A região de convergência (ROC) é composta pela
área interna ao menor pólo de valor absoluto
finito.
IFBA/GPSC
12
Exemplo:
x[n]  (2 n  3n )u[n]
5z
2
6
X ( z) 
(1  z / 2)(1  z / 3)
Im
Re
x x
2 3
ROC : r  2


Pólos: z=2 e z=3
Zeros: z=12/5
IFBA/GPSC
13
Seqüência Bilateral

x[n] não é de tempo positivo ou
negativo.
...
...
n
ROC : p1  r  p2
P1 maior pólo que contribui para n > 0
P2 menor pólo que contribui para n < 0
IFBA/GPSC
14
Exemplo:
Im
n
n
 1
1
x[n]     u[n]    u[n  1]
 3
2
1

2z  z  
 12 
X ( z) 
1 
1

z

z




3 
2

x oo x
-1/3
1/2
Re
1/12
ROC : 1/ 3  r  1/ 2
IFBA/GPSC
15
Seqüência de Duração Finita

Têm duração limitada de n=N1 até
n=N2.
N1

N2
n
A ROC contém todo plano z, exceto
possivelmente em z=0 e/ou z=
IFBA/GPSC
16
Exemplos


Ex.:
x[n]=[n], ROC contém todos os
valores de z, incluindo z=0 e z=.
x[n]=[n-1], ROC contém todos os
valores de z, excluindo z=0.
IFBA/GPSC
17
Estabilidade

O sistema h[n] é estável se

 h[n]  
n  

Então:
Um sistema é estável se a ROC contém a
circunferência unitária.
Um sistema Causal é Estável se todos os pólos estão
dentro círculo unitário
IFBA/GPSC
18