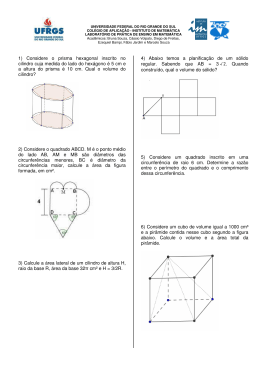
ESPCEX – MATEMÁTICA 2
01 - Um sistema de irrigação é formado por seis canais que se
cruzam como na figura. As dimensões das seções transversais
dos canais são apresentadas a seguir.
Calcule o volume de água armazenado no sistema.
02 - Observe as figuras a seguir.
Calcule as medidas da altura e da aresta da base dessa pirâmide.
04 - Em um tanque no formato de um cubo de aresta 25 cm,
contendo líquido, foi posta uma pirâmide P (fig.1), de altura igual a 6 cm, com a base apoiada no fundo do tanque. Com isso, o nível de líquido passou de 18 cm para 19 cm.
a) Calcule o volume, em cm¤, da pirâmide P .
b) A pirâmide P foi retirada do tanque e o nível de líquido voltou ao inicial. Uma pirâmide P‚ (fig.2), de 30 cm de altura, foi
então posta no tanque, com a base apoiada no fundo, o que elevou em 2 cm o nível de líquido.
Determine o volume da pirâmide P‚.
A figura I mostra a forma do toldo de uma barrada, e a figura
II, sua respectiva planificação, composta por dois trapézios isósceles congruentes e dois triângulos.
Calcule:
a) a distância h da aresta åæ ao plano CDEF;
b) o volume do sólido de vértices A, B, C, D, E e F, mostrado na
figura I, em função de h.
03 - João recorta um círculo de papel com 10 cm de raio. Em
seguida, dobra esse recorte ao meio várias vezes, conforme ilustrado na figura 1.
Depois de fazer diversas dobras, abre o papel e coloca o
número 1 nas duas extremidades da primeira dobra. Sucessivamente, no meio de cada um dos arcos formados pelas dobras anteriores, João escreve a soma dos números que estão
nas extremidades de cada arco.
A figura 2 a seguir ilustra as quatro etapas iniciais desse
processo.
Considere que João recortou a dobradura referente à figura
da etapa 3 na linha que corresponde à corda AB indicada na figura 3.
Ele verificou, ao abrir o papel sem o pedaço recortado, que
havia formado o polígono da figura 4.
Considere o polígono formado por João, do qual são retirados dois triângulos isósceles (figura 5).
Com os triângulos restantes é possível formar a superfície
lateral de uma pirâmide hexagonal regular (figura 6).
PROFESSOR: TÚLIO
05 - Quatro dos oito vértices de um cubo de aresta unitária são
vértices de um tetraedro regular. As arestas do tetraedro são
diagonais das faces do cubo, conforme mostra a figura.
a) Obtenha a altura do tetraedro e verifique que ela é igual a
dois terços da diagonal do cubo.
1
ESPCEX – MATEMÁTICA 2
b) Obtenha a razão entre o volume do cubo e o volume do tetraedro.
06 - Dentro de uma lata de óleo, no formato de um cilindro circular reto, com capacidade de 900 ml e altura de 20 cm, colocase um paralelepípedo reto, de base quadrada, de forma que esta base esteja totalmente apoiada no fundo da lata e que seus
vértices toquem as laterais da lata. Determine a altura desse
paralelepípedo, sabendo que seu volume é de 10% do volume
total da lata.
07 - Um cilindro circular reto é inscrito em um cone, de modo
que os eixos desses dois sólidos sejam colineares, conforme
representado na ilustração a seguir.
A altura do cone e o diâmetro da sua base medem, cada
um, 12 cm.
Admita que as medidas, em centímetros, da altura e do raio
do cilindro variem no intervalo ]0;12[ de modo que ele permaneça inscrito nesse cone.
Calcule a medida que a altura do cilindro deve ter para que
sua área lateral seja máxima.
08 - Uma empresa de engenharia fabrica blocos na forma de
um prisma, cuja base é um octógono regular de lado 20 cm e
altura 1 m. Para fabricar esses blocos, a empresa utiliza um
molde na forma de um cilindro circular reto, cujo raio da base e
a altura medem 1 m, conforme a figura abaixo. Calcule o volume do material necessário para fabricar o molde para esses
blocos.
09 - A figura abaixo representa uma seringa no formato de um
cilindro circular reto, cujo êmbolo tem 20 mm de diâmetro. Esta
seringa está completamente cheia de um medicamento e é usada para injetar doses de 6 ml desse medicamento. Com base
PROFESSOR: TÚLIO
nessas informações, determine quantos milímetros o êmbolo se
desloca no interior da seringa ao ser injetada uma dose.
TEXTO PARA A PRÓXIMA QUESTÃO
As tecnologias atuais, além de tornar os equipamentos eletroeletrônicos mais leves e práticos, têm contribuído para evitar
desperdício de energia. Por exemplo, o ENIAC (Eletronic Numerical Integrator and Computer) foi o primeiro computador eletrônico digital e entrou em funcionamento em fevereiro de 1946.
Sua memória permitia guardar apenas 200 bits, possuía milhares de válvulas e pesava 30 toneladas, ocupando um galpão
imenso da Universidade da Pensilvânia - EUA. Consumia energia correspondente à de uma cidade pequena.
O ENIAC utilizava o sistema numérico decimal, o que acarretou grande complexidade ao projeto de construção do computador, problema posteriormente resolvido pelo matemático húngaro John Von Neumann, que idealizou a utilização de recursos
do sistema numérico binário, simplificando o projeto e a construção dos novos computadores.
10 - Considere o formato do ENIAC um bloco retangular de volume igual a 396 m¤. Sabendo que o ENIAC tinha 5,5 metros de
altura e 30 metros de comprimento, a medida de sua largura,
em metros, é igual a
a) 2,4.
b) 2,8.
c) 3,0.
d) 3,3.
e) 4,0.
TEXTO PARA A PRÓXIMA QUESTÃO
Uma caixa de embalagens dos Correios, em formato de paralelepípedo reto-retângulo, foi utilizada pelo partido A para envio de materiais de campanha (cartazes, santinhos, ...) nas últimas eleições.
11 -
A função S(x) que representa a área da folha de papelão retangular utilizada para construção da caixa, conforme a planificação dada na figura, é
a) S (x) = 4x£ + 900x + 48600
b) S (x) = 630 x + 48600
c) S (x) = -4x£ + 180x + 48600
2
ESPCEX – MATEMÁTICA 2
d) S (x) = -3x£ - 135x + 81000
e) S (x) = 3x£ - 135x - 81000
TEXTO PARA A PRÓXIMA QUESTÃO
Água é dom da vida e sinal de esperança. O cuidado com a
água deve ser uma preocupação não mais exclusiva dos que
vivem em regiões consideradas áridas ou semi-áridas, mas de
todos no planeta.
(Anadete Gonçalves Reis.
http://www.cliquesemiarido.org.br/mc/mc_06_10.pdf)
Cisterna é um tipo de reservatório d'água cilíndrico, coberto
e semi-enterrado, que permite a captação e o armazenamento
de águas das chuvas, aproveitadas a partir do seu escoamento
nos telhados das casas, através de calhas.
(http://www.cliquesemiarido.org.br/mc/mc_11_15.pdf)
12 -
A medida, em graus, do ângulo AFC é
a) 30°
b) 45°
c) 60°
d) 90°
15 - Um depósito com 3,6m de altura, 4,8m de largura e 7,2m
de comprimento foi planejado para armazenar caixas cúbicas,
todas de mesmo tamanho, sem que houvesse perda de espaço. Pode-se estimar que o menor número de caixas cúbicas
necessárias para encher completamente esse depósito é:
a) 24
b) 36
c) 48
d) 72
16 - Um engenheiro deseja projetar um bloco vazado cujo orifício sirva para encaixar um pilar. O bloco, por motivos estruturais, deve ter a forma de um cubo de lado igual a 80 cm e o orifício deve ter a forma de um prisma reto de base quadrada e altura igual a 80 cm, conforme as figuras seguintes. É exigido que
o volume do bloco deva ser igual ao volume do orifício.
Uma cisterna cilíndrica comporta 18.000 litros de água. Sabendo que a sua altura h é igual a 2,40 m, a medida aproximada do diâmetro da cisterna, em metros, é
a) 2,5
b) 3,2
Dado:
c) 4,8
Volume = ™r£ h
d) 5,0
Adote ™ = 3
e) 10,0
13 - O cubo de vértices ABCDEFGH, indicado na figura, tem
arestas de comprimento a.
É correto afirmar que o valor "L" do lado da base quadrada
do prisma reto corresponde a:
a) 20Ë2 cm
b) 40Ë2 cm
c) 50Ë2 cm
d) 60Ë2 cm
e) 80Ë2 cm
17 - Um copo de base quadrada está com 80% de sua capacidade com água. O maior ângulo possível que esse copo pode
ser inclinado, sem que a água se derrame é
Sabendo-se que M é o ponto médio da aresta AE, então a
distância do ponto M ao centro do quadrado ABCD é igual a
a) (aË3)/5
b) (aË3)/3
c) (aË3)/2
d) aË3
e) 2aË3
14 - Considere o cubo de aresta a representado abaixo.
PROFESSOR: TÚLIO
a) 45°
b) 30°
3
ESPCEX – MATEMÁTICA 2
c) 60°
d) 15°
e) I, II e III.
21 -
18 - A figura a seguir representa a planificação de um cubo cujas faces foram numeradas de 1 a 6.
O produto dos números que estão nas faces adjacentes à
face de número 1 é
a) 120.
b) 144.
c) 180.
d) 240.
e) 360.
19 - Considere o trapézio ABCD da figura a seguir, obtido pela
interseção de um cubo de aresta 1 com um plano que passa
por dois vértices opostos A e D de uma face e pelos pontos
médios B e C de arestas da face não adjacente.
A área do trapézio ABCD é
a) (3Ë2)/5.
b) 5/3.
c) (3Ë5)/2.
d) (Ë6)/2.
e) 9/8.
20 - A figura 1 a seguir representa um prisma reto de base hexagonal regular.
As figuras A e B indicam, respectivamente, planificações de
sólidos em forma de prisma e pirâmide, com todas as medidas
sendo dadas em metros. Denotando por V e V‚ os volumes do
prisma e da pirâmide, respectivamente, conclui-se que V representa de V‚
a) 25%.
b) 45%.
c) 50%.
d) 65%.
e) 75%.
22 - Uma pirâmide regular tem por base um hexágono cuja diagonal menor mede 3Ë3 cm. As faces laterais desta pirâmide
formam diedros de 60° com o plano da base. A área total da pirâmide, em cm£, é
a) 81(Ë3) / 2
b) 81(Ë2) / 2
c) 81/2
d) 27Ë3
e) 27Ë2
23 - Dadas três retas paralelas não situadas no mesmo plano,
toma-se sobre uma delas um comprimento AB dado e, arbitrariamente, um ponto C sobre a segunda reta e um ponto D sobre
a terceira reta.
A respeito do volume da pirâmide triangular ABCD, podemos afirmar que é diretamente proporcional a:
a) AD
b) AC
c) AB
d) BC
e) BD
24 - Considere o cubo de aresta 3 cm e vértices ABCDEFG.
Considere o ponto P situado no prolongamento da aresta EA de
modo que PA = 5 cm, como está estabelecido na figura.
Considerando as planificações I, II e III, quais delas podem
ser do prisma?
a) Apenas I.
b) Apenas II.
c) Apenas I e II.
d) Apenas II e III.
PROFESSOR: TÚLIO
4
ESPCEX – MATEMÁTICA 2
A maior e a menor aresta lateral da pirâmide PEFGH medem, respectivamente:
a) Ë82 cm e 8 cm
b) Ë82 cm e 4 cm
c) Ë43 cm e 8 cm
d) 20 cm e 10 cm
e) 12 cm e 8 cm
25 - A grande pirâmide de Quéops, antiga construção localizada no Egito, é uma pirâmide regular de base quadrada, com
137 m de altura. Cada face dessa pirâmide é um triângulo isósceles cuja altura relativa à base mede 179 m.
A área da base dessa pirâmide, em m£, é:
a) 13.272
b) 26.544
c) 39.816
d) 53.088
e) 79.432
26 - A partir de quatro dos vértices de um cubo de aresta 6,
construído com madeira maciça, foram recortadas pirâmides
triângulares congruentes, cada uma tendo três arestas de medida 3, conforme representado na figura 1.
O sólido obtido após a retirada das pirâmides está representado na figura 2, a seguir.
28 - As bases ABCD e ADGF das pirâmides ABCDE e ADGFE
são retângulos e estão em planos perpendiculares. Sabe-se
também que ABCDE é uma pirâmide regular de altura 3 cm e
apótema lateral 5 cm, e que ADE é face lateral comum às duas
pirâmides.
Se a aresta AF é 5% maior que a aresta AD, então o volume
da pirâmide ADGFE, em cm¤, é
a) 67,2.
b) 80.
c) 89,6.
d) 92,8.
e) 96.
29 - Uma artesã confecciona dois diferentes tipos de vela ornamental a partir de moldes feitos com cartões de papel retangulares de 20 cm × 10 cm (conforme ilustram as figuras abaixo). Unindo dois lados opostos do cartão, de duas maneiras, a
artesã forma cilindros e, em seguida, os preenche completamente com parafina.
O volume do sólido obtido é
a) 198.
b) 204.
c) 208.
d) 212.
e) 216.
27 - Assinale a(s) proposição(ões) correta(s).
(01) Considere L e L‚, duas latas de forma cilíndrica, de massa
de tomate, de mesma marca. A lata L possui o dobro da altura
da lata L‚, mas seu diâmetro é a metade do diâmetro de L‚. Se
L custa R$ 1,80 e L‚ R$ 2,80, então a lata mais econômica é
L‚.
(02) Observe a figura 1. Se os diâmetros dos semicírculos estão sobre os lados do triângulo retângulo ABC, então Área I =
Área II + Área III.
(04) A figura 2 está representando uma pirâmide inscrita num
cubo. Se o volume da pirâmide é de 72 m¤, então a aresta do
cubo é igual a 9 m.
(08) O octaedro regular é um poliedro que tem 8 arestas.
Supondo-se que o custo da vela seja diretamente proporcional ao volume de parafina empregado, o custo da vela do tipo I, em relação ao custo da vela do tipo II, será
a) o triplo.
b) o dobro.
c) igual.
d) a metade.
e) a terça parte.
30 - Considere o losango cujos lados medem 6 cm e um dos
ângulos internos mede 60°.
A rotação desse losango em torno de um de seus lados gera um sólido cujo volume, em centímetros cúbicos, é
a) 146 (Ë3) ™
b) 162 ™
c) 162 (Ë3) ™
d) 178 ™
e) 178 (Ë3) ™
PROFESSOR: TÚLIO
5
ESPCEX – MATEMÁTICA 2
31 - O diâmetro da base de um reservatório cilíndrico mede 2
metros. Sabendo-se que sua altura mede 60 centímetros, sua
capacidade aproximada, em litros, é de
a) 1.884
b) 1.970
c) 2.764
d) 3.140
32 - Para a obtenção do índice pluviométrico, uma das medidas
de precipitação de água da chuva, utiliza-se um instrumento
meteorológico denominado pluviômetro.
A ilustração abaixo representa um pluviômetro com área de
captação de 0,5 m£ e raio interno do cilindro de depósito de 10
cm.
Considere que cada milímetro de água da chuva depositado
no cilindro equivale a 1 L/m£.
No mês de janeiro, quando o índice pluviométrico foi de 90
mm, o nível de água no cilindro, em dm, atingiu a altura de, aproximadamente:
a) 15
b) 25
c) 35
d) 45
33 - A terra retirada na escavação de uma piscina semicircular
de 6 m de raio e 1,25 m de profundidade foi amontoada, na
forma de um cone circular reto, sobre uma superfície horizontal
plana. Admita que a geratriz do cone faça um ângulo de 60°
com a vertical e que a terra retirada tenha volume 20% maior
do que o volume da piscina.
Nessas condições, a altura do cone, em metros, é de
a) 2,0
b) 2,8
c) 3,0
d) 3,8
e) 4,0
34 - Um troféu para um campeonato de futebol tem a forma de
uma esfera de raio R = 10 cm cortada por um plano situado a
uma distância de 5Ë3 cm do centro da esfera, determinando
uma circunferência de raio r cm, e sobreposta a um cilindro circular reto de 20 cm de altura e raio r cm, como na figura (não
em escala).
O volume do cilindro, em cm¤, é
a) 100 ™
b) 200 ™
c) 250 ™
d) 500 ™
e) 750 ™
35 - A figura indica algumas das dimensões de um bloco de
concreto formado a partir de um cilindro circular oblíquo, com
uma base no solo, e de um semicilindro.
Dado que o raio da circunferência da base do cilindro oblíquo mede 10 cm, o volume do bloco de concreto, em cm¤, é
a) 11.000 ™.
b) 10.000 ™.
c) 5.500 ™.
d) 5.000 ™.
e) 1.100 ™.
GABARITO
1. 834 m¤
2. a) h = 0,8 m
b) V = 8h
3. Ø = Ë(200 - 100Ë2) cm
h = 10 Ë(Ë2 - 1) cm
4. a) 625 cm¤
b) (16875/13) cm¤.
5. a) (2Ë3)/3
Observe a figura
b) 3
6. ™ cm
PROFESSOR: TÚLIO
6
ESPCEX – MATEMÁTICA 2
7. 6 cm
8. (™ - 0,1928) m¤
9. 60/™ mm
10. [A]
11. [A]
12. [B]
13. [C]
14. [C]
15. [D]
16. [B]
17. [A]
18. [C]
19. [E]
20. [D]
21. [E]
22. [A]
23. [C]
24. [A]
25. [D]
26. [A]
27. 01 + 02 = 03
28. [C]
29. [B]
30. [B]
31. [A]
32. [A]
33. [C]
34. [D]
35. [A]
PROFESSOR: TÚLIO
7