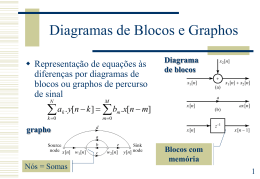
Diagramas de Blocos e Graphos
 Representação de equações às
diferenças por diagramas de
blocos ou graphos de percurso
de sinal
N
M
 a . y[n  k ]   b
k 0
k
m 0
m
Diagrama
de blocos
.x[n  m]
grapho
Blocos com
memória
Nós = Somas
1
Implementação Directa Tipo I e II
Implementação
directa tipo I
N
(grafos)
M
 a . y[n  k ]   b .x[n  m]
k 0
Implementação
directa tipo II
k
m 0
m
a0  1
2
Forma em Cascata
 Secções de segunda ordem
Em geral é sempre possível expressar um dado filtro
decomposto em pólos e zeros.
N
M1
H ( z)  A
 (1  f
k 1
M1
k
M2
z ) (1  g k z 1 )(1  g k* z 1 )
1
k 1
M2
1
1
* 1
(
1

c
z
)
(
1

d
z
)(
1

d
 k  k
kz )
k 1
k 1
b0k  b1k z 1  b2k z 2
H ( z)  A
1
2
k 1 1  a1k z  a2 k z
Pólos complexos
conjugados
Pólos reais
3
Forma Paralela
Np
N1
Ak

1
1

c
z
k 0
k
H ( z )   Ck z  
1
k 0
Bk (1  ek z 1 )

1
* 1
k 0 (1  d k z )(1  d k z )
N1
e0 k  e1k z 1
H ( z )   Ck z  
1
2
k 0
k 0 1  a1k z  a2 k z
Np
1
N1
4
Formas Transpostas
 Se trocarmos a entrada com a saída e invertermos as
direcções de todos os ramos de um grapho linear, a
função de transferência não se altera.
H1(z)
H1(z)
H2(z)
H2(z)
Daqui resultam as
formas transpostas
5
Filtros FIR
 Realização directa e transposta de filtros FIR
M
y[n]   bm .x[n  m]
m 0
6
Filtros FIR de Fase Linear
(Generalizada)
Resposta em
frequência:
j
j
H (e )  A(e ) e
 j (    )
=0  Fase
estritamente linear
Atraso de grupo constante  ( )   d {arg[ H (e j )]}  
d
(não há distorção de fase):
Tipo I
Tipo II
Tipo III
Tipo IV
0nM
h[n]  h[M  n], M par
h[n]  h[M  n], M impar
h[n]  h[M  n], M par
h[n]  h[M  n], M impar
d     M / 2
d – atraso de
grupo
(em amostras)
7
Problemas Numéricos
 quantização (arredondamentos ou truncagens ....)

Nos coeficientes do filtro
Pode tornar o sistema estável
 Modifica a resposta do sistema


Nos sinas

Produz ruído
Diferentes estruturas têm diferentes
comportamentos numéricos
8
Problemas Numéricos
Filtro Elíptico passa banda de ordem 12
Implementação em
cascata
Estrutura
directa
9
Ciclos Limite
 Devido aos erros de quantização pode existir
saída sem existir entrada!
Solução:
arredondar em
direcção a zero.
Mas tal aumenta os
erros de
arredondamento!
yˆ [ n]  Q[a yˆ[n  1]]  x[n]
Resposta Impulsiva para a=-1/2 e
palavras de três bits
Outro
exemplo
a=-3/4
10