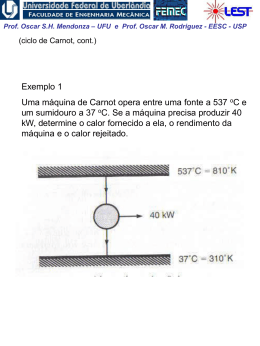
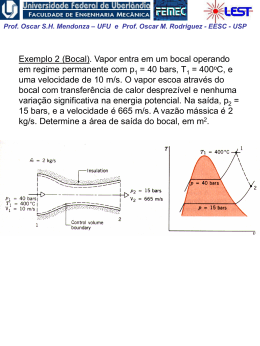
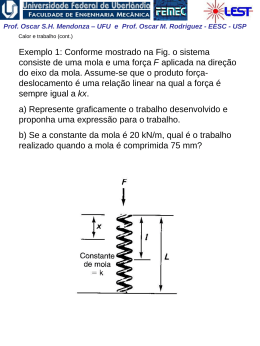
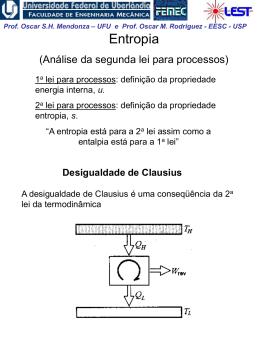
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
1ª Lei da Termodinâmica para sistemas (cont.)
A Propriedade Termodinâmica Entalpia
H = U + PV visto que todas essas quantidades são
ENTALPIA
h = u + pv
propriedades termodinâmicas, funções
apenas dos estado do sistema, sua
combinação também deve possuir
essas mesmas características
Exemplo: calor é transferido para um sistema em um processo
quase-estático a pressão constante, (ΔEC = ΔEP = 0).
W
1
Q2  U 2  U1 1W2
Neste caso a pressão é constante,o
sistema de massa2 fixa:
1
W2 
1
 pdV  p  dV  pV
2
1
 V1 
1
Portanto:
1
Q2  U 2  U1  p2V2  p1V1  U 2  p2V2   U1  p1V1 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Conclusão: o calor transferido em um processo quaseestático a pressão constante é igual à variação da
entalpia do processo!
1
Q2  H 2  H1
Obs: resultado válido apenas para este caso restrito.
Para processos que ocorrem com variação de
pressão, entalpia não tem esse significado físico;
porém, sendo uma propriedade termodinâmica,
entalpia é uma função de ponto, ou seja, não
depende do processo. Sendo assim, é válida
para qualquer processo a seguinte relação:
u  h  pv
O estado de referencia, nas tabelas de vapor de
agua, é o do líquido saturado a 0,01 oC, onde a
energia interna recebe o valor zero. Assim, é
possível termos valores negativos de entalpia.
Na região de saturação:
h  hl  xhlv
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Calores Específicos a Volume e a Pressão
Constantes
CALOR ESPECÍFICO: a quantidade de calor
necessária para elevar a temperatura de uma
unidade de massa da substância em 1 grau.
calor
1 Q
c

massa  T m T
(Considera-se apenas
uma fase homogênea,
sólida, líquida ou gasosa)
Para uma substância simples compressível e processo
quase estático ( ΔEC = ΔEP = 0 e  W = pdV ), da 1a lei
da termodinâmica:
Q  dU  W  dU  pdV
1. Volume constante (pdV = 0):
cv 
1  Q 
1  U   u 




  
m  T v m  T v  T v
2. Pressão constante (  dU  pdV   U 2  U1  pV2  pV1  H 2  H1  dH):
1  Q 
1  H   h 
cp     
  
m  T  p m  T  p  T  p
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Obs: calores específicos também são propriedades
termodinâmicas!
Para sólidos e líquidos:
dh  du  d  pv   du

(praticamente
incompressíveis)
0
Assim:
dh  du  c dT
cv ou c p
Obs.: para temperaturas não muito baixas e para um
intervalo não muito grande de temperaturas:
cv  c p  c  constante
Assim, para sólidos e líquidos:
h2  h1  u2  u1  cT2  T1 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
EXEMPLO 1: Vapor inicialmente úmido, contendo 3%
de umidade a 7,5 kPa, é condensado até a saturação
do líquido. Quanto calor foi retirado por Kg de vapor,
assumindo o processo a pressão constante?
EXEMPLO 2: Calor é fornecido a pressão constante
para uma máquina turboélice como mostrado na Fig.
Se a temperatura do ar é aumentada de 20oC para
500oC na câmara de combustão, determine o calor
transferido por kg de ar. A pressão na câmara de
combustão é de 1 MPa e supomos um calor específico
constante cp = 1,0062 kJ / (Kg K) para o ar durante o
processo.