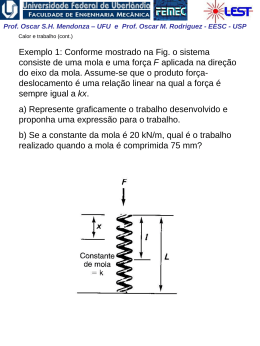
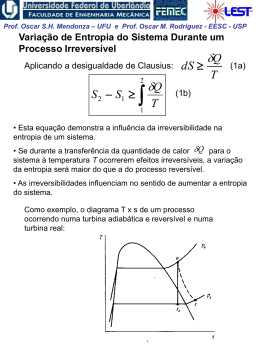
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Calor e Trabalho
Definição de trabalho mecânico: “produto escalar de
uma força aplicada sobre um corpo ou sistema pelo
deslocamento”
2
W   F  dx
1
requerida a relação funcional
entre força e trabalho
Definição termodinâmica de trabalho: “Trabalho é
realizado por um sistema se o único efeito sobre os
arredores possibilitar o levantamento de um peso”
Definição do sinal do trabalho:
• (+) W é o trabalho feito pelo sistema (sistema
perde energia)
• (-) W é o trabalho feito sobre o sistema (sistema
ganha energia)
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Suponha um sistema composto por fluido cujos
limites são adiabáticos (sistema isolado).
Em (b), a polia gira pela ação da queda de um peso
e, como consequência, ocorre o aquecimento do
fluido no sistema isolado (aumenta a temperatura).
Houve transferência de calor?
Em (a), substituindo-se o sistema isolado por outra polia,
fica claro que o único efeito externo da iteração dos dois
sistemas seria levantar o peso; trata-se, portanto, de
trabalho.
Qualquer processo que envolve só iterações de trabalho
é definido como processo adiabático.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Trabalho Abiabático: Energia Potencial
O trabalho necessário para mudar a posição de um
corpo num caqmpo gravitacional:
F  m.g  mg
 
wad  mg  dz
ad = adiabático
Integrando:
Wad  m.g.(Z2  Z1 )  Ep
Eenergia potencial gravitacional  Ep  Wad
Temos então a energia potencial gravitacional, a qual é
independente do processo realizado.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Trabalho adiabático: Energia Cinética
O trabalho necessário para mudar a quantidade de
movimento de um corpo,num campo de velocidades:



dv
F  ma  m
dt
 
ds  v dt
 dv 
 Wad   m  .  vdt   mv .dv
 dt 
Integrando:
m 2
2
Wad    v2  v1   c
2
Temos então a energia cinética, a qual é independente
do processo realizado.
Wad  dU  d  m kT 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Trabalho adiabático: Energia interna
O trabalho necessário para mudar a energia sensível
de um corpo:
A integração de forças de natureza microscópica (forças
de fusão nuclear, forças eletrostáticas, forças de atração
mássica, forças de inércia ) relacionadas a um Campo de
Temperaturas na forma de energias associadas é
chamada de energia interna (u)
Supondo que a energia interna é apenas função da
temperatura (normalmente um fato com gases ideais):
Wad  dU  d m  kT 
Integrando:
Wad  U  mk T2  T1 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Portanto:
 Limite adiabático exclui qualquer iteração que
não seja trabalho (isola o sistema).
 A lei de Newton combinada com o conceito de
processo adiabático, permite obter as formas
mecânicas da energia.
energia total (E) de um sistema, será a somatória dos
trabalhos adiabáticos realizados ou recebidos pelo
sistema
Etotal = E interna + E cinética + Epotencial + Eeletrostática + Emagnética
+ ....
O conceito de trabalho freqüentemente está relacionado a
formas específicas de uma quantidade chamada energia.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Interações entre Trabalho e Calor
Trabalho realizado pela fronteira móvel de um sistema
simples compressível em um processo quase-estático
(composto por estados termodinâmicos de equilíbrio)
O processo quase estático é um processo ideal e pode
ser imaginado se retirarmos gradativamente pesos de
massa infinitesimalmente pequena do pistão
W  pAdL
ou
W  pdV
É necessário conhecer a relação entre pressão e volume!
Conceito importante: Trabalho só pode ser identificado
nas fronteiras do sistema.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Considerando como sistema o gás, contido num cilindro
com êmbolo, sofrendo um processo de expansão quaseestático:
2
2
W2   W 
1
1
 pdV
1
(-) Trabalho realizado sobre o sistema
(+) Trabalho realizado pelo sistema
Podemos visualizar o trabalho realizado como a área
debaixo do processo
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Verificamos através do gráfico acima que trabalho é
função do caminho. Assim, trabalho é uma função de
linha. Em outras palavras, W é uma diferencial
inexata.
Propriedades termodinâmicas são funções de ponto,
ou diferenciais exatas.
Elas não dependem do caminho, ou seja
2
 dV  V
2
 V1
: é usado para diferenciais inexatas (como trabalho)
1
d:
é usado para diferenciais exatas (como volume)
Para trabalho, escrevemos:
2
 W
1
 1W2
W2  W1
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Há duas classes de problemas para a determinação de
2
W2 
1
 pdV
1
1. Soluções gráficas, e
2. Relações funcionais entre p e V. Neste caso, um
exemplo é o processo politrópico, onde:
P  V n  cte
Esta solução não é
válida para n = 1.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Trabalho em processos quase - estáticos
realizados por gás ideal
Processo isotérmico (T = cte):valido para
gases ideais ou qualquer gas com coeficiente
de compressibilidade diferente da unidade
pV  cte.
p1V1  p2V2  cte.
p1v1  p2v2  cte.
w12  
2
1
2 dv
cte
dv  cte 
1 v
v
w12  p1v1 ln(v2 / v1 )
 RT1
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Processo isobárico (Pressão = cte.):valido
para gas ideal ou qualquer gas ou fluido
compressivel
RT1 RT2
p1  p2 

 cte
v1
v2
pv0  cte.
w12   ctedv  p1  v2  v1  .
2
1
Qualquer processo realizado por um gás seja ideal
ou não, pode ser representado por uma equação
simples num diagrama p-v, isto é:
pvn  cte.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Portanto:
• Processo isotérmico(qualquer gás ):
• Processo isobárico(qualquer gás):
• Processo isocórico(qualquer gás):
pv = cte; n = 1
pv° = cte; n = 0
pvºº = cte; n = 8
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Problema ilustrativo
Para o processo pv = cte, uma compressão de gás é
desenvolvida de uma pressão inicial de 200 kPa
até uma final de 800 kPa. Se o volume específico
inicial é 0,1 m3/Kg,
(a) determine o trabalho por quilo de gás;
(b) Avalie este problema graficamente (área sob a
curva pressão-volume)
processo a pv=cte
Dados:
p1=200 "kpa"
p2=800"kpa"
v1=0,1"m^3/kg"
Equações:
p1*v1=p2*v2
W=p1*v1*ln(v2/v1)
Resposta:
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
0
800
750
-5
700
650
-10
550
W12
p2
600
-15
500
450
-20
400
350
-25
300
250
-30
200
0,02
0,03
0,04
0,05
0,06
v2
0,07
0,08
0,09
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP