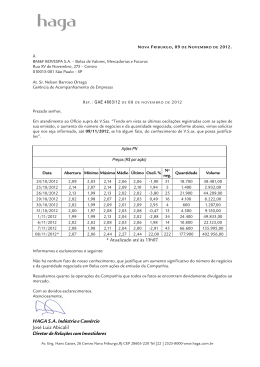
DISCIPLINA INTEGRADORA II
TEOREMAS DE HAGA E
A DIVISÃO DE UM SEGMENTO
EM n PARTES IGUAIS
A ÁRVORE DAS DOBRADURAS E
A ÁRVORE BINÁRIA
Você pode dividir o lado do quadrado de
papel em 2 partes iguais?
Sim, é fácil!
E em 4?
Também é fácil!
Agora divida em 3 ...
É difícil?
É possível dividir em 3, ou mesmo em um
número inteiro qualquer, somente dobrando.
Vamos ver agora...
Divisão em 3 partes (trisecção) 
1º Teorema de Haga:
Dado o quadrado unitário ABCD e P o ponto
médio de AB, se T é a intersecção do lado CD
com o lado AD, após a dobra que faz
coincidir o vértice C com o ponto P, então
|DT| = 1/3.
B
P
A
B
P
A
E
T
C
D
C
D
Divisão em 3 partes (trisecção) 
2º Teorema de Haga:
Dado o quadrado unitário ABCD e P o ponto
médio de AB, se S é o ponto onde se
encontra o vértice B, após a dobra CP, e T é
o ponto onde inicia a dobra que faz coincidir
D com S, mantendo o vértice C fixo, então
|DT| = 1/3.
B
P
A
P
S
S
T
C
DC
A
P
A
D
T
C
D
Divisão em 3 partes (trisecção) 
3º Teorema de Haga:
Dado o quadrado unitário ABCD e P o ponto
médio de AB, consideremos a dobra que leva
o ponto P sobre o lado BC, ao mesmo tempo
que o vértice C é levado sobre o lado AD. Se
T é o ponto do lado AD onde o vértice C se
encontra após a dobra, então |DT| = 1/3.
B
P
A
P
A
T
C
D
E
D
Divisão em n partes 
A seguir...
Dado um segmento AP qualquer do lado AD do
quadrado unitário ABCD, vamos estabelecer dois
tipos de dobras: Paralela e Oblíqua
A
B
AD = 1
P
AP = 1/m
C
D
Paralela: é a que faz juntar o vértice A com o
ponto P, mantendo o lado AB paralelo ao lado CD
do quadrado. Obtemos assim o ponto M,
intersecção da dobra com o lado AD.
A
A
B
B
M
M
AM = 1/(2m)
P
P
C
D
C
D
Dado um segmento AP qualquer do lado AD do
quadrado unitário ABCD, vamos estabelecer dois
tipos de dobras: Paralela e Oblíqua
A
B
AD = 1
P
AP = 1/m
C
D
Oblíqua: é a que faz juntar o vértice C com o ponto
P, tornando o lado BC oblíquo em relação aos
outros. Obtemos assim o ponto N, intersecção do
lado BC com o lado AB, após a dobra.
N
A
A
B
BN
P
C
D
P
C
D
BN = 1/(2m-1)
PROPOSIÇÃO:
A partir de um segmento inicial de medida 1/m,
depois de uma dobradura paralela, ele se
reduzirá à metade de seu comprimento,
passando o segmento derivado a medir 1/(2m);
depois de uma dobradura oblíqua, o segmento
derivado passará a medir 1/(2m-1).
P
|AM| = 1/(2m)
|AP| = 1/m
O
|BN| = 1/(2m-1)
Demonstração de:
|AP| = 1/m  |BN| = 1/(2m-1)
x
N
A
B
P
C
E
y
D
Ex.: Dividir o lado do quadrado em 14 partes
iguais.
1/14
14 = 2 x 7
P
7=2x4–1
O
4=2x2
P
2=2x1
P
1/7
1/4
1/2
1
TEOREMA:
Em um número com representação
binária, associando a cada dígito 1 uma
dobradura paralela e a cada dígito 0 uma
dobradura oblíqua, a seqüência de dobraduras
que leva do lado do quadrado a 1/n dele é dada
pela seqüência dos dígitos da representação
binária do número n-1.
A Árvore das Dobraduras
1
p
1/2
O
P
1/3
1/4
O
P
1/5
O
1/9
O
1/6
P
O
1/11
1/10
O
1/k+1
1/2k+1
P
1/2k+2
P
1/7
P
1/12
O
1/13
1/8
P
O
1/14
O
1/15
1/m
1/2m-1
P
1/2m
P
1/16
A Árvore Binária
1
0
0
0
4
1
8
0
2n
9
2n-1
1
2
0
1
1
1
0
10
0
5
1
0
12
11
0
2k
6
k
1
2k+1
3
1
1
13
0
7
1
14
0
15
2n-1
1
2n+1-1
A Árvore Binária
0
1
1
0
1
2
0
1
8
0
5
4
0
1
0
1
6
1
10
9
Representação
binária de n-1
Ex.: (13)10 = (1101)2
3
0
11
7
1
12
0
13
14
1
15
A Árvore das Dobraduras
O
1/3
O
P
1
P
1/2
P
O
1/4
P
Seqüência de
dobraduras para
obter 1/n
Ex.: 1/14 => P P O P
1/5
1/6
1/7
1/8
O
P
O P
O P
O
P
1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16
Referências:
Revista do Professor de Matemática: nº 16 e nº 50
http://www.origami.gr.jp