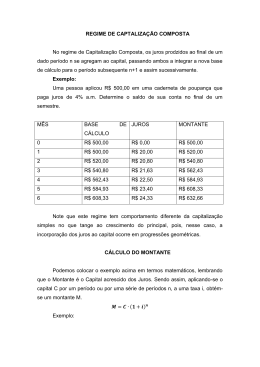
Matemática Financeira
Renato Tognere Ferron
FLUXO DE CAIXA
CONCEITOS
Fluxo de caixa de um projeto ou investimento é o
conjunto de entradas e saídas de capital ao longo
do tempo.
(+)
(-)
Entradas
Saídas
tempo
Saídas
Entradas
(-)
tempo
(+)
Representação em diagrama
3
Diagrama de Fluxo de Caixa
Fluxos convencionais de investimentos
+
-
Diagrama de Fluxo de Caixa
Fluxos convencionais de empréstimo
+
-
EXEMPLOS
Como será representado no diagrama de fluxo
de caixa um investimento no valor de R$
100.000,00 pelo qual o investidor recebeu R$
150.000,00 após 6 meses?
6
EXEMPLOS
Como será representado no diagrama de fluxo
de caixa um empréstimo tomado de R$
50.000,00 pelo qual o tomador pagará R$
75.000,00, após 5 meses?
7
EXEMPLOS
Desenhe o diagrama de fluxo de caixa de uma
série de depósitos de R$ 10.000,00 cada um,
feitos no início de cada mês durante um ano
numa Caderneta de Poupança que rendeu, no
fim do ano, um montante final de R$
200.000,00.
8
EXEMPLOS
Desenhe o diagrama de fluxo de caixa para
uma pessoa que, durante 6 meses, fez
depósitos de R$ 25.000,00 numa Caderneta de
Poupança, sempre no início de cada mês. Nos
três meses que se seguiram, perdeu o emprego
e foi obrigada a fazer retiradas de R$
60.000,00, também no início de cada mês,
tendo esgotado o seu saldo.
9
REGIMES DE CAPITALIZAÇÃO DOS JUROS
SIMPLES: os juros de cada período são calculados
SEMPRE sobre o valor inicial;
COMPOSTA: os juros de cada período são
calculados sobre o valor inicial e também sobre os
juros acumulados até o início de cada período.
JUROS SIMPLES
CONCEITO
Ao emprestarmos uma quantia em dinheiro, por
determinado período de tempo, costumamos
cobrar o juro, de tal modo que, no fim do prazo
estipulado, disponhamos não só da quantia
emprestada, como também de um acréscimo que
compense a não-utilização do capital financeiro, por
nossa parte, durante o período em que foi
emprestado.
CONCEITO
A soma capital + juros é chamada de montante e
será representada letra M
Montante (M) = Capital (C) + Juros
C = Capital disponível
i = Taxa de juros
C
0
i
J1
M11
J1 = Remuneração por
dispor do Capital C
durante o período 1
JUROS
Os juros são fixados através de uma taxa percentual
que sempre se refere a uma unidade de tempo: mês,
bimestre, trimestre, semestre, ano,... .
Utilizamos, usualmente, a letra i para denotar a
taxa de juros. A letra i é a inicial da palavra inglesa
interest, que significa juros.
REPRESENTAÇÃO
O elemento que faz a equivalência dos valores ao
longo do tempo é o juro, que representa a
remuneração do capital.
Exemplo:
I = 24% ao ano = 24% a.a
I = 6% ao trimestre = 6% a.t
I = 3,5% ao mês = 3,5% a.m
EXEMPLO
Imagine que o Banco X cobra uma taxa de 6% ao
mês no uso do cheque especial. E em determinado
mês, João precisou pegar emprestado do banco R$
2.000,00. Que valor João deve depositar na sua
Conta daqui a um mês para saldar a dívida?
EXEMPLO
Juros = Capital x taxa x nº de período = C x i x n
6% x 2000 = (6/100) x 2000 x 1 = 0,06 x 2.000 = 120
Resposta = 2.000 + 120 = 2.120
REPRESENTAÇÃO
É importante observar que no cálculo anterior, a taxa
de juros 6% foi transformada em fração decimal para
permitir a operação. Assim, as taxas de juros terão
duas representações:
i) Sob a forma de porcentagem (taxa percentual):
6% ao ano = 6% a.a.
ii) Sob a forma de fração decimal: 6 / 100 = 0,06.
J= C x i x n
Exemplo 1:
Uma pessoa aplica $ 18.000,00 à taxa de 1,5% ao
mês. Determine o valor dos juros acumulados e o
valor de resgate ao final do período.
Sol:
C = $ 18.000,00
i = 1,5% = 0,015 ao mês
J = Cxi = 18.000,00x 0,015 = 270
M1 = C + J1 = 18000 + 270 =
R$ 18.270,00
Exemplo 2:
Calcular os juros simples produzidos pelo capital de
R$ 200,00 em 3 meses, à taxa de 5% ao mês.
Sol:
C = R$ 200
t = 3 meses
i = 5% a. m. = 0,05 ao mês
j = ? = C*i*n = 200 * 0,05 * 3 = R$ 30,00
Exemplo 3:
Consideremos que um capital de R$ 500,00 fique
depositado durante 25 dias em uma aplicação que
paga 1,1% ao dia. Qual o valor dos juros simples?
Sol:
C = R$ 500
t = 25 dias
i = 1,1% ao dia = 0,011 ao dia
j = ? = C*i*t = 500 * 0,011 * 25 =
R$ 137,50
EXERCÍCIOS
(Cesgranrio – Petrobras – Técnico em Administração e Controle Júnior –
2009) – Hugo emprestou certa quantia a Inácio a juros simples, com taxa
mensal de 6%. Inácio quitou sua dívida em um único pagamento feito 4
meses depois. Se os juros pagos por Inácio foram de R$ 156,00, a quantia
emprestada por Hugo foi
a) menor do que R$ 500,00.
b) maior do que R$ 500,00 e menor do que R$ 1.000,00.
c) maior do que R$ 1.000,00 e menor do que R$ 2.000,00.
d) maior do que R$ 2.000,00 e menor do que R$ 2.500,00.
e) maior do que R$ 2.500,00.
EXERCÍCIOS
(Cesgranrio – Petrobras Distribuidora – Técnico em Administração – 2010) –
Um capital C, submetido ao regime de juros simples durante 5 meses,
propicia um rendimento correspondente à metade de C. A taxa mensal de
juros utilizada é de
a) 2%
b) 5%
c) 10%
d) 20%
e) 50%
CÁLCULO DO MONTANTE
C = Capital disponível
i = Taxa de juros
C
0
Que valor deveríamos ter
no final do 1º período ?
i
J1
M11
J1 = Remuneração por
dispor do Capital C
durante o período 1
M1 = C + J1
M1 = C + (i x C)
M1 = C x (1 + i)
C
0
M1
J1
1
M2
J2
2
Capitalização simples
M 2 = C + J1 + J2
M2 = C + (i x C) + (i x C)
M2 = C x (1 + i x 2)
Que valor deveríamos ter
no final do período 2 ?
C
0
M1
J1
1
J2
M2
M3
2
3
J3
Capitalização simples
M3 = C + J1 + J2 + J3
M3 = C + (i x C) + (i x C) + (i x C)
M3 = C x (1 + i x 3)
Que valor deveríamos ter
no final do período 3 ?
C
0
M1
J1
1
M2
2
J2
M3
J3
3
Mn
n-1
Mn = C + J1 + J2 + J3 + ... + Jn
Capitalização simples
Mn = C (1 + i n)
x
x
Que valor deveríamos ter
no final do período n ?
Jn
n
EQUAÇÕES BÁSICAS
Regime de JUROS SIMPLES
jn = C x i x n
Mn = C x (1 + i x n)
IMPORTANTE
As variáveis i e n devem estar
na mesma unidade de tempo
Exemplos:
Prazo em meses
Prazo em anos
Prazo em dias
Taxa em % ao mês
Taxa em % ao ano
Taxa em % ao dia
1) Calcular os juros simples e o montante de
um capital de R$ 1.000,00 aplicado à taxa
de 2% a.m., durante 6 meses;
2) Calcular os juros simples produzidos por
um capital de R$ 2.000,00 aplicado à taxa
de 1% a.m. durante 1 ano e 2 meses;
3) Um capital de R$ 4.000,00 rendeu em um
mês a importância de R$ 1.000,00 de
juros. Calcule a taxa de juros simples.
4) Calcular o capital que, aplicado à taxa de
1% a.m., produz em 13 meses juros
simples de R$ 650,00.
5) Calcular o montante de um capital de R$
1.200,00 empregado à taxa de juros
simples de 0,5% a.m. durante 2 anos e 6
meses.
EXERCÍCIOS
EXERCÍCIOS
Um capital de R$ 2.400,00 será aplicado à taxa de 5% ao mês, durante 2
meses, sob regime de juros simples. O valor final obtido, em reais, será
a) 2.520,00
b) 2.640,00
c) 2.646,00
d) 2.650,00
e) 2.652,00
EXERCÍCIOS
O investimento, que proporcionou a um investidor obter um montante de R$
15.000,00 aplicado a uma taxa de juros simples de 1,5% ao mês, pelo período
de seis meses, em reais, foi
a) 12.222,22
b) 13.718,13
c) 13.761,46
d) 14.061,75
e) 14.138,93
EXERCÍCIOS
Um investidor aplicou a importância de R$ 2.000,00, gerando uma
remuneração de R$ 400,00 ao final de um período de 1 ano. De acordo com o
regime de juros simples com capitalização anual, a taxa anual de juros dessa
operação foi
(A) 5%
(B) 10%
(C) 12%
(D) 20%
(E) 25%
EXERCÍCIOS
O Banco WS emprestou a um de seus clientes a quantia de R$ 12.000,00, a
uma taxa de 5% ao mês, no regime de juros simples, para pagamento único
no final de 90 dias. De acordo com as condições do empréstimo, o cliente
deverá pagar ao Banco, em reais, o montante total de
(A) 12.600,00
(B) 12.800,00
(C) 13.200,00
(D) 13.600,00
(E) 13.800,00
FIM
Obrigado pela atenção!
Renato Tognere Ferron
[email protected]
3331-8661
39