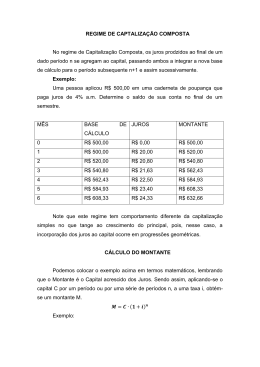
MATEMÁTICA PARA NEGÓCIOS
MATEMÁTICA PARA NEGÓCIOS
PROF. VICENTE EUDES
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Plano de Ensino
Aula 1:
Matemática Básica
Aula 2:
Função do 1º Grau e Aplicação de métodos
quantitativos à Administração
Aula 3:
Função do 2º Grau e Aplicação de métodos
quantitativos à Administração
Aula 4:
Matemática Financeira – Capitalização
Simples e Capitalização Composta
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Matemática Financeira – Capitalização
Simples e Capitalização Composta
- Juros Simples
- Capital
- Montante
- Taxa de juros
- Juros compostos
- Taxas Equivalentes
AULA 4
MATEMÁTICA PARA NEGÓCIOS
1 - JUROS E CAPITALIZAÇÃO SIMPLES
1.1 – JUROS
JURO é a remuneração do capital emprestado, podendo ser
entendido, de forma simplificada, como sendo o aluguel pago pelo
uso do dinheiro.
1.2 - CAPITAL
Capital é qualquer valor expresso em moeda e disponível em
determinada época.
1.3 - TAXA DE JUROS
Taxa de juros é a razão entre os juros recebidos (ou pagos) no fim
de um período de tempo e o capital inicialmente empregado. A taxa
está sempre relacionada com uma unidade de tempo (dia, mês,
trimestre, semestre, ano etc.)
AULA 4
MATEMÁTICA PARA NEGÓCIOS
1.4 - CAPITALIZAÇÃO SIMPLES
Capitalização simples é aquela em que a taxa de juros
incide somente sobre o capital inicial, não incide, pois,
sobre os juros acumulados. a taxa varia linearmente em
função do tempo. Se quisermos converter a taxa diária em
mensal, basta multiplicar a taxa diária por 30; se
desejarmos uma taxa anual e tendo a mensal, basta
multiplicar por 12, e assim por diante.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
CÁLCULO DOS JUROS
Valor dos juros é obtido da expressão:
J=Cxixn
onde:
j = valor dos juros
C = valor do capital inicial ou principal
i = taxa
n = prazo (tempo)
M = Montante final (M = C + J)
AULA 4
MATEMÁTICA PARA NEGÓCIOS
EXEMPLOS
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Qual o valor dos juros correspondentes a um empréstimo
de R$ 10.000,00, pelo prazo de 15 meses, sabendo-se que a
taxa cobrada é de 3% a m. ?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Um capital de R$ 25.000,00, aplicado durante 10 meses,
rende juros de R$ 5.000,00. Determinar a taxa
correspondente?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Uma aplicação de R$ 50.000,00 pelo prazo de 180 dias
obteve um rendimento de R$ 8.250,00. Indaga-se: Qual a
taxa anual correspondente a essa aplicação?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Sabendo-se que os juros de R$ 12.000,00 foram obtidos,
com as aplicação de R$ 15.000,00, à taxa de juros de 8%
ao trimestre, pede-se que calcule o prazo?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Qual o capital que, à taxa de 2,5% ao mês, rende juros de
R$ 18.000,00 em 3 anos?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Em que prazo uma aplicação de R$ 35.000,00 pode gerar
um montante de R$ 53.375,00, considerando-se uma taxa
de 30% ao ano?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Você fez um empréstimo de R$5.000,00 a uma taxa de juro
simples de 12% ao ano a ser pago em dois anos. O valor a
ser pago é próximo de:
a) R$6.200,00
b) R$6.270,00
c) R$4.030,00
d) R$4.070,00
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Qual o valor presente de uma aplicação em juros
simples de cinco anos, taxa de juro de 14% ao ano e
valor de resgate, único, igual a R$100.000,00?
a) R$58.823,00
b) R$51.936,00
c) R$52.854,00
d) R$59.325,00
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Uma empresa toma empréstimo de R$150.000,00 à taxa
de 1,8% ao mês no regime de capitalização simples.
Sabendo que a amortização será feita seis meses após a
contratação do empréstimo, calcule o montante a ser
pago no final deste período.
a) R$166.946,73
b) R$312.000,00
c) R$151.620,00
d) R$166.200,00
AULA 4
MATEMÁTICA PARA NEGÓCIOS
EXEMPLO 10: Um investidor faz empréstimo de R$140.000,00 à taxa
de 1,95% ao mês no regime de capitalização simples. Sabendo que
a amortização será feita cinco meses após a contratação do
empréstimo, qual o valor a ser pago no final deste período?
a) R$153.650,00
b) R$140.546,00
c) R$152.635,00
d) R$126.350,00
AULA 4
MATEMÁTICA PARA NEGÓCIOS
2 - JUROS COMPOSTOS
2.1 - CAPITALIZAÇÃO COMPOSTA.
Quando uma determinada soma de dinheiro está aplicada a juros
simples, os juros são sempre calculados sempre sobre o
montante inicial. quando uma soma está aplicada a juros
compostos, os juros são calculados não apenas sobre o
capital inicial, mas sobre este capital acrescido dos juros já
vencidos.
Capitalização composta é aquela em que a taxa de juros incide
sobre o principal acrescido dos juros acumulados até o período
anterior. Neste regime de capitalização a taxa varia
exponencialmente em função do tempo.
O conceito de montante é o mesmo definido para capitalização
simples, ou seja, é a soma do capital aplicado ou devido mais o
valor dos juros correspondentes ao prazo da aplicação ou da
divida.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
M = C ( 1 + i)n
1. Calcular o montante de um capital de R$ 1.000,00,
aplicado à taxa de 4% ao mês, durante 5 meses.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
M = C ( 1 + i)n
2. Calcular o montante de um capital de R$ 2.000,00,
aplicado à taxa de 4% ao mês, durante 1 ano.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
M = C ( 1 + i)n
3. Qual o montante de uma aplicação de R$ 15.000,00,
pelo prazo de 9 meses, à taxa de 2% ao mês.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
M = C ( 1 + i)n
4. No final de 6 meses, o Sr João deverá efetuar um pagamento de
R$ 200.000,00 referente ao valor de um empréstimo contraído hoje,
mais os juros devidos, correspondente a uma taxa de 4% ao mês.
Qual o valor emprestado?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
M = C ( 1 + i)n
5. Qual o capital que, aplicado durante 1 ano a uma
taxa de 4% ao mês produz o montante de R$ 3000,00?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
3 - Taxas Equivalentes
Já sabemos que duas taxas são equivalentes quando
aplicadas a um mesmo capital, durante o mesmo período de
tempo, produzem o mesmo rendimento.
Na capitalização simples, duas taxas proporcionais são
também equivalentes. Na capitalização composta, não.
No regime de juros compostos, uma aplicação que paga 10%
a.m. representa o rendimento, em um trimestre, de:
Atribuindo um capital R$ 100, temos:
M = 100(1,1)3  M = 10  1,331  M = R$ 133,10.
Portanto o rendimento no trimestre foi de 33,1%.
Logo, 10% ao mês é equivalente a 33,1% ao trimestre.
Ambas podem ser utilizadas nos problemas; são efetivas.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Taxas Equivalentes
Podemos generalizar o cálculo da equivalência entre
taxas assim:
Equivalência entre ANO e MÊS: 1 + ia = (1 + im)12
Equivalência entre ANO e TRIMESTRE: 1 + ia = (1 + it)4
Equivalência entre SEMESTRE e MÊS: 1 + is = (1 + im)6
Observamos que o lado da igualdade que contém a
menor das unidades de tempo envolvidas, fica elevado
ao expoente igual a quantas vezes a menor unidade
“cabe” na maior.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
EXEMPLOS
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Calcular o montante gerado a partir de R$ 1.500,00, quando
aplicado à taxa de 60% ao ano com capitalização mensal,
durante 1 ano.
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Aplicando R$ 800,00 à taxa de juros de 12% ao ano, com
capitalização bimestral, durante um ano e meio, qual o valor
do montante?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Qual a taxa anual equivalente a 3% ao mês?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Qual a taxa anual equivalente a 30% ao semestre com
capitalização bimestral?
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Qual é a taxa equivalente ao semestre de uma taxa de
12% ao ano?
a) 6,14% ao semestre
b) 5,83% ao semestre
c) 5,39% ao semestre
d) 6,26% ao semestre
AULA 4
MATEMÁTICA PARA NEGÓCIOS
Um investidor tem duas alternativas para investir R$ por
um mesmo prazo: (i) a uma taxa de 10% ao semestre e
(ii) a uma taxa de 21% ao ano. Neste caso:
a) As duas alternativas são idênticas, pois as taxas são
equivalentes
b) A melhor alternativa é a alternativa (i)
c) A melhor alternativa é a alternativa (ii)
d) A melhor alternativa é a (ii) para prazos iguais ou
menores a um ano
AULA 4