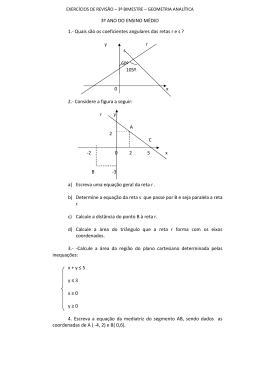
Questão 1
Calcule a área do trapézio em destaque na
figura, assumindo que os valores numéricos
no plano cartesiano estão em centímetros.
Resposta
Resposta
Como a reta passa pelos pontos (0; 1) e (1; 3), o
3 −1
seu coeficiente angular é a =
= 2 . Logo a
1 −0
reta é o gráfico da função do primeiro grau
f(x) = 2x + 1 para x ≥ 0.
A região destacada é um trapézio de bases
f(2) = 2 ⋅ 2 + 1 = 5 cm e f(4) = 2 ⋅ 4 + 1 = 9 cm, e
altura 4 − 2 = 2 cm. Portanto a sua área é
2
(5 + 9) ⋅
= 14 cm 2 .
2
Questão 2
Observe atentamente as figuras de uma pá e
calcule a e b, admitindo que os valores numéricos no plano cartesiano estão em centímetros.
Pela figura planificada, PQ = RT = a e a distância
de S a PR é b.
Pelo gráfico, os pontos T e S têm coordenadas
(3,5; a) e (0; b), respectivamente, para a e b positivos. Como T e S pertencem ao gráfico de
y = −x 2 + 20, temos a = −(3,5) 2 + 20 ⇔
⇔ a = 7,75 cm e b = −0 2 + 20 ⇔ b = 20 cm.
Questão 3
Os dados da tabela foram obtidos a partir de
um estudo realizado com 9 800 indivíduos da
mesma faixa etária.
Não
Pratica
Pratica
pratica Total
exercícios
exercícios
regularmente irregularmente exercícios
Possui
doença
cardíaca
95
297
712
1 104
Não
possui
doença
cardíaca
891
6 811
994
8 696
Total
986
7 108
1 706
9 800
matemática
Sorteando-se ao acaso um indivíduo dentre os
pesquisados, calcule a probabilidade de que
ele seja portador de doença cardíaca, apesar
de praticar regularmente ou irregularmente
exercícios. O resultado do seu cálculo deve
ser dado em porcentagem.
Questão 5
As figuras mostram um cone circular reto de
raio da base r e a planificação da sua área
lateral.
Resposta
Da amostra, dos 986 + 7 108 = 8 094 indivíduos
que praticam exercícios regular ou irregularmente,
95 + 297 = 392 têm problemas cardíacos. Assim,
a probabilidade pedida é:
392
≅ 0,0484 = 4,84%
8 094
Questão 4
O segmento AB é simultaneamente diâmetro
de um círculo de raio 2 e lado do triângulo
eqüilátero ABC. O círculo intersecta os segmentos AC e BC nos pontos D e E, respectivamente. Faça uma figura representando a
situação descrita e calcule o comprimento do
segmento AE.
Resposta
Consideremos a figura a seguir, em que AB é o
diâmetro da circunferência de raio 2 e ABC é o
triângulo eqüilátero de lado 4.
Relembrando que o volume de um cone é
1
igual a do produto entre a área da base e a
3
altura do cone, calcule o raio da base e o volume desse cone.
Resposta
Pelo teorema do ângulo inscrito numa circunfe$
rência, m (AEB)
= 90o e, assim, AE é altura do
4⋅ 3
triângulo eqüilátero ABC, cuja medida é
=
2
=2 3.
270o
9
cm. O
⋅ 2 ⋅ π ⋅ 3 ⇔r =
4
360o
raio do setor circular da planificação da área lateral do cone é igual a sua geratriz, ou seja,
g = 3 cm.
Temos 2 ⋅ π ⋅ r =
matemática
mais uma pessoa no grupo, a nova média
passou a ser 26 anos. Determine a idade do
novo integrante do grupo em função de x.
Resposta
A soma das idades do grupo de x pessoas é 25x
anos. Após a entrada de mais uma pessoa a
soma passa a ser 26(x + 1) anos.
Logo a idade do novo integrante do grupo é, em
anos, 26(x + 1) − 25x = x + 26.
Questão 8
Sendo h a altura do cone, aplicando o Teorema
2
⎛9 ⎞
de Pitágoras ao ΔABC, temos h 2 + ⎜ ⎟ = 3 2 ⇔
⎝4⎠
3 7
cm.
⇔h =
4
Assim, o volume do cone é dado por
2
1
3 7
81 7 π
⎛9 ⎞
π⋅⎜ ⎟ ⋅
=
cm 2 .
⎝4⎠
3
4
64
Sobre a figura, sabe-se que:
Questão 6
⎧p ⋅ x − y = 2
No sistema de equações ⎨
⎩(p + q) ⋅ x + y = 3
p e q são constantes reais e x e y são variáveis
reais.
Calcule p e q, sabendo-se que a solução desse
sistema é o par ordenado (2, −3).
Resposta
Como o par ordenado (2; −3) é solução desse sistema:
p ⋅ 2 − ( −3) = 2
2p + 3 = 2
⇔
⇔
(p + q) ⋅ 2 − 3 = 3
p +q =3
⇔
p =−
1
2
7
2
Pode-se verificar que (2; −3) é, realmente, a única
solução do sistema.
q =
Questão 7
A média aritmética das idades de um grupo
de x pessoas é 25 anos. Com a entrada de
•
•
•
ABC e EFD são triângulos;
os pontos A, C, D e E estão alinhados;
a reta que passa por B e C é paralela à reta
que passa por D e F;
$ e DFE
$ são congruentes;
• os ângulos ABC
• AB = 5 cm, AC = 6 cm, EF = 4,8 cm e AE =
= 10 cm
Calcule a medida do segmento CD.
Resposta
Já que FD // BC, os ângulos alternos internos
$ e BCA
$ são congruentes. Considerando ainda
FDE
$ e DFE
$ são congruentes, pelo
que os ângulos ABC
caso AA, ΔFDE ~ ΔBCA.
Sendo DC = x e CE = 10 − 6 = 4 cm, então
FE
DE
4,8
4 +x
DE = 4 + x . Logo
=
⇔
=
⇔
BA
CA
5
6
⇔ x = 1,76 cm.