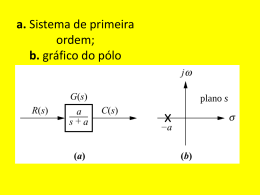
Análise de Resposta Transitória e de
Regime Estacionário
5.1 Introdução
5.2. Sistemas de Primeira Ordem
5.3. Sistemas de Segunda Ordem
Prof. André Marcato
Livro Texto: Engenharia de Controle Moderno – Quarta Edição –
Editora Pearson Prentice Hall – Autor: Katsuhiko OGATA
1
Introdução


Análise de um sistema de controle:

Obtenção de um modelo matemático

Analisar o desempenho do sistema a partir de vários
métodos disponíveis
Sinais de Entrada


Aula 13
Geralmente, não são conhecidos previamente
Análise e projeto de sistemas de controle

Deve-se ter uma base de comparação de desempenho
de vários sistemas de controle

Deve-se detalhar os sinais de teste da entrada frente
aos diversos tipos de sistemas de controle
Sinais Típicos de Teste

Sinais de teste geralmente utilizados:


Determinação dos sinais típicos de teste:



Aula 13
Funções degrau, rampa, parábola de aceleração,
impulso, senoidal
Análise do comportamento da entrada que o sistema
será submetido com maior freqüência sob condições
normais de operação.
Se são funções de tempo que variam gradualmente:
rampa
Se o sistema está sujeito a variações bruscas na
entrada: impulso
Resposta Transitória e Resposta
Estacionária
Resposta Transitória: Vai do
estado inicial ao estado final.
Resposta Estacionária:
Comportamento da saída do sistema
à medida que t tende ao infinito
Também chamada de
Solução Homogênea
Também chamada de
Resposta Forçada ou
Solução Particular
Resposta do Sistema
Aula 13
Pólos de Uma Função de
Transferência
Aula 13
1.
Valores da variável complexa, s,
da Transformada de Laplace, que
levam o valor da função de
transferência tender ao infinito
2.
Quaisquer raízes do denominador
da função de transferência que
são comuns às raízes do
numerador
Zeros de Uma Função de
Transferência
Aula 13
1.
Os valores da variável complexa,
s, da Transformada de Laplace
que anulam o valor da função de
transferência
2.
Quaisquer raízes do numerador da
função de transferência que são
comuns às raízes do denominador.
Estabilidade Absoluta de Um Sistema de
Controle Linear, Invariante no Tempo

Previsão do comportamento dinâmico do
sistema, a partir do conhecimento de
seus componentes

Estabilidade Absoluta: O sistema é
estável ou instável?


Aula 13
Sistema está em equilíbrio se, na ausência
de qualquer distúrbio ou sinal de entrada, a
saída permanece no mesmo estado
Sistema é estável se a saída sempre retorna
ao estado de equilíbrio quando o sistema é
submetido a uma condição inicial
Estabilidade Relativa de um Sistema de
Controle Linear, Invariante no Tempo
Aula 13

O sistema será criticamente estável se as
oscilações do sinal de saída se repetirem de
maneira contínua

O sistema será instável se a saída divergir sem
limites a partir do estado de equilíbrio quando o
sistema for sujeito a uma condição inicial

Nos casos reais, o sinal de saída de um sistema
físico pode aumentar até certo valor, mas pode
ser limitado por fins de curso mecânico, ou o
sistema pode se romper, ou se tornar não
linear, etc.
Estabilidade Relativa e Erro
Estacionário

Devido a energia armazenada no sistema, a
saída do mesmo não segue imediatamente a
entrada.

Aula 13
Apresenta uma resposta transitória antes que o
regime permanente seja obtido

A resposta transitória, geralmente, apresenta
oscilações amortecidas antes de atingir o
estado permanente.

Se o sinal de saída permanente não
corresponder exatamente ao sinal de entrada,
diz-se que o sistema apresenta um erro
estacionário. O erro estacionário deve sempre
ser avaliado na análise de sistemas de controle.
Sistemas de Primeira Ordem
São sistemas diferenciais que envolvem apenas
a primeira derivada da saída na sua equação.
Aula 13
Sistemas de Primeira Ordem
Resposta ao Degrau Unitário
A Transformada de
Laplace da Função
Degrau Unitário é 1/s
Aula 13
Sistemas de Primeira Ordem
Resposta ao Degrau Unitário
Aula 13
Sistemas de Primeira Ordem
Resposta à Rampa Unitária
A Transformada de
Laplace da Função
Rampa é 1/s2
Aula 13
Sistemas de Primeira Ordem
Resposta à Rampa Unitária
Aula 13
Sistemas de Primeira Ordem
Resposta ao Impulso Unitário
Aula 13
Propriedade Importante de Sistemas
Lineares Invariantes no Tempo
Aula 13
Pólos e Zeros de Um Sistema de
Primeira Ordem – Um Exemplo (1)
Aula 13
Pólos e Zeros de Um Sistema de
Primeira Ordem – Um Exemplo (2)
Aula 13
Pólos e Zeros de Um Sistema de
Primeira Ordem – Um Exemplo (3)
Um
pólo
sobre
o eixo
real
gera
uma
resposta
exponencial
da
forma
e-αt,
da função
entrada
gera
agera
forma
da resposta
forçada
(isto
OsUm
zeros
pólo
e pólos
na
geram
deas
transferência
amplitudes
tanto
apara
forma
a resposta
da resposta
forçada
natural
onde
–α, éé,apara
pólo
sobre
opode
eixoa ser
real.
Assim
olocalização
pólo
na origem
gerou
uma
função
degrau
saída.
quanto
a(isto
resposta
é, do
o pólo
natural
em
(isto
-5
gerou
função
percebido
e-5tna
) quanto
pelosmais à
esquerda no eixo real
negativo,
cálculos
deestiver
A1 e A2 um pólo, mais rápido o
decaimento da resposta transiente exponencial para zero.
Aula 13
Funções de Primeira Ordem
Obtidas Experimentalmente
Características de um
sistema de primeira
ordem:
1) Não presença de sobrevalor
2) inclinação inicial não
nula.
Aula 13
Sistemas de Segunda Ordem (1)
São sistemas diferenciais que envolvem apenas a
primeira e a segunda derivada da saída na sua equação.

Aula 13
Enquanto a variação de um parâmetro
no sistema de primeira ordem
simplesmente altera a velocidade da
resposta, as variações nos parâmetros
de um sistema de segunda ordem
podem alterar a forma da resposta.
Sistemas de Segunda Ordem (2)
Aula 13
Sistemas de Segunda Ordem (3)
Aula 13
Sistemas de Segunda Ordem (4)
Aula 13
Resposta Superamortecida

1 Pólo na origem: Entrada Degrau Unitário → Gera Resposta
Forçada

2 Pólos Reais: Decorrentes do Sistema → Gera Resposta
Natural
Aula 13
Resposta Subamortecida

1 Pólo na origem: Entrada Degrau Unitário → Gera
Resposta Forçada

2 Pólos Complexos:
→ Gera Resposta Natural
Aula 13
Decorrentes do Sistema

Parte Real: Freqüência de decaimento exponencial (inverso
da parte real do polo)

Parte Imaginária: Freqüência de oscilação senoidal
Resposta Não Amortecida

1 Pólo na origem: Entrada Degrau Unitário → Gera
Resposta Forçada

2 Pólos Complexos:
Resposta Natural
Aula 13
Decorrentes do Sistema → Gera

Parte Real: Nula. Exponencial que não apresenta
decaimento.

Parte Imaginária: Freqüência de oscilação senoidal
Resposta Criticamente Amortecida

1 Pólo na origem: Entrada Degrau Unitário → Gera
Resposta Forçada

2 Reais e iguais (coordenada -3). Geram uma
exponencial simples e uma exponencial multiplicada pelo
tempo.

São as repostas mais rápidas possíveis sem ocorrência
de sobrevalor.
Aula 13
Resposta ao Degrau para os Casos de
Sistemas de Segunda Ordem Amortecidos
Aula 13