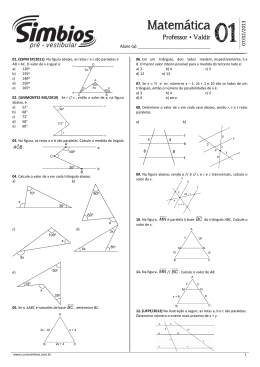
Aluno (a):
01. (ESPM SP/2011) Na figura abaixo, as retas r e s são paralelas e
AB = AC. O valor de x é igual a:
a) 120°
b) 135°
c) 140°
d) 150°
e) 165°
02. (UNIMONTES MG/2010) Se r // s , então o valor de x, na figura
abaixo, é
a) 52°
b) 68°
c) 72°
d) 58°
e) 60°.
3 º ANO
4
1
Professor • Valdir
Ângulos, triângulos e paralelismo
23/02/2013
Matemática
06. Em um triângulo, dois lados medem, respectivamente, 5 e
8. O menor valor inteiro possível para a medida do terceiro lado é:
a) 3
b) 4
c) 5
d) 12
e) 13
07. Se x ∈ Ν e os números x – 1, 2x + 1 e 10 são os lados de um
triângulo, então o número de possibilidades de x é:
a) 3
b) 4
c) 5
d) 6
e) zero
08. Determine o valor de x em cada caso abaixo, sendo r, s e t retas
paralelas.
r
a)
b)
5
s
r
x
6
4
3
s
x
2
y
8
t
6
t
03. Na figura, as retas a e b são paralelas. Calcule a medida do ângulo
A
ˆ .
ACB
a
140o
09. Na figura abaixo, sendo a // b // c e r e s transversais, calcule o
a
valor de x.
C
30o
b
b
B
c
04. Calcule o valor de x em cada triângulo abaixo.
a)
b)
3
2x - 1
4
50o
70o
x+1
x
30o
10. Na figura, MN é paralela à base BC do triângulo ABC. Calcule o
valor de x.
A
60o
x
c)
x
d)
100o
30
M
3x
N
10
12
B
C
x
5x
3x
80o
11. Na figura, MN//BC. Calcule o comprimento de AB.
A
x
M
o
50
3
N
e)
x+6
6
15o
x
B
35o
C
12. (UFPE/2012) Na ilustração a seguir, as retas a, b e c são paralelas.
Determine número o inteiro mais próximo de x + y.
05. Se o ∆ABC é isósceles de base BC, determine BC.
A
3x - 10
B
www.cursosimbios.com.br
x+4
2x + 4
C
1
13. (FATEC SP) O dobro da medida do complemento de um ângulo
o
aumentado de 40 é igual à medida do seu suplemento. Determine a
medida desse ângulo.
14. (UEG GO/2010) A figura abaixo representa o disparo de um
projétil de arma de fogo a partir de dois pontos distintos, A e B. Em
ambos os casos, eles colidem com um anteparo rígido e são
ricocheteados em um ângulo θ1 de 7°. O valor do ângulo θ2, em
graus, é:
a) 173
b) 83
c) 28
d) 7
20. Num triângulo ABC, os ângulos B̂ e Ĉ medem 50º e 70º,
respectivamente. A bissetriz relativa ao vértice A forma com a reta
BC ângulos proporcionais a:
a) 1 e 2
b) 2 e 3
c) 3 e 4
d) 4 e 5
e) 5 e 6
21. A figura abaixo é a representação de seis ruas de uma cidade. As
ruas R1, R2 e R3 são paralelas entre si. Paulo encontra-se na posição
A da rua R1 e quer ir para a rua R2 até a posição B. Se a escala de
representação for de 1 : 50 000, a distância, em metros, que Paulo
vai percorrer será de, aproximadamente,
a) 1 333.
b) 750.
c) 945.
d) 3 000.
15. (UECE) Considere 5 semi-retas, todas partindo do mesmo ponto
P num certo plano, formando 5 ângulos contíguos que cobrem todo o
plano, cujas medidas são proporcionais aos números 2, 3, 4, 5 e 6.
Determine a diferença entre o maior e o menor ângulo.
a) 22°
b) 34°
c) 56°
d) 72°
e) 36°
16. No desenho abaixo estão representados os terrenos I, II e III.
Determine, usando o teorema de Tales, o comprimento do muro que
o proprietário do terreno II deverá construir para fecha o lado que faz
frente com a rua das Rosas.
22. Dados dois ângulos adjacentes, a medida de um deles é o triplo
da medida do outro. A medida do complemento do ângulo entre as
suas bissetrizes é 50º. Determine a medida do complemento da soma
dos ângulos dados.
ˆ e AEC
ˆ têm os lados, respectivamente,
23. Na figura, os ângulos ABC
ˆ igual a 40º, calcule
perpendiculares. Sendo a medida do ângulo ABC
E
ˆ
a medida do ângulo AEC
A
17. Determine a medida do ângulo do vértice P do triângulo isósceles
PQR de base QR, sabendo que os segmentos PS, ST, TU, UQ e QR são
congruentes.
Q
T
B
C
24. Com os dados fornecidos na figura, determine a medida do
ângulo a.
P
r // s
35o
a
x
S
U
R
18. No triângulo ABC da figura, se AH é altura e BS bissetriz interna,
determine a medida do ângulo x. A
30º
s
25. A figura abaixo mostra um triângulo ABC, isósceles de base BC.
S
x
ˆ calcule o valor de
ˆ e CI bissetriz de ACB
Sendo BI bissetriz de ABC
x.
A
40º
B
a+x
80o
C
H
80°
19. No triângulo ABC da figura, se AH é altura e BS é bissetriz,
ˆ dados BÂH = 30º e ACB
ˆ = 40°.
determine BSC
I
x
A
C
B
30o
S
x
40o
B
www.cursosimbios.com.br
H
C
01) C
02) C
d) 10°; e) 100°
08) a)3; b) 10/3 e 18/5
12) 26
13) 40°
17) 20°
18) 110°
22) 10°
23) 40°
03) 70º
05) 18
09) 7/2
14) A
19) 110°
24) 32,5°
04) a) 100°; b) 110°; c) 50°;
06) B
07) B
10) 25
11) 18
15) D
16) 32m
20) D
21) A
25) 130°
2