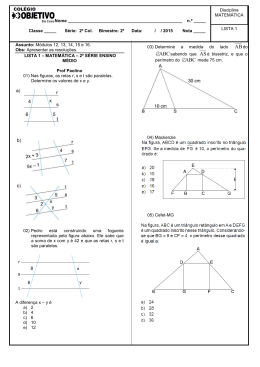
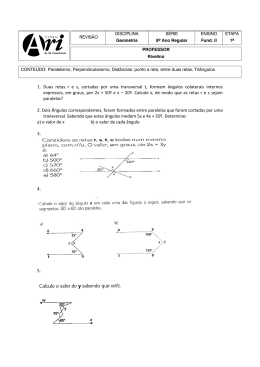
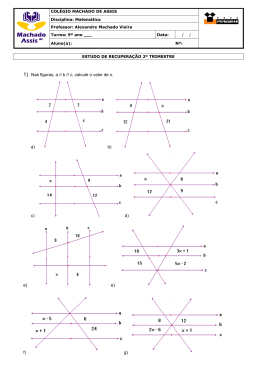
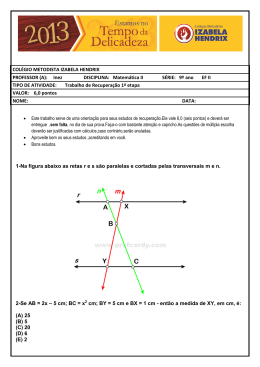
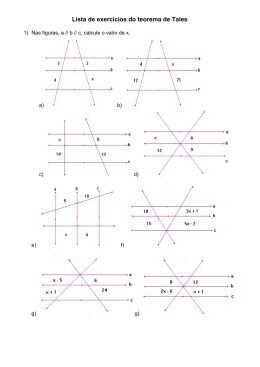
Lista 2 – Teorema de Tales e MDC – 9º ANO – 2014
4. No triângulo ABC da figura, AB = 24 cm e AC = 32 cm. A partir do vértice A, sobre a reta
suporte do lado AB, marca-se AE = 9 cm, e, sobre a reta suporte do lado AC, marca-se AD
= x cm. Determine o valor de x, de modo que a reta DE seja paralela à reta BC. (x = 12 cm)
1. Em cada uma das figuras, as retas r e s são transversais às retas a, b e c de um feixe de
retas paralelas. Calcule o valor de x. (a) x = 10 b) x = 3)
5. Num triângulo ABC, AB = 20 cm e AC = 28 cm. Por um ponto D, sobre o lado AB e
distante 5 cm do vértice A, traça-se o segmento DE, paralelo ao lado BC e com o ponto E
sobre o lado AC. Calcule a medida do segmento AE. (7 cm)
6. (FAAP) O proprietário de uma área quer dividi-la em três lotes, conforme a figura abaixo.
Determine os valores de a, b e c, em metros, sabendo-se que as laterais dos terrenos são
paralelas e que a + b + c = 120m. (a = 30 cm, b = 36 cm e c = 54 cm)
2. Na figura, DE é paralelo ao lado BC do triângulo ABC. Calcule o valor de x. (x = 2)
3. Na figura, as retas r e s são transversais às retas a, b, c e d de um feixe de retas
paralelas. Calcule x, y e z, sabendo-se que AB = 33 cm. (x = 6 cm, y = 12 cm, z = 15 cm)
7. (UNICAMP) A figura a seguir mostra um segmento AD dividido em três partes: AB = 2
cm, BC = 3 cm e CD = 5 cm. O segmento AD’ mede 13 cm e as retas BB’ e CC’ são
paralelas a DD’. Determine os comprimentos dos segmentos AB’, B’C’ e C’D’ em
centímetros. (2,6 cm, 3,9 cm, 6,5 cm respectivamente)
8. Um feixe de paralelas determina sobre uma transversal t 1 os segmentos AB e BC, tais
que AB = (x + 1) cm e BC = (x + 8) cm. O mesmo feixe determina sobre uma segunda
transversal t2 os segmentos EF e FG tais que EF = (x + 10) cm e FG = (x + 20) cm; os
pontos A e E estão alinhados. Qual é o valor da soma AB + BC + EF + FG? (119 cm)
9. (MACK) Na figura, sendo a // b // c, determine o valor de x. (R. x = 2)
10. Na figura DE // BC. Determine o valor de x (R. x = 10)
11. Duas avenidas se cruzam em um ponto A. Essas avenidas cortam três ruas, r 1, r2 e r3,
que são paralelas entre si. Os segmentos AD, AB e BC representam quarteirões da
Avenida 2, enquanto os segmentos AM, AN e NP representam quarteirões da Avenida 1.
Na figura estão indicados os comprimentos, em metros, desses quarteirões. Determine os
comprimentos dos quarteirões representados pelos segmentos BC e AM. (138 cm e 37,5
cm)
12. Dois lotes estão representados na figura abaixo. Calcular as medidas de frente para a
rua R de cada um dos terrenos, respectivamente. (22 m e 33 m)
13. A figura abaixo nos mostra dois terrenos cujas laterais são paralelas. De acordo com a
figura, determine as medidas x e y. (x = 18 m e y = 45 m)
14. Uma reta paralela ao lado BC de um triângulo ABC determina o ponto D em AB e E em
AC. Sabendo – se que AD = x, BD = x + 6, AE = 3 e EC = 4, determine o lado AB do
triângulo. (AB = 42)
15. No piso de uma sala com 3,36m de largura e 4,00m de comprimento, um construtor
deseja colocar peças de granito quadradas, do mesmo tamanho. Determine a menor
quantidade dessas peças que ele pode usar para cobrir completamente o piso. (525 pisos)
16. Uma faixa retangular de tecido deverá ser totalmente recortada em quadrados, todos de
mesmo tamanho e sem deixar sobras. Esses quadrados deverão ter o maior lado possível.
Se as dimensões da faixa são 105 cm de largura por 700 cm de comprimento, calcule o
perímetro de cada quadrado, em centímetros. (20 cm)
17. Os alunos do 9º ano do Colégio Singular Júnior vão fazer a viagem de formatura no
final do ano. O hotel escolhido aceita reservas sob a seguinte condição: cada quarto deve
apresentar exatamente o mesmo número de hóspedes e as turmas não podem ser
misturadas. Sabendo que irão 40 alunos da 9J1, 28 da 9J3 e 36 da 9J5 e que cada quarto
apresentará o maior número possível de alunos, quantos alunos se hospedarão no mesmo
quarto? (4 alunos)
18. No 1° ano do ensino médio existem 120 alunos, no 2° ano existem 135 alunos e no 3°
ano existem 90 alunos. Para a realização de um evento essas turmas precisam se
organizar em grupos iguais, com o maior número possível de alunos por grupo. Quantos
grupos serão formados no total? (23 grupos)