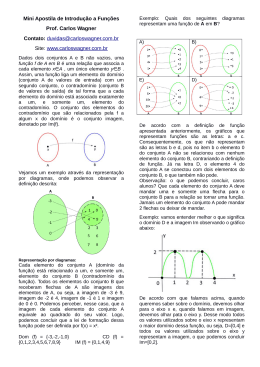
Funções e Gáficos
2a aula – Profa. Marli
Sumario
•
•
•
•
•
•
•
Definição de funções
Domínio e Contradomínio
Função definida ou não definida em uma variável
Variável dependente e independente
Imagem
Gráfico de uma função
Operações entre funções
Funções
• Função é uma relação que associa cada
elemento de um conjunto numérico a um
único elemento de um outro conjunto
numérico.
• Exemplo:
100.8
3.9
-3.9
6.0
40.9
Conjunto D
7.8
12.0
201.6
15.0
12.9
81.8
Conjunto C
Definição- função
• Seja A e B subconjuntos de R .
• Uma função f:AB é uma regra que cada
elemento de A faz correspondência a um
único elemento de B.
• O conjunto A é chamado domínio de f e é
denotado por Dm(f).
• O conjunto B é chamado de
contradomínio ou campo de valores de f.
Escrevemos
f: A B
x f(x)
ou
f
A B
x y = f(x).
f: A B ( é função)
v
A - Domínio
B - Contradomínio
g: A B ( não é função)
v
A
B
h: A B ( não é função)
v
A
B
Função definida ou não definida
em uma variável
• Se x está no domínio, dizemos que f e definida
em x, ou que f(x) existe.
• Se x não está no domínio, dizemos que f e não é
definida em x, ou que f(x) existe.
• Exemplo: Para f ( x)  x  2 ,o domínio é o
intervalo [2,+).
Podemos dizer que f é definida em x pertencente
ao intervalo [2,+) e f é não definida em x
pertencente ao intervalo (-,2).
Variável dependente e
independente
• Seja f: A B
x y = f(x)
x  A (domínio de f), x é uma variável
independente,
x reapresenta um número arbitrário do domínio.
y  B (contradomínio de f), y é uma variável
dependente,
pois y depende de x.
Definição - imagem
• Seja f: A B.
• Dado x  A, o elemento é chamado o valor
da função f no ponto x ou imagem de
x por f.
• O Conjunto de todos os valores assumidos
pela função é chamado de conjunto
imagem de f e é denotado por Im(f).
Gráficos de uma função
• Seja f uma função . O gráfico de f é o
conjunto de todos os pontos (x,f(x)) de um
plano coordenado, onde x pertence ao
domínio de f.
• Exemplo: seja y = f(x) = 2x2
•Exemplo: seja y = f(x) = 2x2
x
y = f(x)
-2.0
8.0
-1.5
4.5
-1.0
2.0
-0.5
0.5
0.0
0.0
0.5
0.5
1.0
2.0
1.5
4.5
2.0
8.0
Operações - soma, diferença,
produto e quociente
• Dadas as funções f e g, sua soma f + g,
diferença f - g, produto f . g e quociente
f / g, são definidas por
• (f+g)(x) = f(x)+g(x)
• (f - g)(x) = f(x) - g(x)
• (f.g)(x) = f(x).g(x)
• (f/g)(x) = f(x)/g(x)
Domínio
f+g, f-g, e f.g e f/g
• O domínio das funções f+g, f-g, e f.g, é a
interseção dos domínios de f e g.
• O domínio das funções f/g é a interseção
dos domínios de f e g, excluindo-se os
pontos x onde g(x) =0.
Operação -kf
• Se f é uma função e k é um número real,
definimos a função kf por
• (kf)(x) = kf(x).
• O domínio de kf coincide com o domínio
de f .
Operação função composta
• Dadas duas funções f e g , a função
composta de g com f, denotada por g0 f, é
definida por
• (g0 f) (x) = g(f(x)).
• O domínio de g0 f é o conjunto de todos os
pontos x no domínio de f tais que f(x) está
no domínio de g.
Simbolicamente
• Dm(g0 f) = {xDm(f) / f(x)  Dm(g)}.
• Em diagrama
f
g
x
f(x)
g0 f
g(f(x))
Exemplo
• Seja f ( x)  x e
Encontramos gof.
g ( x)  x .1
( go f )  g ( f ( x))  g ( x )  x 1.
Dm(f) = [0,+) e Im(f ) = [0,+).
Dm(g) = (-, ) e Im(g) = (-, ).
Im(f )  Dm(g).
Dm(g0 f) = {xDm(f) / f(x)  Dm(g)}= [0,+).
Exemplo
• Seja f ( x)  x e
Encontramos fog.
g ( x)  x  1.
( fo g )  f ( g ( x))  f ( x 1)  x 1.
Dm(f) = (0,+) e Im(f) = (0,+)
Dm(g) = (- , +) e Im(g) = (- , +)
Dm(fog) = {xDm(g) / g(x)  Dm(f)}= [1,+).
Isso porque, x-1  Dm(f) = (0,+) ou seja x-10
ou x 1.