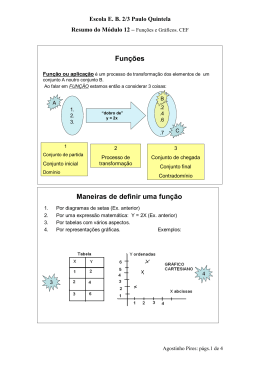
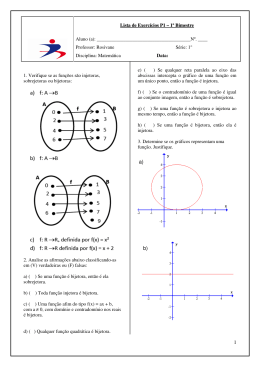
Mini Apostila de Introdução a Funções
Prof. Carlos Wagner
Contato: [email protected]
Exemplo: Quais dos seguintes diagramas
representam uma função de A em B?
A)
B)
E)
D)
Site: www.carloswagner.com.br
Dados dois conjuntos A e B não vazios, uma
função f de A em B é uma relação que associa a
cada elemento x∈A , um único elemento y∈B .
Assim, uma função liga um elemento do domínio
(conjunto A de valores de entrada) com um
segundo conjunto, o contradomínio (conjunto B
de valores de saída) de tal forma que a cada
elemento do domínio está associado exatamente
a um, e somente um, elemento do
contradomínio. O conjunto dos elementos do
contradomínio que são relacionados pela f a
algum x do domínio é o conjunto imagem,
denotado por Im(f).
Vejamos um exemplo através da representação
por diagramas, onde podemos observar a
definição descrita:
De acordo com a definição de função
apresentada anteriormente, os gráficos que
representam funções são as letras: a e c.
Consequentemente, os que não representam
são as letras b e d, pois no item b o elemento 0
do conjunto A não se relacionou com nenhum
elemento do conjunto B, contrariando a definição
de função. Já na letra D, o elemento 4 do
conjunto A se conectou com dois elementos do
conjunto B, o que também não pode.
Observação: o que podemos concluir, caros
alunos? Que cada elemento do conjunto A deve
mandar uma e somente uma flecha para o
conjunto B para a relação se tornar uma função.
Jamais um elemento do conjunto A pode mandar
2 flechas ou deixar de mandar.
Exemplo: vamos entender melhor o que significa
o domínio D e a imagem Im observando o gráfico
abaixo:
Representação por diagramas:
Cada elemento do conjunto A (domínio da
função) está relacionado a um, e somente um,
elemento do conjunto B (contradomínio da
função). Todos os elementos do conjunto B que
receberam flechas de A são imagens dos
elementos de A, ou seja, a imagem de -3 é 9,
imagem de -2 é 4, imagem de -1 é 1 e imagem
de 0 é 0. Podemos perceber, nesse caso, que a
imagem de cada elemento do conjunto A
equivale ao quadrado do seu valor. Logo,
podemos concluir que a lei de formação dessa
função pode ser definida por f(x) = x².
Dom (f) = {-3,-2,-1,0}
{0,1,2,3,4,5,6,7,8,9}
CD (f) =
IM (f) = {0,1,4,9}
De acordo com que falamos acima, quando
queremos saber sobre o domínio, devemos olhar
para o eixo x e, quando falamos em imagem,
devemos olhar pata o eixo y. Desse modo todos
os valores utilizados sobre o eixo x representam
o maior domínio dessa função, ou seja, D=[0,4] e
todos ou valores utilizados sobre o eixo y
representam a imagem, o que podemos concluir
Im=[0,2].
Exemplo: vamos determinar o maior domínio
das funções abaixo:
1º) f(x) =3x
Sabemos que o denominador de uma fração tem
que ser diferente de zero, pois não existe divisão
por zero. Nesse caso, temos que ter x≠ 0 para
que 2x seja possível em IR. Logo o domínio são
os reais não nulos.
2º) f(x) = √ x − 4
Sabemos que no conjunto dos números reais
não existe raiz quadrada de número negativo.
Portanto, temos que ter x−4≥0 para que seja
possível em IR. Daí, x−4≥0⟺x≥4
Logo, D(f) = [4, + ∞[.
3º) f(x) =
Sendo assim, é possível observar facilmente a
lei de formação dessa função. O total (y) a ser
pago será R$ 1,75 multiplicado pela quantidade
(x) de picolés. Logo, podemos concluir que y =
1,75.x.
Observação:
Seja f : R → R uma função. Tal representação
pode ser descrita por D → CD onde D são os
elementos do domínio e CD elementos do
contradomínio. Sendo I o conjunto imagem,
podemos dizer que I é subconjunto de CD, ou
seja, I⊂ CD.
Classificação de uma função:
As funções podem ser classificadas em injetora
ou injetiva, sobrejetora ou sobrejetiva e bijetora
ou bijetiva. Uma função é:
√1 − x
x −2
Nesse caso, devemos ter:
(I) 7−x≥0⟺−x≥−7⟺x≤7
(II) x−2>0⟺x>2
- Injetora ou injetiva quando, para quaisquer
elementos x1 ≠ x2 , temos f(x1) ≠ f(x2 );

Exemplo:
Ou seja, x ∈ ]2, 7]. Para cada x ∈ ]2, 7], f(x)
existe e é único.
Logo, D(f) = ]2, 7].
Vamos observar agora mais um exemplo
cotidiano onde a função se faz presente:
Uma barraca de praia, em Salvador, vende
picolés ao preço de R$ 1,75 a unidade. Para não
precisar fazer contas a todo momento, o
proprietário da barraca montou a seguinte tabela:
Número de picolés
1
2
3
4
5
6
7
8
Preço (R$)
1,75
3,50
5,25
7,00
8,75
10,50
12,25
14,00
Note que o número de picolés é o domínio da
função, e o preço correspondente à quantidade
de picolés, o contradomínio. Logo, podemos
observar que:
Dom (f) = {0,1,2,3,4,5,6,7,8}
CD (f) = {1,75; 3,50; 5,25; 7. 8,75; 10,5; 12,25;
14}
Im (f) = {1,75; 3,50; 5,25; 7. 8,75; 10,5; 12,25;
14}
Como todos os elementos do contradomínio são
imagens, podemos concluir que o conjunto
imagem é igual ao conjunto contradomínio.
- Sobrejetora ou sobrejetiva quando o conjunto
imagem for igual ao conjunto do contradomínio,
ou seja, possuem os mesmos elementos;
Exemplo:
- Bijetora ou bijetiva quando ela for injetora e
sobrejetora simultaneamente.
Exemplo:
Trabalho de Introdução a Funções [_,_]
b) g(x) = x2 + 1
Nome:_____________ N0:____Turma:___
1.
[0,5]
Dada
a
função
, definida pela
fórmula f(x)=2x²+1. Represente através
de notação de conjuntos: Domínio,
Contradomínio e a Imagem.
5. [0,5] Estude o Domínio de cada função
abaixo:
A)
2. [0,5] Dado o esquema abaixo,
representando uma função de "A" em
"B", determine:
B)
a) O Domínio:
d) f(12)
b) A imagem
c) f(5)
3. [0,5] Quais dos diagramas a seguir se
encaixa na definição de função de A em B,
onde A={a,b,c} e B={1,2,3}. Justifique.
6. [0,5] Observe cada diagrama e classifique
como: Injetora, Sobrejetora ou Bijetora:
a)
b)
c)
4. [0,5] Construa o gráfico de cada função
abaixo:
a) f(x) = 2.x – 1