Escola Secundária de Alves Redol de Vila Franca de Xira
Disciplina de Matemática A – 11º Ano – Tema: Função Racional
1. De uma função quadrática sabe-se que o conjunto solução da inequação
Qual é o contradomínio de
].
[.
[
(A) ]
(B) [
(C) [
(D) ]
é o intervalo [
]
]
2. De uma função g, de domínio IR, sabe-se que:
 g 0  1 ;
 g é estritamente crescente em 0; ;
 g é par.
Indique das seguintes afirmações é verdadeira:
(A) O contradomínio de g é 0; ;
(C) g é injectiva;
(B) g é uma função estritamente
(D) g não tem zeros.
crescente em IR;
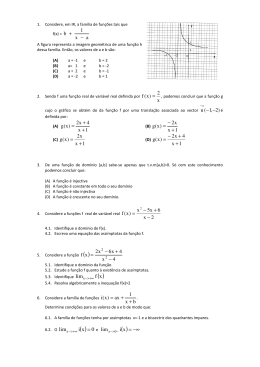
3. O gráfico da função f, representada na figura , tem por assímptotas as rectas x  1 e y  2 . Qual das
expressões analíticas pode definir f x  ?
(A) f x   2 
(C) f x  
4. Seja
2x
x 1
2
x 1
(B) f x  
 2x
x 1
(D) f x  
x
x 1
uma função de domínio ℝ, estritamente crescente.
Qual das seguintes afirmações é necessariamente verdadeira?
(A) A função não pode ter mais do que um zero.
(B) A função tem contradomínio ℝ.
(C) O gráfico da função tem a concavidade voltada para cima.
(D) O gráfico da função é simétrico em relação ao eixo das ordenadas.
Prof. Vânia Santos
5. Seja
uma função de domínio ℝ e contradomínio [
Qual é o contradomínio de | |?
]
(A) [ ]
(B) [
(C) [
]
]
(D) [
]
(D) {
}
6. De uma função , de domínio ℝ, sabe-se que:


é uma função par.
Seja a função, de domínio ℝ, definida por
Qual dos seguintes pode ser o conjunto dos zeros de
(A) {
}
(B) {
7. Considere a função
}
(C) {
}
de domínio ℝ { } definida por
7.1. Sem recorrer à calculadora, determine o conjunto solução dos números reais
Apresente a resposta final na forma de intervalo (ou união de intervalos).
7.2. O gráfico da função
tais que
tem duas assímptotas. Escreva as suas equações.
8. Na figura está representada, em referencial o.n.
como as duas assímptotas deste gráfico.
parte do gráfico de uma função
Tal como a figura sugere,
 A origem do referencial pertence ao gráfico de
 Uma das assímptotas é paralela ao eixo
 A outra assímptota é paralela ao eixo
e intersecta o eixo
bem
no ponto de abcissa 2.
Seja a função, de domínio ℝ, definida por
8.1. Tendo em conta o gráfico de
e a expressão analítica de
completando a seguinte tabela de variação de sinal:
resolva a inequação
Apresente o conjunto solução da inequação utilizando a notação de intervalos de números reais.
8.2. Admita agora que:
 A assímptota do gráfico de paralela ao eixo das abcissas tem equação

é definida por uma expressão do tipo
onde
números reais.
Indique os valores de e de e determine o valor de
9. Considere a função
de domínio ℝ {
calculadora, resolva os itens seguintes:
} definida por
designam
Sem recorrer à
9.1. Determine o conjunto dos números reais que são soluções da inequação
Apresente a sua resposta utilizando a notação de intervalos de números reais.
9.2. Na figura 3 estão representados, em referencial o.n.



Parte do gráfico da função
As rectas e assímptotas do gráfico de
]
O quadrilátero [
e são os pontos de intersecção do gráfico da função
é o ponto de intersecção das rectas e
é o ponto de intersecção da recta com o eixo
Determine a área do quadrilátero [
]
com os eixos coordenados.