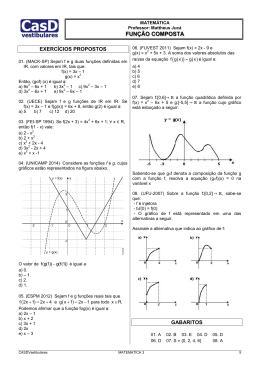
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA
Função Composta
Prof.: Rogério Dias Dalla Riva
Função Composta
1.Função composta
1. Função composta
Seja f uma função de um conjunto A em um
conjunto B e seja g uma função de B em um
conjunto C. Chama-se função composta de g e f à
função h de A em C em que a imagem de cada x é
obtida pelo seguinte procedimento.
1o) aplica-se a x a função f, obtendo-se f(x)
2o) aplica-se a f(x) a função g, obtendo-se g(f(x)).
3
1. Função composta
Indica-se h(x) = g(f(x)) para todo x ∈ A.
Pode-se indicar a composta por g o f (lê-se:
“g composta com f ” ou “g círculo f ”); portanto:
(g o f) (x) = g(f(x))
para todo x ∈ A.
4
1. Função composta
Podemos representar também a composta
g o f pelo diagrama.
A
B
gof
C
5
1. Função composta
Exemplo 1: Sejam os conjuntos A = {-1, 0, 1,
2}, B = {0, 1, 2, 3, 4} e C = {1, 3, 5, 7, 9} e as
funções
f, de A em B, definida por f(x) = x2.
g, de B em C, definida por g(x) = 2x + 1.
6
1. Função composta
h=gof
1
0
3
A
-1
5
1
C
7
2
9
0
1
f
g
2
3
4
B
7
1. Função composta
Observemos por exemplo que: f(2) = 4,
g(4) = 9 e h(2) = 9, isto é, h(2) = (g o f) (2) =
g(f(2)) = g(4) = 9.
Para obtermos a lei de correspondência da
função composta h = g o f, fazemos assim: g(f(x))
é obtida a partir de g(x) trocando-se x por f(x).
No exemplo dado, temos:
h(x) = (g o f) (x) = g(f(x)) = 2 . f(x) + 1 = 2x2 + 1
Se vamos calcular h(2) deste modo:
h(2) = 2 . 22 + 1 = 9
8
1. Função composta
Exemplo 2: Sejam as funções reais f e g definidas
por f(x) = x + 1 e g(x) = x2 + x + 1.
Notemos que a função composta h = g o f é
definida por:
h(x) = (g o f)(x) = g(f(x)) = [f(x)]2] + f(x) + 1 =
(x + 1)2 + (x + 1) + 1 = x2 + 3x + 3.
9
1. Função composta
Observações:
1a) A composta g o f só está definida
contradomínio da f é igual ao domínio
particular, se as funções f e g são de
então as compostas f o g e g o f estão
e são funções de A em A.
quando o
da g. Em
A em A,
definidas
2a) Notemos que, em geral, f o g ≠ g o f, isto é, a
composição de funções não é comutativa.
10
1. Função composta
Pode acontecer que somente
funções f o g ou g o f esteja definida.
uma
das
Assim, no primeiro exemplo, se tentarmos
obter f o g, verificaremos que é impossível, pois:
g é função de B em C mas f não é função de C em A
11
1. Função composta
0
1
B
0
fog
-1
2
1
3
2
4
1
g é função
A
f não é função
3
5
C
7
9
12
1. Função composta
3a) As duas composições f o g e g o f estão
definidas mas f o g ≠ g o f como nos mostra o
segundo exemplo:
(g o f)(x) = x2 + 3x + 2
(f o g)(x) = x2 + x + 2
13