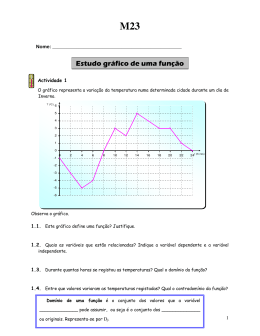
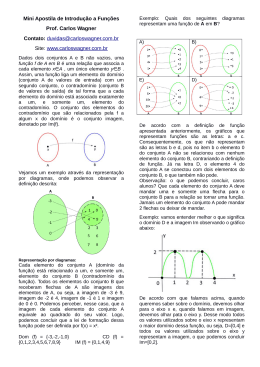
Escola E. B. 2/3 Paulo Quintela
Resumo do Módulo 12 – Funções e Gráficos. CEF
Funções
Função ou aplicação é um processo de transformação dos elementos de um
conjunto A noutro conjunto B.
Ao falar em FUNÇÂO estamos então a considerar 3 coisas:
B
A
1.
2.
3.
“dobro de”
y = 2x
.2
.4
.6
.7
1
Conjunto de partida
Conjunto inicial
Domínio
C
2
3
Processo de
transformação
Conjunto de chegada
Conjunto final
Contradomínio
Maneiras de definir uma função
1.
2.
3.
4.
Por diagramas de setas (Ex. anterior)
Por uma expressão matemática: Y = 2X (Ex. anterior)
Por tabelas com vários aspectos.
Por representações gráficas.
Exemplos:
4
3
Agostinho Pires: págs.1 de 4
Escola E. B. 2/3 Paulo Quintela
Resumo do Módulo 12 – Funções e Gráficos. CEF
Exemplo 2: Y = x2
Gráfico cartesiano
Tabela
Y (Imagem)
10
0
0
8
1
1
2
4
3
9
-1
1
-2
4
-3
9
y y o rd e n a d a s
X (Objecto)
6
4
2
0
-4
-2
0
2
4
2
4
XX abcissas
Exemplo 3: Y = x3
Gráfico cartesiano
Tabela
30
Y (Imagem)
0
0
1
1
2
8
3
27
-1
-1
-2
-8
-3
-27
20
Y Y o rd e n a d as
X (objecto)
10
0
-4
-2
-10
0
-20
-30
XX abcissas
Agostinho Pires: págs.2 de 4
Escola E. B. 2/3 Paulo Quintela
Resumo do Módulo 12 – Funções e Gráficos. CEF
Tipos de funções
1.
Injectivas: Se objectos diferentes possuem sempre imagens
diferentes. Ex: y = 2x e y = x3 (verificar).
2.
Não Injectivas: Se objectos diferentes possuem imagens
iguais. Ex: Y = x2 (verificar)
3.
Sobrejectivas: Se o conjunto final ou de chegada for igual ao
contradomínio (B = C no primeiro diapositivo).
4.
Não sobrejectivas: Se o conjunto final ou de chegada for
diferente do contradomínio (no primeiro diapositivo B é diferente
de C). Significa que todo o elemento do conjunto final é imagem
de algum elemento do conjunto A.
5.
Bijectivas: Se uma função é ao mesmo tempo Injectiva e
Sobrejectiva. Para estas existe sempre uma função Inversa que
transforma B em A.
Exemplos (Diagramas)
• Injectiva:
f: Y = 2x
X1 ≠ x2 => f(x1) ≠ f(x2)
• Não Injectiva:
g:
Y = x2
X1 ≠ x2 e g(x1) = g(x2)
Objectos diferentes => imagens diferentes
Objectos diferentes e imagens iguais
1.
2.
3.
f
.2
.4
.6
-1.
1.
3.
g
.1
.9
Agostinho Pires: págs.3 de 4
Escola E. B. 2/3 Paulo Quintela
Resumo do Módulo 12 – Funções e Gráficos. CEF
Exemplos (diagramas)
• Sobrejectivas
• Não sobrejectivas
“Todo o elemento de B é imagem
de algum elemento de A”
“Existem elementos em B que não
são imagens de algum de A”
1.
2.
3.
A
f
.2
.4
.6
1.
2.
3.
B
A
f
.2
.4
.6
.-9
B
Inversão de Funções
Inverter uma função f, consiste em encontrar a função g = f -1 que
transforme o contradomínio de f no domínio. A sua expressão obtém-se
resolvendo a equação em ordem à variável independente X.
Domínio
f
Contradomínio
y = 3x − 2
A
y + 2 = 3x
y+2
=x
3
3.
4.
6.
Contradomínio
x+2
y=
3
B
.7
.10
.16
g
Domínio
Nota: no fim devem trocar-se as variáveis: y por x e x por y
Agostinho Pires: págs.4 de 4