FUNÇÃO COMPOSTA, FUNÇÃO INVERSA
FUNÇÃO MODULAR
Profª Ms. Letícia B. Celeste Omodei
E
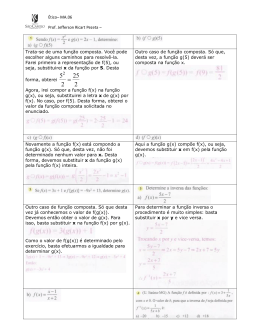
COMPOSIÇÃO DE FUNÇÕES

Dadas as funções f (A em B) e g (C em D), a composição
da função f com a função g é denotada por fog (A em D) e
definida pela expressão
(fog) (x) = f(g(x))
Ex: Dadas as funções f e g (R em R), definidas por
f(x) = x – 5
g(x) = x2 +2x – 3
Calcule:
a) fog (x)
b) fof (x)
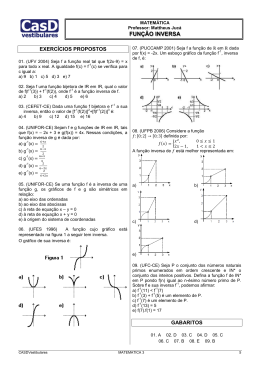
FUNÇÃO INVERSA

Consideremos as funções, f, g e h, definidas
pelos diagramas
FUNÇÃO INVERSA

É possível obtermos funções de B em A, ou de D
em C, ou ainda de F em E, invertendo os sentidos
das flechas?
FUNÇÃO INVERSA
Troca X por Y
 Isola Y


Ex:
FUNÇÃO INVERSA
Não confundir f-1 com 1/f.
Resolver ex 1 p. 24.
MÓDULO (OU VALOR ABSOLUTO) DE UM
NÚMERO
O módulo (ou valor absoluto) de um número real x, que se indica por
| x | é definido da seguinte maneira:
 x, se x  0
x 
 x, se x  0
Então:
 se x é positivo ou zero, | x | é igual ao próprio x.
Exemplos: | 2 | = 2 ; | 1/2 | = | 1/2 | ; | 15 | = 15
 se x é negativo, | x | é igual a -x.
Exemplos: | -2 | = -(-2) = 2 ; | -20 | = -(-20) = 20
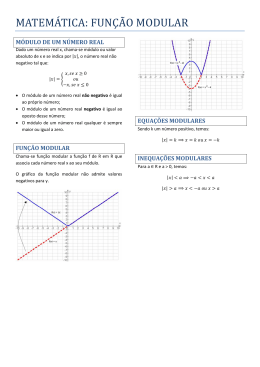
FUNÇÃO MODULAR
Chamamos de função modular a função f(x)=|x| definida por:
 x, se x  0
f ( x)  
 x, se x  0
Observe, então, que a função modular é uma função definida por duas sentenças.
 Determinação do domínio
Vamos determinar o domínio de algumas funções utilizando inequações
modulares:
Exemplo 1: Determinar o domínio da função
1
f ( x) 
| x | 3
Resolução:
1
só é possívelem IR se | x | 3  0.
| x | 3
Então: | x | 3  0  | x | 3  x  3 ou x  3
Sabemos que
Resposta: D  {x  IR | x  3 ou x  3}
Gráfico
Vamos construir o gráfico da função f(x)=|x|:
x
y=f(x)
-1
1
-2
2
0
0
1
1
2
2
Resolver o “para você fazer” da página 30
Gráfico da função f(x)=|x|: