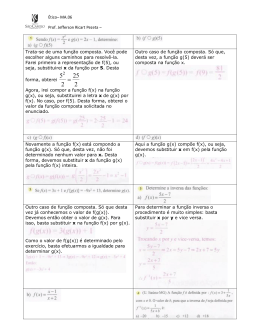
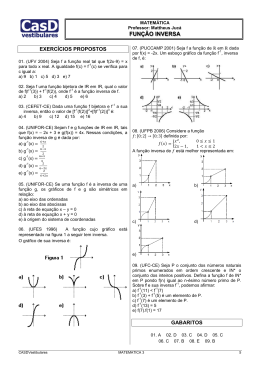
▼
Questão 64
Considere a matriz
A=
a
2a + 1
a–1
a+1
,
em que a é um número real. Sabendo que A admite inversa A –1 cuja primeira coluna é
2a – 1
,
–1
a soma dos elementos da diagonal principal de A –1 é igual a
a) 5
b) 6
c) 7
d) 8
e) 9
Resolução
(
)
2a – 1 x
a inversa de A, temos:
–1
y
a
2a + 1
2a – 1 x
1
A ⋅ A–1 = I2 ∴
⋅
=
a–1 a+1
–1
y
0
Sendo A –1 =
(
)(
) (
0
1
)
Efetuando-se os produtos relativos à primeira coluna, devemos ter:

a ⋅ (2a – 1) – 1 ⋅ (2a + 1) = 1
(a – 1) ⋅ (2a – 1) – 1 ⋅ (a + 1) = 0
(
)
(
)
2 5
3 –5
. Sua inversa é dada por A –1 =
e, portanto,
1 3
–1 2
a soma dos elementos da diagonal principal é 2 + 3 = 5.
Resolvendo o sistema, obtemos a = 2 e, assim, A =
Resposta: a