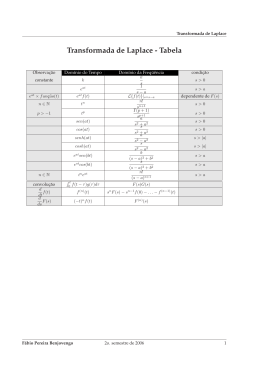
Transformada de Laplace
Prof. André Marcato
Livro Texto: Engenharia de Controle Moderno – Quarta Edição –
Editora Pearson Prentice Hall – Autor: Katsuhiko OGATA
1
Introdução
Funções Comuns
Senoidais
Senoidais Amortecidas
Exponenciais
Operação de Diferenciação
Operação de Integração
Equação Diferencial Linear
Aula 2
£
Funções Algébricas de 1 variável
complexa
2
Introdução

Solucionar Equações Diferenciais Lineares
 Diferenciação e Integração: Operações
Algébricas no Plano Complexo
 Técnicas Gráficas para prever o desempenho
do sistema sem necessidade de solucionar
sistemas de equações diferenciais. Tanto a
componente estacionária quanto a transitória
da solução são obtidas simultaneamente
Aula 2
3
Revisão das Variáveis e Funções
Complexas

Variáveis Complexas

Funções Complexas

Função Complexa Analítica Numa Dada
Região

Aula 2
G(s) e todas as suas derivadas existirem nessa
região
4
Existência da Derivada de Uma
Função Analítica G(s)
Aula 2
5
Exemplo:
Satisfaz as condições de
Cauchy-Riemann para todos
os pontos, exceto s = -1
Aula 2
6
Derivada de G(s) (1)
Aula 2
7
Derivada de G(s) (2)
Aula 2
8
Pólos e Zeros
Aula 2

Pólos: Pontos Singulares em que a função
G(s) ou suas derivadas tendem ao infinito.

Zeros: Pontos nos quais G(s) é nula.

Pontos Ordinários: Pontos do Plano s onde
G(s) é analítica

Pontos Singulares: Pontos do Plano s onde
G(s) não é analítica.
9
Ilustração
Aula 2
10
Teorema de Euler
Aula 2
11
Transformada de Laplace (1)
Aula 2
12
Transformada de Laplace (2)
Aula 2
13
Transformada Inversa de Laplace
Aula 2
14
Função Exponencial
A e α são constantes.
Aula 2
15
Função Degrau
A é uma constante.
Aula 2
16
Função Rampa
A é uma constante.
Aula 2
17
Função Senoidal
A e ω são constantes.
Aula 2
18
Função Cossenoidal
Aula 2
19
Pares de Transformadas de Laplace(1)
Aula 2
20
Pares de Transformadas de Laplace(2)
Aula 2
21
Pares de Transformadas de Laplace(3)
Aula 2
22
Pares de Transformadas de Laplace(4)
Aula 2
23
Função Transladada(1)
Já que:
Temos que:
Aula 2
24
Função Transladada(2)
Aula 2
25
Função Pulso Retangular
Aula 2
26
Função Impulso
A Função Impulso em que a área é igual a unidade é chamada função impulso
unitário ou função delta de Dirac. E a função impulso unitário que ocorre em t =
t0 é normalmente representada por:
Aula 2
27
Multiplicação de f(t) por e-αt
Exemplos:
Aula 2
28
Mudança de Escala de Tempo
Aula 2
29
Exemplo Mudança Escala de Tempo
Alternativamente:
Aula 2
30
Comentários Sobre o Limite Inferior
da Integral de Laplace
Aula 2
31