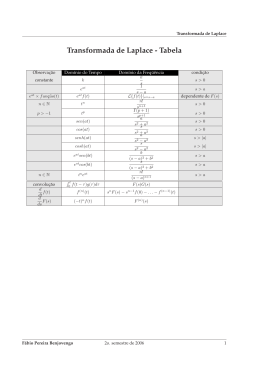
Aula Teórica 3: Função de Transferência
Conteudo
• Definição de Função de Transferência
• Função de Transferência de Sistemas Modelados
Função de Transferência
é o modelo matemático mais usado em controle de sistemas
lineares.
Obs: Na vida real nenhum sistema é totalmente linear
Mas Justifica-se a aproximação se:
• O sistema opera em uma região onde seu comportamento é
linear
• O sistema nao é lineal mas utilizam-se técnicas de linealização
no ponto de operação.
A Função de Transferência é a relação por quociente entre a
saída e a entrada de um sistema, transformadas pelo Laplace
e considerando condições iniciais nulas
saída
Função de
Transferência
Y (s)
G (s) 
U (s)
operador do Laplace
entrada
Nota Importante
Terá que refrescar os conhecimentos de matemática
relacionados com a transformada direta e inversa do Laplace
Suponha
Que pode conhecer as leis físicas que regem as relações entre
as variáveis de um sistema
Que quando utiliza esse conhecimento lhe resulta uma
equação diferencial como a seguinte
Que os coeficientes a e b são constantes
Se toma transformada do Laplace em ambos os membros da
equação e supõe condições iniciais zero como se expõe no
conceito de função de transferência
Então terá
Reorganizando fica
Propriedades importantes da Função de Transferência
• Só está definida para um sistema linear invariante com o tempo.
nunca para sistemas não lineares
• É independente da entrada
• Só se expressa em função da variável complexa S.
nunca em função do tempo ou de outra variável independente
Se tomarmos o seguinte:
O grau do polinômio do numerador m
O grau do polinômio do denominador n
Entao a Função de Transferência diz-se:
• Estritamente Própria n m
• Própria
nm
• Imprópria n m Nenhum sistema físico real cumpre com isto
Funcao de Transferencia de Sistemas Modelados
Circuitos analógicos Elétricos
Por efeitos de estudos de sistemas analogos apresentar-se-a 2 circuitos:
• Circuito RLC-serie
• Circuito RLC-Paralelo
Circuito RLC-Serie
Aplicando a transformada de Laplace teremos:
A funcao de transferencia do sistema sara dada por:
𝐺 𝑠 =
𝑄(𝑠)
1
𝐶
=
=
𝑈(𝑠) 𝐿𝑆 2 + 𝑅𝑆 + 1 𝐿𝐶𝑆 2 + 𝑅𝐶𝑆 + 1
𝐶
Circuitos analógicos Electrónicos
Bloco analogico de Primeira Ordem
As equações do bloco analógico de primeira ordem são dadas abaixo:
Substituindo i, i‘ e i” na primeira dessas equacoes, obtemos:
E aplicando a transformada de Laplace temos:
A função de transferência do sistema sara dada por:
1
𝑅
−
𝑉(𝑠)
𝑅1 𝐶
𝑅1
𝐺 𝑠 =
=
=−
𝑈(𝑠) 𝑆 + 1
𝑅𝐶𝑆 + 1
𝑅𝐶
Bloco analogico de Segunda Ordem
Considerando o caso anterior, relativo ao bloco de primeira ordem, podemos
escrever:
E aplicando a transformada de Laplace temos:
A função de transferência do sistema será dada por:
1
𝑉(𝑠)
𝑅𝑅2 𝐶1 𝐶2
𝐺 𝑠 =
=
1
𝑈(𝑠) 𝑆 2 + 1 𝑆 +
𝑅1 𝐶1
𝑅2 𝑅3 𝐶1 𝐶2
Exercício
• Obtenha a funcao de transferencia dos
seguintes circuitos elétricos