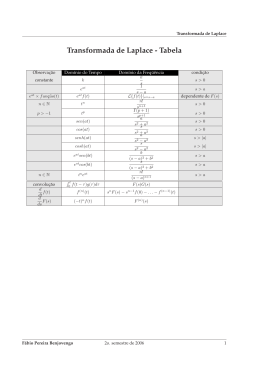
Sinais e Sistemas
UNIDADE 5 – Representação em domínio da frequência para sinais contínuos:
Transformada de Laplace
Lista de Exercícios 01
Entrega: 16/11/2011 (quarta-feira), até as 15h00
1) Usando a definição de Transformada de Laplace (integral de Laplace), encontrar a Transformada
de Laplace de:
0 , para t  0
.
f  t    3t
te , para t  0
Resp.: F  s  
1
 s  3
2
.
2) Determinar a Transformada de Laplace da seguinte função (pode-se empregar a tabela de pares
de transformada):
, para t  0
0
.
f t   
 sen  ωt  θ  , para t  0
Onde θ é uma constante.
Resp.: F  s  
ω cos  θ   s sen  θ 
.
s 2  ω2
3) Determinar a Transformada de Laplace da função f(t) representada na figura abaixo. Encontrar também
o valor-limite de F(s) quando a tende a zero. Dica: escrever f(t) como a soma de funções degrau.
Resp.: F  s  
1
1  2e  as  e2 as  e lim F  s   s .
2 
a 0
a s
4) Determinar a Transformada Inversa de Laplace da seguinte função (pode-se empregar a tabela de
pares de transformada):
F s 
1
.
s  s  2s  2 
2
Resp.: f  t  
1 1 t
1
 e sen  t   e t cos  t  , para t  0 .
2 2
2
5) Determinar a Transformada Inversa de Laplace da seguinte função (pode-se empregar a tabela de
pares de transformada):
F s 
5  s  2
.
s  s  1 s  3
2
Resp.: f  t   
25 10 5  t 5 3t
 t  e  e , para t  0 .
9 3
2
18
6) Obtenha a solução da seguinte equação diferencial através do emprego da Transformada de Laplace:

x  3 x  6 x  0, x  0   0, x  0   3 .
Resp.: x  t  
 15 
2 3 1,5t
e sen 
t  .
2
5

