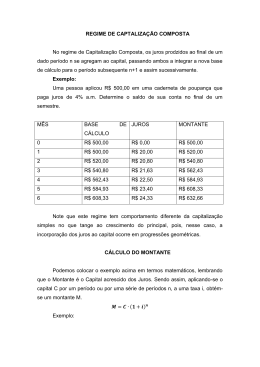
PROF. ANTÔNIO CERQUEIRA
SUM ÁRIO
CAPÍTULO I – CONSIDERAÇÕES GERAIS
II.1 – Fundamentos Teóricos
II.2 – Equivalência do Valor do Dinheiro no Tempo
II.3 – A Análise Econômica
II.4 – O Processo de Tomada de Decisão
II.5 – Aplicação Prática
CAPÍTULO II - MATEM ÁTICA FINANCEIRA
II.1 – Juros
II.2 – Taxa de Juros
II.3 – Diagrama do Fluxo de Caixa
II.4 – Regras Básicas
II.5 – Regime de Capitalização de Juros
II.6 – Aplicações Práticas dos Juros Simples e Compostos
II.7 – Capitalização Contínua e Descontínua
II.8 – Fórmula de Juros Simples
II.9 – Montante e Capital
II.10 – Taxa Equivalente e Taxa Proporcional
II.11 – Juros Exatos e Juros Comerciais
II.12 – Equivalência Financeira
II.13 – Exercícios Resolvidos
II.14 – Exercícios Propostos
II.15 – Respostas dos Exercícios Propostos de Juros Simples
II.16 – Juros Compostos
II.17 – Fórmulas de Juros Compostos
II.18 – Taxas Equivalentes
II.19 – Exercícios Propostos
II.20 – Respostas dos Exercícios Propostos de Juros Compostos
CAPÍTULO III - ANÁLISE DE ALTERNATIVAS DE INVESTIMENTOS
III.1 - Generalidades
III.2 - Taxa Mínima de Atratividade
III.3 - Critérios Econômicos de Decisão
III.4 - Circunstâncias Específicas
III.5 - Problemas Propostos
CAPÍTULO IV – DEPRECIAÇ ÃO DO ATIVO IMOBILIZADO
IV.1 – O Ativo Imobilizado
IV.2 – Métodos de Depreciação
CAPÍTULO V - FINANCIAMENTOS
VI.1 - Amortização de Dívidas
VI.2 - Exercícios Propostos
CAPÍTULO VI - ANÁLISE DE SENSIBILIDADE
CAPÍTULO VII - ANÁLISE DA VIABILIDADE ECONÔMICA DE UM PROJETO INDUSTRIAL
BIBLIOGRAFIA
2
CAPÍTULO I
CONSIDERAÇÕES GERAIS
3
I.1 – HISTÓRICO
Os estudos sobre engenharia econômica têm suas origens nos Estados Unidos, em 1887,
quando Arthur Wellington publicou seu livro The Economic Theory of Railway Location, texto que
sintetizava análise de viabilidade econômica para ferrovias. Wellington, que era engenheiro civil,
ponderava que devia utilizar-se o método de análise de custo capitalizado para selecionar o traçado e
as curvaturas das vias férreas.
Na década de 20, J. C. L. Fish e 0. B. Coldman estabeleceram algumas metodologias de
análise de investimento em estruturas de engenharia sob a perspectiva da matemática atuarial.
Coldman, no livro titulado Financial Engineering, propôs um método analítico baseado em juros
compostos para determinar valores comparativos. Os limites da clássica engenharia econômica foram
traçados, em 1930, por Eugene L. Grant, no livro Principles of Engineering Economy, onde são
estabelecidos os tradicionais critérios de comparação e de avaliação de investimentos.
Antes da segunda guerra mundial, os bancos e bolsas de valores dos paises eram as únicas
instituições que utilizavam termos como juros, capitalização, amortização. A partir dos anos 50, com o
rápido crescimento industrial, termos financeiros e bancários passam a ser incorporados no âmbito
industrial e particularmente na área produtiva das empresas. Os novos industriais se depararam com
a necessidade da aplicação de técnicas de análise econômica em suas empresas, criando um
ambiente de tomada de decisões voltado à escolha da melhor alternativa.
À medida que o processo industrial se tornava mais complexo, as técnicas se adaptaram e se
tornaram mais especificas, para tanto, a engenharia econômica ou a análise econômica na
engenharia foi também se evoluindo. Pesquisas modernas, refletindo a preocupação mundial pela
conservação dos recursos e da aplicação eficaz de dinheiro público, ampliaram as fronteiras da
engenharia econômica, incorporando aos métodos de avaliação tradicionais, novos critérios para a
avaliação do risco, da sensibilidade, de fatores intangíveis etc.
Ao longo de 120 anos, a engenharia econômica foi sendo aprimorada e aplicada em
inúmeras outras áreas além da engenharia, contudo, esta terminologia foi conservada pelo fato de
que grande parte dos problemas de alocação de recursos depende de informações técnicas e em
geral de decisões, que são tomadas por engenheiros ou por administradores, que agem com base
nos fundamentos da engenharia.
I.2 – DEFINIÇÃO E PRNCÍPIOS BÁSICOS
A engenharia econômica é definida como a aplicação da análise e síntese econômica ou
matemática às decisões de engenharia ou um corpo de conhecimentos e técnicas envolvidas na
avaliação do valor de mercadorias e serviços relativamente ao custo e nos métodos de estimar os
dados. É importante para todos que precisam decidir sobre propostas tecnicamente corretas. Seus
fundamentos podem ser utilizados tanto para empresas privadas como estatais. Todo o fundamento
da engenharia econômica se baseia na matemática financeira, que se preocupa com o valor do
dinheiro no tempo.
Podem-se citar como exemplos de aplicação:
transporte de materiais manualmente ou por meio de correia transportadora;
substituição de equipamentos obsoletos;
comprar veículo a prazo ou à vista;
realizar serviços diretamente ou terceirizá-los.
Para fazer um estudo econômico adequado alguns princípios básicos devem ser
considerados, sendo os seguintes:
a) alternativas de investimentos. É infrutífero calcular se é vantajoso comprar um carro à vista
se não há condições de conseguir dinheiro para tal;
4
b) alternativas expressas em valores monetários. Não é possível comparar 300 horas
mensais de mão de obra com 500 kwh de energia. Convertendo os dados em termos monetários,
tem-se um denominador comum muito prático. Entretanto, alguns dados são difíceis de serem
expressos em valores monetários. Exemplos: boa vontade de um fornecedor, imagem da empresa no
mercado. São os chamados intangíveis;
c) apenas as diferenças são relevantes. Numa análise para decidir sobre o tipo de motor a
comprar, não interessa se o consumo de energia dos mesmos for igual;
d) juros sobre o capital empregado. Sempre existem oportunidades de emprego de dinheiro
em outras atividades, quer sejam produtivas quer sejam especulativas. Ao se aplicar um capital em
um projeto devemos ter certeza de ser esta a maneira mais rentável de utilizá-lo;
e) nos estudos econômicos, o passado geralmente não é considerado; interessa-nos o
presente e o futuro. A afirmação: não posso vender este carro por menos de R$ 10.000,00, porque
gastei isto com ele em oficina, não faz sentido. O que normalmente interessa é o valor de mercado do
carro.
Os critérios de aprovação de um projeto são os seguintes:
• critérios financeiros: disponibilidade de recursos;
• critérios econômicos: rentabilidade do investimento;
• critérios imponderáveis: fatores não convertidos em dinheiro.
Nos problemas de engenharia econômica considera-se que todos os pagamentos ou séries
de pagamentos futuros que reembolsem uma quantia presente com juros são equivalentes entre si.
É, assim, possível comparar alternativas de investimento com diferentes séries prospectivas de
receitas e despesas utilizando os métodos do valor anual equivalente, valor presente, taxa de
rendimento e/ou análise benefício-custo. Estes métodos, quando utilizados correctamente, permitem
chegar a conclusões idênticas.
I.3 – FUNDAMENTOS TEÓRICOS
Os fundamentos da engenharia econômica são um conjunto de princípios ou conceitos que
formam uma base sólida para o desenvolvimento, estudo e aplicação da disciplina. São eles:
1. reconhecer e definir alternativas. As decisões são entre alternativas; é desejável que as
alternativas sejam definidas claramente e que os méritos de todas as alternativas
apropriadas sejam avaliados;
2. a necessidade de considerar as consequências. As decisões devem ser baseadas nas
consequências esperadas das várias alternativas. Todas essas consequências ocorrerão
no futuro;
3. a questão crítica das consequências para quem. Antes de estabelecer procedimentos
para formulação de projetos e avaliação de projetos, é essencial decidir qual o ponto de
vista a ser adaptado;
4. comensurabilidade. Ao comparar alternativas, é desejável fazer as consequências
comensuráveis entre si, tanto quanto seja praticável. Isto é, as consequências de um
investimento devem ser expressas em números e as mesmas unidades devem aplicar-se
a todos os números. Em decisões económicas, as unidades monetárias são as únicas que
satisfazem as especificações dadas acima;
5. irrelevância de aspectos comuns a todas as alternativas. Só as diferenças entre
alternativas são relevantes na sua comparação;
6. separação das decisões. Na medida do possível, decisões separáveis devem ser feitas
separadamente;
5
7. necessidade de critérios de decisão. É desejável ter um critério para a tomada de
decisão ou possivelmente vários critérios;
8. escolha do critério principal. O critério principal a ser aplicado numa escolha entre
investimentos propostos alternativos em bens corpóreos deve ser selecionado com o
objetivo de fazer o melhor uso de recursos limitados;
9. critérios secundários aplicados às consequências expressas em termos monetários.
Até mesmo as estimativas mais cuidadosas das consequências monetárias da escolha de
alternativas diferentes podem revelar-se incorrectas. É muitas vezes útil, a um decisor,
fazer uso de critérios secundários que reflectem, de alguma forma, a falta de certeza
associada a todas as estimativas do futuro;
10. dados irredutíveis do problema do investimento. As decisões entre alternativas de
investimento devem dar peso a quaisquer diferenças esperadas nas consequências que
não tenham sido reduzidas a termos monetários, assim como nas consequências que
tenham sido expressas em termos monetários;
11. a necessidade de um ponto de vista sistêmico. Muitas vezes, há efeitos secundários
que tendem a ser menosprezados quando são tomadas decisões individuais. Para
considerar esses efeitos secundários, adequadamente, pode ser necessário examinar as
inter-relações entre um número de decisões, antes de poder ser tomada qualquer das
decisões individuais.
Os outros dois princípios, sugeridos por DeGarmo et al., são:
tornar explícito o risco e/ou incerteza. O risco e/ou incerteza são inerentes à projeção
(ou estimativa) de valores futuros e devem ser reconhecidos na análise e comparação
das alternativas;
avaliar as decisões. A melhoria na tomada de decisões resulta de um processo
adaptativo; na medida do possível, os valores inicialmente previstos para a alternativa
selecionada e os resultados realmente alcançados devem ser comparados,
subsequentemente.
I.4 – EQUIVALÊNCIA DO VALOR DO DINHEIRO NO TEMPO
Em estudos, seja para fins de avaliações econômicas ou avaliações financeiras de
empreendimentos, seja para a análise de resultados ou indicadores históricos de investimentos, é
comum se lidar com valores financeiros relacionados a épocas ou períodos diferentes. A capacidade
que o dinheiro tem de gerar rendimento com o transcurso do tempo faz com que um mesma cifra, em
valor nominal, tenha diferentes valores em relação ao tempo a que se refere o que realmente
descreve o conceito do Valor do Dinheiro no Tempo. O dinheiro, como qualquer outro bem, tem um
valor intrínseco e seu valor sofre variação em função da variação (maior/menor) da oportunidade
(compra/rendimento) gerada em função do tempo.
Uma pessoa pode possuir uma casa ou trocar este bem por dinheiro ou possuir um veículo
ou vendê-lo para, em troca, receber o valor em dinheiro. Por outro lado, se a pessoa não possui uma
casa e necessita de uma, é obrigada a recorrer ao aluguel, pagando por este uso. Se não possui um
automóvel e necessita de um, deve pagar por esta locação, não importando se é por meia hora, como
no caso de táxi, ou por um dia ou um mês. Do mesmo modo, se alguém não possui dinheiro e
necessita dele, deve pagar certa quantidade para obtê-lo. Em geral, todo bem com valor intrínseco
exige um pagamento pelo seu uso. Por outro lado, se bens com valores intrínsecos não são
utilizados, nada se ganha com eles, seria o mesmo que ter um táxi na garagem ou guardar dinheiro
sob o colchão.
A capacidade de valorização do dinheiro com o tempo só existe quando em plena atividade, é
o caso de uma operação de empréstimo: quem recebe dinheiro de empréstimo paga ao final de um
6
determinado prazo uma quantidade de dinheiro maior que o valor emprestado. O incremento que é
pago ao dono do dinheiro é chamado de juros e traduz o conceito de Valor do Dinheiro no Tempo.
O conceito de Valor do Dinheiro no Tempo muitas vezes e isoladamente exemplificado por
meio do fenômeno inflacionário, embora o que realmente ocorre nesta situação é o fenômeno da
“ilusão monetária”, efeito tanto maior quanto maior o país padece da inflação.
A inflação é um fenômeno econômico que consiste na perda de poder aquisitivo do dinheiro
com o passar do tempo, em decorrência da elevação do nível geral de preço no mercado interno.
Portanto, o dinheiro se desvaloriza com a inflação. Nenhum país está imune ao fenômeno da inflação,
diz-se que este valor é baixo quando se encontra entre 2 a 5 % ao ano, como ocorre nos paises
desenvolvidos, porém, chega a atingir patamares acima de 1.000% anuais, como vivenciados pelo
Brasil na década de 90. A Tabela 1 mostra a variação inflacionária no Brasil desde 1980 até os dias
atuais.
Tabela 1
Inflação anual no Brasil – Variação do IGP-DI (Índice Geral de Preços - Disponibilidade Interna)
ANO
1980
1981
1982
1983
1984
1985
1986
1987
1988
1989
1990
INFLAÇÃO (%)
110,25
95,20
99,71
210,98
223,81
235,13
65,04
415,87
1.037,53
1.782,85
1.476,71
ANO
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
INFLAÇÃO (%)
480,17
1.157,84
2.708,39
909,67
14,77
9,33
7,48
1,71
19,99
9,80
10,40
ANO
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
INFLAÇÃO (%)
26,41
7,67
12,13
1,22
3,79
7,89
9,10
- 1,43
11,30
5,01
8,11
Fonte: Fundação Getúlio Vargas (FGV)
Vale ressaltar que independente da inflação, o dinheiro pode se valorizar através do tempo,
caso a remuneração cobrada pelo uso do dinheiro seja menor que a perda de seu valor aquisitivo em
decorrência da inflação. Significa que a perda total do investidor inclui a diferença entre a
remuneração recebida e a desvalorização do dinheiro, mais a valorização real pretendida na
operação de empréstimo. Com técnicas analíticas adequadas se pode comparar o poder aquisitivo do
dinheiro em determinados instantes de tempo, esta é a ajuda que a Engenharia Econômica fornece
aos administradores de negócios.
I.5 – A ANÁLISE ECONÔMICA
Que tipo de problema pode ser resolvido na engenharia econômica?
1. Suficientemente importante, justificando um estudo e esforços sérios;
2. não pode ser resolvido de forma simplória, isto é, exige uma análise cuidadosa, de forma
que seja organizado e que sejam estudadas as consequências;
3. têm aspectos econômicos suficientemente importantes, que constituem um componente
significativo da análise com vistas à tomada de decisão.
Quando o problema apresenta essas três características, a engenharia econômica é uma
técnica apropriada na busca de uma solução.
7
I.6 – O PROCESSO DE TOMADA DE DECISÃO
A tomada racional de decisão é um processo complexo, que envolve vários elementos
essenciais, tais como:
a) reconhecimento de um problema – é o ponto de partida de qualquer tentiva consciente
de tomar uma decisão racional. Somente após o reconhecimento do problema poderemos, de
maneira lógica, iniciar o processo para a sua resolução. Exemplos: peixeis com acetuadas
concentrações de mercúrio; um aciente de automóvel; um cheque sem cobertura; um motor
queimado; um estoque de peças esgotado;
b) definição do objetivo – todo problema é uma situação que nos impede de atingirmos
objetivos previamente determinados. Exemplos: lucro de uma empresa; saldar o empréstimo da
compra de um carro; aumentar a produção no próximo mês. A definição de um objetivo é o ato de
descrevê-lo exatamente;
c) coleta de dados relevantes – para tomar-se um decisão, é fundamental a qualidade da
informação a respeito. Exemplos: existem informações publicadas. Todavia, há enorme quantidade
de informação não escrita em lugar algum (experiências pessoais). Ainda há informações que
permanecem não coletadas; quantas pessoas estariam interessadas em comprar um par de tesouras
para canhoto? Seria necessária uma pesquisa de mercado ou outro tipo de coleta de dados para
ober-se a informação desejada. Uma fonte importante de dados costuma ser o conjunto de registros
contábeis da própria companhia, especialmente os custos e os benefícios.
Algumas das formas mais fácieis de decisão em engeharia se relacionam com problemas de
projetos, métoddos ou materiais alternados. Coomo os resultaados ocorrem dentro de um prazo
bastante curto, podemos rapidamente adicionar os custos e benefícios de cada alterntiva. Então,
adotando o critério econômico adequado, pode-se identificar a melhor alternativa.
I.7 – APLICAÇÃO PRÁTICA
1. Os registros contábeis de uma grande companhia acusam os seguintes custos médios
mensais do seu departamento de impressão, constituído de três funcionários:
Elemento de Despesa
Mão de obra direta e salários
Material e suprimentos consumidos
2
2
Alocação de custos gerais indiretos (200 m de área a R$ 25,00/m )
Soma
Valor (R$)
6.000,00
7.000,00
5.000,00
18.000,00
O departamento de impressa debita seus serviços aos outros departamentos, a fim de
recuperar seu custo mensal de R$ 18.000,00. Por exemplo, para imprimir 1.000 cópias de um
anúncio, o débito é:
Elemento de Despesa
Mão de obra direta e salários
Material e suprimentos consumidos
2
2
Alocação de custos gerais indiretos (200 m de área a R$ 25,00/m )
Soma
Valor (R$)
7,60
9,80
9,05
26,45
O departamento de expedição consulta uma gráfica comercial e verifica que pode obter as
1.000 cópias impressas por R$ 22,95. Embora o departamento de expedição necessite de apenas
30.000 cópias por mês, resolve dispensar o serviço do departamento de impressão e imprimir as
cópias na gráfica externa. O departamento de impressão objeta. Como reusltado, o gerente geral
determiina que um funionário estude a situação e recomende o que deve ser feito.
Solução:
8
Componente
Mão de obra direta e salários
Material e suprimentos
2
2
Custos gerais indiretos (200 m a 25,00/m )
Soma (R$)
Departamento de Impressão
1.000 cópias
30.000 cópias
7,60
228,00
9,80
294,00
9,05
271,50
26,45
793,50
Gráfica Externa
1.000 cópias 30.000 cópias
22,95
688,50
Utilizando os serviços da gráfica externa, o departamento de expedição reduziria seu custo
de R$ 793,50 para R$ 688,50. Nesse caso, de quanto seria a redução dos custos do departamento
de impressão? Examinaremos cada um dos componentes de custo:
. mão de obra direta – R$ 228,00 – não há redução;
. materiais e suprimentos – haveria uma economia de R$ 294,00;
. custos gerias indiretos – não haverá qualquer redução na quota mensal de R$ 5.000,00 do
departamentos de impressão, pois não haverá redução do espaço físico.
A companhia economizará R$ 294,00 em materias e suprimentos e pode, ou não, economizar
R$ 228,00 em mão de obra se o departamento de impressão deixar de trabalhar com o departamento
de expedição. A economia máxima seria de 294,00 + R$ 228,00 = R$ 522,00. Mas se o departamento
de expedição for autorizado a contratar seu trabalho de impressão com uma gráfica externa, a
companhia deverá arcar com uma despesa mensal de R$ 688,50. A economia decorrente do
departamento de impressão em não fazer o trabalho para o departamento de expedição não
excederia a R$ 522,00, e, provavelmente, seria de apenas R$ 294,00. O resultado seria um aumento
de custo para companhia.
Por esta razão, o departamento de expedição deve ser aconcelhado a não contratar os
serviços de uma gráfica externa. Vale ressalrtar que cópias externas levam ao conhecimento de
pessoas estranhas, documentos sigilosos da companhia.
2. Um agregado de concreto deve conter ao menos 31% de areia por volume para uma
composição adequada. Um tipo de material, que apresenta 25% de areia e 75% de agregado bruto, é
3
vendido a R$ 3,00/m . Outro tipo, que tem 40% de areia e 60% de agregado, é vendido a R$ 4,40 o
metro cúbico.
Determinar o custo mínimo, por metro cúbico, da amostra dos dois agregados.
Solução:
O custo mínimo da nistura dis dius agregados resulta da utilização máxima do materual de
custo mais baixo. O material de custo mais elevado será usado para aumentar a proporção de ateria
até o nível mínimo (31%) especificado.
Seja X = parcela de agregado da fonte de R$ 3,00/ m
3
1 – X = parcela de agregado da fonte de R$ 4,40/ m
3
Quantidade de areia:
X (0,25) + (1 –X) (0,40) = 0,31
0,25 X + 0,40 – 0,40 X = 0,31
0,25 X – 0,40 X = 0,31 – 0,40
– 0,15 X = – 0,09
X = – 0,09/– 0,15 = 0,60 ↔ 60%
Assim, os agregados misturados conterão:
3
3
60% de material de R$ 3,00/m = R$ 1,80 m
3
3
40% de material de R$ 4,40/m = R$ 1,76 m
9
3
Portanto, o custo mínimo da mistura dos dois agregados será R$ 3,56 m .
3. Uma peça de máquina pode ser fabricada ao custo unitário de R$ 0,40 de material e R$
0,15 de mão de obra direta, exigindo um investimento de R$ 500.000,00 em maquinaria. Um pedido
compreende três milhões de peças. A meio caminho da execução do pedido, pode-se introduzir um
novo processo de fabricação que reduz os custos unitários para R$ 0,34 de material e R$ 0,10 de
mão de obra direta – mais exigiria um equipamento adicional que custa R$ 100.000,00. Os custos
indiretos equivalem a 2,5 o custo da mão de obra, em média. Pergunta-se: deve-se continuar a
produção da peça pela alternativa A (continuar com o processo em vigor) ou passar para alternativa B
(mudar o processo de fabricação)?
Solução:
Custo
Maquinaria adicional
Material
Mão de obra direta
Outros custos
Para 1.500.000 peças
Alternativa A (R$)
1.500.000 peças x 0,40 = 600.000,00
1.500.000 peças x 0,15 = 225.000,00
2,5 x 225.000 = 562.500,00
1.387.500,00
Alternativa B (R$)
100.000,00
1.500.000 peças x 0,34 = 510.000,00
1.500.000 peças x 0,10 = 150.000,00
2,5 x 150.000 = 375.000,00
1.135.000,00
Antes de tomar uma decisão, devemos examinar devidamente os outros custos, para ver se
eles, de fato, variam quando o custo da mão de obra varia. Supondo que isso ocorra, a decisão será
mudar o processo de fabricação.
4. No planejamento de um armazém frigorífico, as especificações exigem uma transferência
2
máxima de calor, através das paredes do armazém, de 30.000 joules/h/m de parede, quando há uma
diferença de temperatura de 30 °C entre a superfície interna e a superfície externa de isolamento. Os
dois materiais isolantes em estudo são:
Material Isolante
Lã mineral
Espuma isolante
2
Custo por m (R$)
12,50
14,00
2
Condutividade (j-m/m °c– h)
140
110
A equação básica da condução do calor através de uma parede é:
Q = k (∆t)
L
Onde:
2
Q = transferência de calor em j/h/m de parede;
2
K = condutividade em j-m/m -°c-h;
∆T = diferença de temperatura entre duas superfícies, em °C;
L = espessura do material isolante, em metros.
Qual material isolante deve ser escolhido?
Solução:
A resolução do problema comporta dois passos. Primeiro deve-se calcular a espessura
exigida de cada um dos materiais. Em seguida, como o problema é uma questão de benefício fixado
(a transferência de calor através da parede é limitada a uma quantidade fixa máxima), o critério
consiste em minimizar a utilização de insumo (minimizar o custo).
Material Isolante
Lã mineral
Espuma isolante
Espessura (m)
140 (30) / 30.000 = 0,14
110 (30) / 30.000 = 0,11
Custo do isolamento (R$)
3
2
12,50 m x 0,14 m = 1,75 m
3
2
14,00 m x 0,11 m = 1,54 m
Portanto, a espuma isolante é a alternativa mais barata.
10
CAPÍTULO II
MATEMÁTICA FINANCEIRA
11
A matemática financeira trata, em essência, do estudo do valor do dinheiro ao longo do
tempo. O seu objetivo básico é o de efetuar análises e comparações dos vários fluxos de entrada e
saída de dinheiro de caixa, verificados em diferentes momentos. E pode-se iniciar o estudo sobre o
tema com a seguinte frase:
“NÃO SE SOMAM OU SUBTRAEM QUANTIAS, EM DINHEIRO, QUE NÃO ESTEJAM NA MESMA DATA”.
Embora esta afirmativa seja básica e simples, é absolutamente incrível como a maioria das
pessoas esquece ou ignoram esta premissa.
Uma palavra que é fundamental nos estudos sobre matemática financeira é juro. Cada um
dos fatores de produção é remunerado de alguma forma. Como se podem entender, então, os juros
são o que se paga pelo custo do capital, ou seja, o pagamento pela oportunidade de poder dispor de
um capital durante determinado tempo.
FIGURA 1 – FATORES ECONÔMICOS DE PRODUÇÃO
A propósito estamos muito acostumados com "juros", lembrem-se dos seguintes casos:
1. compras a crédito;
2. cheques especiais;
3. prestação da casa própria;
4. desconto de duplicata;
5. Vendas a prazo;
6. Financiamentos de automóveis;
7. Empréstimos.
Como se pode ver o termo é muito familiar se lembrarmos do nosso dia a dia. Podemos até
não nos importar com a questão, mas a pergunta que se faz é o quanto pagamos por não
considerarmos adequadamente a questão? E concluindo, nota-se a correspondência entre os termos
"juros" e "tempo", que estão intimamente associados.
A seguir será discutido o que são juros simples e juros compostos, além de outros pontos
importantes em matemática financeira.
12
II.1 – JUROS
Refere-se à remuneração de um valor (capital), que incide sobre o mesmo.
II.2 – TAXAS DE JUROS
As taxas de juros devem remunerar:
a) o risco envolvido na operação;
b) a perda do poder de compra (aquisitivo) motivada pela inflação;
c) o capital emprestado/aplicado.
As taxas de juros se referem sempre a uma unidade de tempo: mês, semestre, ano etc.
Podem ser representadas por taxa percentual e taxa unitária.
a) Taxa Percentual – refere-se aos “contos” do capital, ou seja, o valor dos juros para cada
centésima parte do capital.
Ex.: um capital de R$ 1.000,00, aplicado a uma taxa de 20% ao mês, renderá quando de
juros, ao final deste período?
juros = R$ 1.000,00 x 20
100
juros = R$ 10,00 x 20 = R$ 200,00
O capital de R$ 1.000,00 tem dez centos. Como cada um deles rende 20, a remuneração
total da aplicação no período é, portanto, de R$ 200,00.
b) Taxa Unitária – centra-se na unidade de capital. Reflete o rendimento de cada unidade de
capital em certo período de tempo.
Ex.: no exemplo anterior, a taxa percentual de 20% ao ano indica um rendimento de 0,20
(20/100) por unidade de capital aplicada, ou seja:
Juros = R$ 1.000,00 x 20
100
Juros = R$ 1.000,00 x 0,20 = R$ 200,00.
Taxa Percentual (%)
Taxa Unitária
1,50
0,015
8,00
0,08
17,00
0,17
86,00
0,86
120,00
1,20
1.500,00
15,00
Na matemática financeira, todos os cálculos são efetuados utilizando-se a taxa unitária de
juros. Todavia, os resultados sempre são representados pela taxa percentual.
II.3 – DIAGRAM A DO FLUXO DE CAIXA
Permite que se visualize no tempo, o que ocorre com o capital.
13
Ex.:
+
+
+
+
saída de caixa (-)
(tempo)
0
1
2
3
4
5
6
7
8
A linha horizontal registra a escala do tempo, ou seja, o horizonte financeiro da operação. O
ponto zero indica o momento inicial, e os demais pontos representam os períodos de tempo (datas).
As setas acima da linha do tempo refletem as entradas (recebimentos) de dinheiro, e as setas para
baixo da linha indicam saídas (ou aplicações) de dinheiro.
II.4 – REGRAS BÁSICAS
Nas fórmulas de matemática financeira, tanto a taxa de juros como o período de capitalização
devem estar na mesma unidade de tempo.
Ex.: juros de 2% ao mês e rendimentos creditados mensalmente.
Se a aplicação foi efetuada pelo prazo de um mês, mas os juros definidos em taxa anual, não
há coincidência nos prazos. Nesse caso é preciso que haja uma transformação de uma variável para
a unidade da outra.
II.5 – REGIME DE CAPITALIZAÇÃO DE JUROS
Simples = linear;
Composto = exponencial.
Regime Simples – comporta-se como se fosse uma progressão aritmética (PA), crescendo
os juros de forma linear ao longo do tempo.
Ex.: empréstimo de R$ 1.000,00, pelo prazo de cinco anos, pagando-se juros simples, à
razão de 10% ao ano.
(R$)
Ano
Saldo
Inicial
Juros
Saldo Devedor
Crescimento Anual do
Saldo Devedor
Início 1°
-
-
1.000,00
-
Fim 1°
Fim 2°
1.000,00
0,10 x R$ 1.000,00 = R$ 100,00
1.100,00
100,00
1.100,00
0,10 x R$ 1.000,00 = R$ 100,00
1.200,00
100,00
Fim 3°
1.200,00
0,10 x R$ 1.000,00 = R$ 100,00
1.300,00
100,00
Fim 4°
1.300,00
0,10 x R$ 1.000,00 = R$ 100,00
1.400,00
100,00
Fim 5°
1.400,00
0,10 x R$ 1.000,00 = R$ 100,00
1.500,00
100,00
Regime Composto – equivale a uma progressão geométrica (PG), no qual os juros incidem
sempre sobre o saldo apurado no início do período correspondente (e não unicamente sobre o capital
inicial).
Ex.: admitindo-se no exemplo anterior a dívida de R$ 1.000,00, pelo prazo de cinco anos,
pagando-se juros compostos, à taxa de 10% ao ano, temos:
14
(R$)
Saldo Devedor ao Final de Cada Ano
Ano
Saldo Inicial
Juros
Início 1°
-
-
1.000,00
Fim 1°
1.000,00
0,10 x R$ 1.000,00 = R$ 100,00
1.100,00
Fim 2°
1.100,00
0,10 x R$ 1.100,00 = R$ 110,00
1.210,00
Fim 3°
1.210,00
0,10 x R$ 1.210,00 = R$ 121,00
1.331,00
Fim 4°
1.331,00
0,10 x R$ 1.331,00 = R$ 133,10
1.464,10
Fim 5°
1.464,00
0,10 x R$ 1.464,10 = R$ 146,41
1.610,51
Diante dos resultados obtidos, pode-se elaborar um quadro comparativo dos regimes de capitalização
apresentados:
(R$)
Diferença: composta-simples
Capitalização Simples
Capitalização Composta
Ano
Juros
anuais
Saldo
devedor
Juros
anuais
Início 1°
-
1.000,00
-
1.000,00
-
-
Fim 1°
100,00
1.100,00
100,00
1.100,00
-
-
Fim 2°
100,00
1.200,00
110,00
1.210,00
10,00
10,00
Fim 3°
100,00
1.300,00
121,00
1.331,00
21,00
31,00
Fim 4°
100,00
1.400,00
133,10
1.464,10
33,10
64,10
Fim 5°
100,00
1.500,00
146,41
1.610,51
46,41
110,51
Saldo devedor Juros anuais
Saldo devedor
Representação Gráfica:
R$
capitalização composta
(exponencial)
capitalização simples
(linear)
150
140
130
120
110
0
1
2
3
4
5
Tempo (ano)
II.6 – APLICAÇÕES PRÁTICAS DOS JUROS SIMPLES E COMPOSTOS
Os juros simples têm aplicações práticas bastante limitadas. São raras as operações
financeiras e comerciais segundo o regime de capitalização linear. O juros simples restringem-se
principalmente às operações praticadas no âmbito do curto prazo.
Tecnicamente mais correto por envolver a capitalização exponencial dos juros, o regime
composto é reconhecidamente adotado por todo o mercado financeiro e de capitais.
15
II.7 – CAPITALIZAÇÃO CONTÍNUA E DESCONTÍNUA
Capitalização Contínua – se processa em intervalos de tempo bastante reduzidos. Pode ser
estendida em todo fluxo monetário distribuído ao longo do tempo e não somente num único instante.
Esse regime é pouco utilizado.
Ex.: faturamento de um supermercado; depreciação de um equipamento etc.
Capitalização Descontínua – os juros são formados somente ao final de cada período de
capitalização. Esse regime é bastante generalizado.
Ex.: caderneta de poupança.
II.8 – FÓRMULA DE JUROS SIMPLES
J=c.i.n
j = juros expressos em unidades monetárias (R$);
c = capital, expresso em unidades monetárias (R$);
i = taxa de juros, expressa em forma percentual;
n = prazo.
Exemplo 1.
Um capital de R$ 80.000,00 é aplicado à taxa de 2,5% ao mês, durante um trimestre. Pedese determinar o valor dos juros acumulados neste período.
Solução:
c = R$ 80.000,00
i = 2,5% ao mês = 0,025
n = 3 meses
j=?
J=c.i.n
J = 80.000 . 0,025 . 3
J = R$ 6.000,00
Exemplo 2.
Um negociante tomou um empréstimo, pagando uma taxa de juros de 6% ao mês, durante 9
meses. Ao final deste período, calculou em R$ 270.000,00 o total dos juros incorridos na operação.
Determinar o valor do empréstimo.
Solução:
i = 6% ao mês = 0,06
n = 9 meses
j = R$ 270.000,00
c=?
J=c.i.n
270.000 = c . 0,06 . 9
0,54 c = 270.000
c = 270.000 / 0,54
c = R$ 500.000,00
16
Exemplo 3.
Um capital de R$ 40.000,00 foi aplicado num fundo de poupança por 11 meses, produzindo
um rendimento financeiro de R$ 9.680,00. Pede-se apurar a taxa de juros oferecida por esta
operação.
Solução:
c = R$ 40.000,00
n = 11 meses
j = R$ 9.680,00
i=?
J=c.i.n
9.680 = 40.000 . i . 11
9.680 = 440.000 i
i = 9.680 / 440.000
i = 0,022 = 2,2% ao mês.
Exemplo 4.
Uma aplicação de R$ 250.000,00, rendendo uma taxa de juros de 1,8% ao mês produz, ao
final de determinado período, juros no valor de R$ 27.000,00. Calcular o prazo de aplicação.
Solução:
c = R$ 250.000,00
i = 1,8% ao mês = 0,018
j = R$ 27.000,00
n=?
J=c.i.n
27.000 = 250.000 . 0,018 . n
27.000 = 4.500 n
n = 27.000 / 4.500
n = 6 meses.
II.9 – MONTANTE E CAPITAL
Um determinado capital, quando aplicado à taxa periódica de juros por determinado tempo,
produz um valor acumulado denominado de montante, e identificado em juros simples por M. Em
outras palavras, o montante é constituído do capital mais o valor acumulado dos juros, isto é:
M=c+j
(1)
J=c.i.n
(2)
No entanto, sabe-se que:
Substituindo (2) em (1), temos:
M=c+c.i.n
M = c (1 + i . n)
17
Exemplo 5.
Uma pessoa aplica R$ 18.000,00 à taxa de 1,5% ao mês, durante 8 meses. Determinar o
valor acumulado ao final do período.
Solução:
c = R$ 18.000,00
i = 1,5% ao mês = 0,015
n = 8 meses
M=?
M = c (1 + i . n)
M = 18.000 (1 + 0,015 . 8)
M = 18.000 (1 + 0,12)
M = 18.000 . 1,12
M = R$ 20.160,00.
Exemplo 6.
Uma dívida de R$ 900.000,00 irá vencer em 4 meses. O credor está oferecendo um desconto
de 7% ao mês, caso o devedor deseje antecipar o pagamento para hoje. Calcular o valor que o
devedor pagaria caso antecipasse a liquidação da dívida.
Solução:
M = R$ 900.000,00
n = 4 meses
i = 7% ao mês = 0,07
c=?
M = c (1 + i . n)
900.000 = c (1 + 0,07 . 4)
900.000 = c (1 + 0,28)
900.000 = c . 1,28
c = 900.000 / 1,28
c = R$ 703.125,00.
II.10 – TAXA EQUIVALENTE E TAXA PROPORCIONAL
Toda operação envolve dois prazos: o que se refere à taxa de juros e o de capitalização
(ocorrência) dos juros.
Por exemplo: i = 24% ao ano. Se os encargos incidirem sobre o principal somente no final de
cada ano, as taxas serão consideradas equivalentes. Portanto, as taxas de juros simples se dizem
equivalentes quando, aplicadas a um mesmo capital e pelo mesmo intervalo de tempo, produzem o
mesmo volume de juros.
Mas, em inúmeras outras operações estes prazos não são equivalentes. Os juros podem ser
capitalizados em prazo inferior ao da taxa, devendo-se, nesta situação, ser rateado com o período de
capitalização. Nesse caso, chama-se de taxa proporcional.
Por exemplo: se uma operação tiver uma taxa de juros de 18% ao ano, com a capitalização
feita mensalmente, o percentual de juros que incidirá sobre o capital a cada mês será:
Taxa Proporcional = 18% / 12 = 1,5% ao mês.
Por exemplo, em juros simples, um capital de R$ 500.000,00, se aplicado a 2,5% ao mês ou
15% ao semestre pelo prazo de um ano, produz o mesmo montante de juro. Isto é:
18
J (2,5% a.m.) = R$ 500.000,00 x 0,025 x 12 = R$ 150.000,00
J (15% a.s.) = R$ 500.000,00 x 0,15 x 2 = R$ 150.000,00
Os juros produzidos pelas duas taxas de juros são iguais, logo definidos como equivalentes.
Exemplo 7.
Calcular a taxa anual proporcional:
a) 6% ao mês;
b) 10% ao bimestre.
Solução:
a) i = 6% x 12 = 72% ao ano.
b) i = 10% x 6 = 60% ao ano.
Exemplo 8.
Calcular a taxa de juros semestral proporcional:
a) 60% ao ano;
b) 9% ao trimestre.
Solução:
a) i = 60% / 12 x 6 = 30% a.s.
b) i = 9% / 3 x 6 = 18% a.s.
Exemplo 9.
Demonstre se 36% ao ano é proporcional a 12% ao trimestre:
Solução:
12/3 = 36/12
4 ‡ 3 (portanto, falso).
Exemplo 10.
Calcular o montante de um capital de R$ 600.000,00 aplicado à taxa de 2,3% ao mês pelo
prazo de um ano e 5 meses.
Solução:
M=?
c = R$ 600.000,00
n = 1 ano e 5 meses (17 meses)
i = 2,3 ao mês (0,023)
M = c (1 + i . n)
M = 600.000 (1 + 0,023 x 17)
M = 600.000 (1 + 0,391)
M = 600.000 . 1,391
M = R$ 834.600,00
19
Exemplo 11.
Uma dívida de R$ 30.000,00 a vencer dentro de um ano é saldada 3 meses antes. Para sua
quitação antecipada, o credor concede um desconto de 15% ao ano. Apurar o valor da dívida a ser
pago antecipadamente.
Solução:
M = R$ 30.000,00
n = 3 meses
i = 15% ao ano (15% / 12 = 1,25% ao mês = 0,0125)
c=?
M = c (1 + i . n)
30.000 = c (1 + 0,0125 x 3)
30.000 = c (1 + 0,0375)
30.000 = 1,0375 c
c = 30.000 / 1,0375 = R$ 28.915,66
II.11 – JUROS EXATOS E JUROS COMERCIAIS
Os juros exatos referem-se ao calendário civil, ou seja, 365 dias. Os juros comerciais
admitem o mês com 30 dias e, portanto, o ano com 360 dias.
Por exemplo, 12% ao ano equivalem, pelos critérios enunciados, à taxa diária de:
a) juros exatos = 12% / 365 dias = 0,032877% ao dia;
b) juros comerciais = 12% / 360 dias = 0,033333% ao dia.
Portanto, o juros comerciais diários são ligeiramente superiores aos juros exatos, devido ao
menor número de dias considerado no intervalo de tempo.
II.12 – EQUIVALÊNCIA FINANCEIRA
O problema da equivalência financeira constitui-se no raciocínio básico da matemática
financeira. Conceitualmente, dois ou mais capitais representativos de certa data se dizem
equivalentes quando, a certa taxa de juros, produzem resultados iguais numa data comum.
Por exemplo, R$ 120,00 vencíveis daqui a um ano e R$ 100,00, hoje, são equivalentes a uma
taxa de juros simples de 20% ao ano, uma vez que os R$ 100,00, capitalizados, produziriam R$
120,00 dentro de um ano, ou os R$ 120,00, no final do primeiro ano, resultariam em R$ 100,00 se
atualizados para hoje.
Exemplo 12.
Determinar se R$ 438.080,00 vencíveis daqui a 8 meses é equivalente a se receber hoje R$
296.000,00, admitindo uma taxa de juros simples de 6% ao mês.
Solução:
Data focal 8 meses
M = c (1 + i . n)
M = 296.000 (1 + 0,06 x 8)
M = 296.000 (1 + 0,48)
M = 296.000 x 1,48
M = R$ 438.080,00.
Data focal 0 (hoje)
M = c (1 + i . n)
438.080 = c (1 + 0,06 x 8)
438.080 = c (1 + 0,48)
438.000 = 1,48 c
c = 438.080/1,48 = R$ 296.000,00.
20
II.13 – EXERCÍCIOS RESOLVIDOS
1. Uma pessoa aplicou em uma instituição financeira R$ 18.000,00 resgatando R$ 21.456,00,
quatro meses depois. Calcular a taxa mensal de juros simples auferida nesta aplicação.
Solução:
c = R$ 18.000,00
M = R$ 21.456,00
n = 4 meses
i=?
M = c (1 + i . n)
21.456 = 18.000 (1 + i . 4)
21.456 = 18.000 + 72.000 i
21.456 – 18.000 = 72.000 i
i = 3.456 / 72.000
i = 0,048 = 4,8% a.m.
2. Se uma pessoa necessitar de R$ 100.000,00 daqui a 10 meses, quanto deverá ela
depositar num fundo de poupança que remunera à taxa linear de 12% ao ano?
Solução:
M = R$ 100.000,00
n = 10 meses
i = 12% ao ano = 1% ao mês = 0,01
c=?
M = c (1 + i . n)
100.000 = c (1 + 0,01. 10)
100.000 = c (1 + 0,1)
100.000 = 1,1 c
c = 100.000 / 1,1
c = R$ 90.909,09
3. Determinar a taxa bimestral de juros simples que faz com que um capital triplique de valor
após 2 anos.
Solução:
M = R$ 3,00
n = 12 bimestres
i=?
c = R$ 1,00
M = c (1 + i . n)
3 = 1 (1 + i. 12)
3 = 1 + 12 i
3 - 1 + 12 i
2 = 12 i
i = 2 / 12
i = 16,7% a. b.
4. Um título com valor nominal de R$ 7.200,00 vence em 120 dias. Para uma taxa de juros
simples de 31,2% ao ano, pede-se calcular o valor deste título.
a) hoje;
b) dois meses antes do seu vencimento;
21
c) um mês após o vencimento.
Solução:
M = R$ 7.200,00
n = 4 meses
i = 31,2% ao ano = 0,312/12 = 0,026
c=?
a)
M = c (1 + i . n)
7.200 = c (1 + 0,026 x 4)
7.200 = c (1 + 0,104)
7.200 = 1,104 c
c = 7.200 / 1,104
c = R$ 6.521,74.
b)
M = c (1 + i . n)
7.200 = c (1 + 0,026 x 2)
7.200 = c (1 + 0,052)
7.200 = 1,052 c
c = 7.200 / 1,052
c = R$ 6.844,11.
c)
M = c (1 + i . n)
M = 7.200 (1 + 0,026 x 1)
M = 7.200 (1 + 0,026)
M = 7.200 + 187,20
M = R$ 7.387,20.
5. Uma pessoa deve dois títulos no valor de R$ 25.000,00 e R$ 56.000,00 cada. O primeiro
título vence de hoje a 2 meses, e o segundo um mês após. O devedor deseja propor a substituição
destas duas obrigações por um único pagamento ao final do 5° mês. Considerando 3% ao mês a taxa
corrente de juros simples, determinar o valor deste pagamento único.
Solução:
25.000 56.000
0
1
2
3
4
5 meses
c1 = R$ 25.000,00 e c2 = R$ 56.000,00
n1 = 2 meses e n2 = 3 meses
i = 3% ao mês = 0,03
M5 = ?
M = c (1 + i . n)
M5 = 25.000 (1 + 0,03 x 3) + 56.000 (1 + 0,03 x 2)
M5 = 25.000 (1 + 0,09) + 56.000 (1 + 0,06)
M5 = 25.000 x 1,09 + 56.000 x 1,06
M5 = 27.250 + 59.360
M5 = R$ 86.610,00.
6. Uma pessoa tem os seguintes compromissos financeiros:
. R$ 35.000,00 vencíveis no fim de 3 meses;
. R$ 65.000,00 vencíveis no fim de 5 meses.
Para o resgate dessas dívidas, o devedor pretende utilizar suas reservas financeiras
aplicando-as em uma conta de poupança, que rende 66% ao ano de juros simples. Pede-se
22
determinar o valor do capital que deve ser aplicado nesta poupança de forma que posam ser sacados
os valores devidos em suas respectivas datas de vencimentos.
Solução:
35.000
0
1
2
3
65.000
4
5 meses
M1 = R$ 35.000,00 e M2 = R$ 65.000,00
n1 = 3 meses e n2 = 5 meses
i = 66% ao ano = 5,5 ao mês = 0,055
c5 = ?
M = c (1 + i . n) ou c = M / (1 + i . n)
c5 = 35.000 / (1 + 0,055 x 3) + 65.000 / (1 + 0,055 x 5)
c5 = 35.000 / (1 + 0,165) + 65.000 / (1 + 0,275)
c5 = 35.000 / 1,165 + 65.000 / 1,275
c5 = 30.042,92 + 50.980,39
c5 = R$ 81.023,31
7. Uma dívida no valor de R$ 48.000,00 vence daqui a 6 meses. O devedor pretende resgatar
a dívida pagando R$ 4.800,00 hoje, R$ 14.000,00 de hoje a dois meses, e o restante um mês após a
data de vencimento. Sendo o momento deste último pagamento definido como a data focal da
operação e sabendo-se ainda que é de 34,8% ao ano a taxa linear de juros adotada nesta operação,
determinar ao montante do pagamento.
Solução:
48.000
0
4.800
1
2
14.000
3
4
5
6
7 meses
data focal
c1 = R$ 48.000,00, c2 = R$ 4.800,00 e c3 = R$ 14.000,00
n1 = 1 mês, n2 = 7 meses e n3 = 5 meses
i = 34,8% ao ano = 34,8 / 12 = 2,9% ao mês = 0,029.
MDF = ?
Daqui a 7 meses:
M = c (1 + i . n)
M6 = 48.000 (1 + 0,029 x 1)
M6 = 48.000 x 1,029
M6 = R$ 49.392,00
Hoje (R$ 4.800,00)
M = c (1 + i . n)
MHoje = 4.800 (1 + 0,029 x 7)
MHoje = 4.800 (1 + 0,203)
MHoje = 4.800 x 1,203
MHoje = R$ 5.774,40
2 meses (R$ 14.000,00)
M = c (1 + i . n)
M2 = 14.000 (1 + 0,029 x 5)
23
M2 = 14.000 (1 + 0,145)
M2 = 14.000 x 1,145
M6 = R$ 16.030,00
Dívida na Data Focal
MDF = M6 - MHoje - M2
MDF = 49.392,00 – 5.774,40 – 16.030,00
MDF = R$ 27.587,60
II.14 – EXERCÍCIOS PROPOSTOS
1. Calcular a taxa mensal proporcional de juros de:
a)
b)
c)
d)
e)
14,4% ao ano;
6,8% ao quadrimestre;
11,4% ao semestre;
110,4% ao ano;
54,72% ao biênio.
2. Calcular a taxa trimestral proporcional a juros de:
a) 120% ao ano;
b) 3,2% ao quadrimestre;
c) 1,5% ao mês.
3. Determinar a taxa de juros simples anual proporcional ás seguintes taxas:
a) 2,5% ao mês;
b) 56% ao quadrimestre;
c) 12,5% para 5 meses.
4. Calcular o montante, de R$ 85.000,00, aplicado por:
a) 7 meses à taxa linear de 2,5% ao mês;
b) 9 meses à taxa linear de 11.6% ao semestre;
c) 1 ano e 5 meses à taxa linear de 21% ao ano.
5. Determinar os juros e o montante de uma aplicação de R$ 300.000,00, por 19 meses, à
taxa linear de 42% ao ano.
6. Calcular o valor dos juros referente a uma aplicação financeira de R$ 7.500,00, que perde
15% de taxa nominal ao ano, pelo período de 2 anos e 3 meses.
7. Qual o capital que produz R$ 18.000,00 de juros simples, à taxa de 3% ao mês, pelo prazo
de:
a)
b)
c)
d)
60 dias;
80 dias;
3 meses e 20 dias;
2 anos, 4 meses e 14 dias.
8. Uma pessoas aplicou R$ 12.000,00 numa Instituição Financeira resgatando, após 7
meses, o montante de R$ 13.008,00. Qual a taxa de juros equivalente linear mensal que o aplicador
recebeu?
9. Uma nota promissória de valos nominal de R$ 140.000,00 é resgatada dois meses antes
de seu vencimento. Qual o valor pago no resgate, sabendo-se que a taxa de juros simples é de 1,9%
ao mês?
24
10. O montante de um capital de R$ 6.600,00 ao final de 7 meses é determinado
adicionando-se R$ 1.090,32 de juros. Calcular a taxa linear mensal e anual utilizada.
11. Um empréstimo de R$ 3.480,00 foi resgatado 5 meses depois pelo valor de R$ 3.949,80.
Calcular a taxa de juros simples em base mensais e anuais desta operação.
12. Se o valor atual de um título é igual a 4/5 de seu valor nominal e o prazo de aplicação for
de 15 meses, qual a taxa de juros simples considerada?
13. Uma mercadoria é oferecida num magazine por R$ 130,00 a vista, ou nas seguintes
condições: 20% de entrada e um pagamento de R$ 106,90 em 30 dias. Calcular a taxa linear mensal
de juros que está sendo cobrada.
14. Em quanto tempo um capital de R$ 4.000,00 aplicado a 29,3% ao ano pelo regime linear
renderá R$ 1.940,00?
15. Em quanto tempo duplica um capital aplicado à taxa simples de 8% ao ano?
16. Em quanto tempo triplica um capital que cresce à taxa de 21% ao semestre?
17. O valor de resgate de um título é 140% maior que o valor da aplicação. Sendo 30% ao
ano a taxa de juros simples, pede-se calcular o prazo da aplicação.
18. Uma aplicação de R$ 15.000,00 é efetuada pelo prazo de 3 meses à taxa de juros
simples de 26% ao ano. Que outra quantia deve ser aplicada por 2 meses à taxa linear de 18% ao
ano para se obter o mesmo rendimento financeiro?
19. Um TV em cores é vendida nas seguintes condições:
preço à vista = R$ 1.800,00;
condições a prazo = 30% de entrada e R$ 1.306,00 em 30 dias.
Determinar a taxa de juros simples cobrada na venda a prazo.
20. Um eletrodoméstico é vendido em três pagamentos mensais e iguais. O primeiro
pagamento é efetuado no ato da compra, e os demais são devidos em 30 e 60 dias. Sendo de 4,4%
ao mês à taxa linear de juros, pede-se calcular até que valor interessa adquirir o bem a vista.
21. Uma divida é composta de três pagamentos no valor de R$ 2.800,00, R$ 4.200,00 e R$
7.000,00, vencíveis em 60, 90 e 150 dias, respectivamente. Sabe-se ainda que a taxa de juros
simples de mercado é de 4,5% ao mês. Determinar os pagamentos:
a) hoje;
b) daqui a 7 meses.
22. Um negociante tem as seguintes obrigações de pagamento com um banco:
R$ 18.000,00 vencíveis em 37 dias;
R$ 42.000,00 vencíveis em 83 dias;
R$ 100.0000,00 vencíveis em 114 dias.
Com problemas de caixa nestas datas deseja substituir o fluxo de pagamentos pelo seguinte
esquema:
R$ 20.000,00 em 60 dias;
R$ 50.000,00 em 100 dias;
restante em 150 dias.
25
Sendo de 3,2% ao mês a taxa de juros simples adotada pelo banco nestas operações, pedese calcular o valor do pagamento remanescente adotado como data focal o momento atual.
23. Uma maquina calculadora esta sendo vendida a prazo nas seguintes condições:
R$ 128,00 de entrada;
R$ 192,00 em 30 dias;
R$ 192,00 em 60 dias.
Sendo de 1,1% ao mês a taxa linear de juros, pede-se calcular até que preço é interessante
comprar a máquina à vista.
24. Uma pessoa tem uma divida composta dos seguintes pagamentos:
R$ 22.000,00 de hoje a 2 meses;
R$ 57.000,00 de hoje a 5 meses;
R$ 90.000,00 de hoje a 7 meses.
Deseja trocar estas obrigações equivalentes por dois pagamentos iguais, vencíveis o primeiro
ao final do 6° mês e o segundo no 8° mês. Sendo de 3,7% ao mês de juros simples, calcular o valor
destes pagamentos admitindo-se o pagamento hoje.
II.15 – RESPOSTAS DOS EXERCÍCIOS PROPOSTOS DE JUROS SIMPLES:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
a) 1,2% a.m.;
b) 1,7% a.m.;
c) 1,9% a.m.;
d) 9,2% a.m.;
e) 2,28% a.m.
a) 30% a.t.;
b) 2,4% a.t.;
c) 4,5% a.t.
a) 30% a.a.;
b) 168% a.a.;
c) 30% a.a.
a) M = R$ 99.875,00
b) M = R$ 99.790,00
c) M = R$ 110.287,50
M = R$ 499.500,00
J = R$ 199.500,00
J = R$ 2.531,25
a) c = R$ 300.000,00
b) c = R$ 225.000,00
c) c = R$ 163.636,36
d) c = R$ 21.077,28
i = 1,2% a.m.
c = R$ 134.874,76.
i = 28,32% a.a.
i = 32,4% a.a.
i = 1,7% a.m.
i = 2,79% a.m.
n = Ξ 20 meses.
n = 12,5% anos
n = 57,1428 meses
n = 56 meses
c = R$ 32.500,00
i = 3,65% a.m.
% desconto = 95,9%, ou 4,1%
a) R$ 11.983,54
26
22.
23.
24.
b) R$ 16.016,00
M = R$ 94.170,19
Ctotal = R$ 505,78
Pagamentos = R$ 88.174,78
27
II.16 – JUROS COMPOSTOS
O regime de juros compostos considera que os juros formados em cada período são
acrescidos ao capital formando montante (capital mais juros) do período. Esse montante, por sua vez,
passará a render juros no período seguinte formando um novo montante (constituído do capital inicial,
dos juros acumulados e dos juros sobre juros formados em períodos anteriores), e assim por diante.
Em síntese: os juros são compostos quando, a cada período, eles são incorporados ao
capital e o novo capital passa também a render juros.
II.17 – FÓRMULAS DE JUROS COMPOSTOS
Com juros compostos, no final de cada período, o juro é incorporado ao principal ou capital,
passando assim a também render juros no próximo período. Podemos deduzir a expressão da
seguinte maneira:
• No primeiro período:
M1 = c + c . i = c . (1 + i)
• No segundo período:
M2 = M1 + M1. i = M1 . (1 + i) = c. (1 + i).(1 + i) = c. (1 + i)
2
• No terceiro período:
M3 = M2 + M2.i = M2 . (1 + i) = c . (1 + i)2. (1 + i) = c. (1 + i)
3
Se generalizarmos para um número de períodos igual a n, tem-se a expressão geral para
cálculo de juros compostos, dada por:
M = c (1 + i)n
onde: M = montante, c = capital, i = taxa de juros e n = número de períodos que o capital C
(capital inicial) foi aplicado.
Exemplos:
1. Se uma pessoa deseja obter R$ 27.500,00 dentro de um ano, quanto deverá ela depositar
hoje numa alternativa de poupança, que rende 1,7% de juros compostos ao mês?
Solução:
M = R$ 27.500,00
n = 1 ano = 12 meses
i = 1,7% a.m. = 0,017
c=?
M = c (1 + i)n
12
27.500 = c (1 + 0,017)
12
27.500 = c (1,017)
12
27.500 = c (1,017)
27.500 = 1,2242 c
c = 27.500 / 1,2242 = R$ 22.463,65
2. Qual o valor de resgate de uma aplicação de R$ 12.000,00 em um título pelo prazo de 8
meses, à taxa de juros composta de 3,5% a.m.?
28
Solução:
M=?
c = R$ 12.000,00
n = 8 meses
i = 3,5% a.m. = 0,035
M = c (1 + i)n
8
M = 12.000 (1 + 0,035)
8
M = 12.000 (1,035)
M = R$ 15.801,60
3. Determinar a taxa mensal composta de juros de uma aplicação de R$ 40.000,00 que
produz um montante de R$ 43.894,63 ao final de um quadrimestre.
Solução:
i = ?% a.m.
c = R$ 40.000,00
M = R$ 43.894,63
n = 4 meses
M = c (1 + i)n
43.894,63 = 40.000 (1 + i) 4
43.894,63 / 40.000 = (1 + i) 4
1,0974 = (1 + i) 4
1,09741/4 = 1 + i
1,0235 = 1 + i
1,0235 – 1 = i
0,0235 = i
i = 2,35% a.m.
4. Uma aplicação de R$ 22.000,00, efetuada em certa data produz, à taxa composta de juros
de 2,4% ao mês, um montante de R$ 26.596,40 em certa data futura. Calcular o prazo da operação.
Solução:
c = R$ 22.000,00
M = R$ 26.596,40
i = 2,4% a.m. = 0,024
n = ? meses
M = c (1 + i)n
26.596,40 = 22.000 (1 + 0,024)n
26.596,40 / 22.000 = (1,024)n
1,2089 = (1,024)n
n = log 1,2089 / log 1,024
n = 0,0824 / 0,0103
n = 8 meses
5. Determinar os juros pagos de um empréstimo de R$ 88.000,00 pelo prazo de 5 meses à
taxa composta de 4,5% ao mês.
Solução:
J=?
29
c = R$ 88.000,00
M = R$ ?
i = 4,5% a.m. = 0,045
n = 5 meses
M = c (1 + i)n
M = 88.000 (1 + 0,045i)5
M = 88.000 (1,045)5
M = 88.000 x 1,2462
M = R$ 109.665,60
J=M–C
J = 109.665,60 – 88.000
J = R$ 21.665,60
II.18 – TAXAS EQUIVALENTES
Já sabemos que duas taxas são equivalentes quando aplicadas a um mesmo capital, durante
o mesmo período de tempo, produzem o mesmo rendimento.
Na capitalização simples, duas taxas proporcionais são também equivalentes.
capitalização composta, não.
Na
No regime de juros compostos, uma aplicação que paga 10% a.m. representa o rendimento,
em um trimestre, de:
Atribuindo um capital R$ 100, temos:
3
M = 100(1,1) equivale a M = 10 x 1,331 equivale a M = R$ 133,10.
Portanto, o rendimento no trimestre foi de 33,1%.
Logo, 10% ao mês são equivalentes a 33,1% ao trimestre. Ambas podem ser utilizadas nos
problemas; são efetivas.
Podemos generalizar o cálculo da equivalência entre taxas assim:
Equivalência entre ANO e MÊS: (1 + ia) = (1 + im)
12
Equivalência entre ANO e TRIMESTRE: (1 + ia) = (1 + it)
4
6
Equivalência entre SEMESTRE e MÊS: (1 + im) = (1 + is)
Exemplos
1. Quais as taxas de juros compostos mensal e trimestral equivalentes a 25% ao ano?
Solução:
Observamos que 25% ao ano é uma taxa nominal; a capitalização é mensal.
a) mensal
ANO e MÊS: (1 + ia) = (1 + im)
12
(1 + 0,25) = (1 + im)
12
√1,25 = 1 + im
1,01877 – 1 = im
im = 0,01877 = 1,877% a.m.
12
30
b) trimestral
ANO e MÊS: (1 + ia) = (1 + it)
4
(1 + 0,25) = (1 + it)
4
√1,25 = 1 + it
1,05737 – 1 = it
it = 0,05737 = 5,737% a.t.
4
2. Explicar a melhor opção: aplicar um capital de R$ 60.000,00 à taxa de juros compostos de
9,9% ao semestre ou à taxa de 20,78% ao ano.
a) 9,9% ao semestre
n
M = c (1 + i)
2
M = 60.000 (1 + 0,099)
2
M = 60.000 (1,099)
M = 60.000 x 1,2078
M = R$ 72.468,00
b) 20,78% ao ano
n
M = c (1 + i)
1
M = 60.000 (1 + 0,2078)
1
M = 60.000 (1,2078)
M = 60.000 x 1,2078
M = R$ 72.468,00
Portanto, as taxas são equivalentes, pois produzem resultados iguais para um mesmo
período.
3. Demonstrar se a taxa de juros compostos de 11,8387% ao trimestre é equivalente à taxa
de 20,4999% para cinco meses. Calcular também a equivalência mensal composta dessas taxas.
TRIMESTRE e MÊS
(1 + it) = (1 + im)
(1 + 0,118387) = (1 + im)
3
5 MESES e MÊS
3
5
(1 + im) = (1 + 0,204999)
3
5
(1 + im) = 1,204999
5
√1,118387 = 1 + im
(1 + im) = √1,204999
1,0380 – 1 = im
(1 + im) = 1,0380
0,0380 = im
Im = 1,0380 – 1
im = 3,8%
Im = 0,0380
im = 3,8%
Portanto, as taxas são equivalentes.
II.19 – EXERCÍCIOS PROPOSTOS
1. Um capital de R$ 200.000,00 é aplicado a juros compostos de 10% ao ano. Calcule o
montante após 4 anos.
2. Joana aplicou R$ 400,00 num investimento que rende 2% a.m., a juros compostos. Qual o
montante após 1 ano?
3. Calcular o montante, ao final de um ano de aplicação, de um capital de R$ 600,00, à taxa
composta de 4% ao mês.
31
4. O capital R$ 500,00 foi aplicado durante 8 meses à taxa de 5% ao mês. Qual o valor dos
juros compostos produzidos?
5. Qual a aplicação inicial que, empregada por 1 ano e seis meses, à taxa de juros compostos
de 3% ao trimestre, se torna igual a R$ 477,62?
6. Quais as taxas de juros compostos mensal e trimestral equivalentes a 25% ao ano?
7. Explicar a melhor opção: aplicar um capital de R$ 60.000,00 à taxa de juros compostos de
9,9% ao semestre ou à taxa de 20,78% ao ano.
8. Demonstrar se a taxa de juros compostos de 11,8387% ao trimestre é equivalente à taxa
de 20,4999% para cinco meses. Calcular também a equivalência mensal composta dessas taxas.
9. Um capital de R$ 2.500,00 esteve aplicado à taxa mensal de 2%, num regime de
capitalização composta. Após um período de 2 meses, os juros resultantes dessa aplicação serão
maiores que R$ 100,00. Certo ou Errado? Demonstre.
10. A taxa de juros compostos de 2% ao mês é proporcional à de 25% ao ano. Certo ou
Errado? Demonstre.
11. Paguei de juros um total de R$ 9.852,00 por um empréstimo de 18 meses a uma taxa de
juro composto de 2,25% a.m. O capital tomado no emprestado foi igual a R$ 20.000,00. Certo ou
Errado? Demonstre.
12. A taxa efetiva semestral de 97,38% é equivalente à taxa mensal de 11%. Certo ou
Errado? Demonstre.
13. Resgata-se um título por R$ 4.862,00, com 4 meses de antecedência. O valor nominal do
título, sendo a taxa de 60% ao ano com capitalização mensal, e o critério do desconto racional
composto, é igual a R$ 4.000,00. Certo ou Errado? Demonstre.
14 - Um título de R$ 8.651,50 é descontado 3 meses antes do vencimento, à taxa racional
composta de 10% ao mês. O valor atual é igual a R$ 6.500,00. Certo ou Errado? Demonstre.
15. Um capital, após 5 anos de investimento, à taxa de 12% ao ano, capitalizada
semestralmente, eleva-se a R$ 5.820,10. O valor desse capital é superior a R$ 3.500,00. Certo ou
Errado? Demonstre.
16. O pagamento de um empréstimo, que seria quitado em uma única prestação de R$
26.000,00 ao final do segundo ano, com uma taxa de juros de 2% a.m., for antecipado para o final do
primeiro ano, o valor a ser pago será superior a R$ 19.800,00. Certo ou Errado? Demonstre.
17. Considerando que o regime praticado é o de juros compostos, à taxa mensal de 2%, caso
o saldo devedor de um empréstimo seja hoje de R$ 30.000,00, se nenhum pagamento for efetuado,
esse valor será superior a R$ 39.000,00, ao final do período de um ano. Certo ou Errado? Demonstre.
18. Demonstre porque uma aplicação efetuada durante 01 (um) mês, à mesma taxa, tem o
rendimento igual tanto para juros simples como para juros compostos.
19. A taxa de juros compostos de 2% ao mês é proporcional à de 24% ao ano. Certo ou
Errado? Demonstre.
20. A taxa efetiva semestral de 97,38% é equivalente à taxa mensal de 12%. Certo ou
Errado? Demonstre.
21. Na taxa equivalente, utiliza-se o regime de juros simples e, na taxa proporcional, o regime
de juros compostos. Certo ou Errado.
32
22. Aplicando-se R$ 15.000,00, a uma taxa de juros compostos de 1,7% a.m., quanto se
receberá de volta após um ano de aplicação? Quanto foram os juros obtidos?
23. Pagou-se de juros um total R$ 2.447,22 por um empréstimo de 8 meses a uma taxa de
juros compostos de 1,4% a.m. Quanto foi o capital emprestado?
24. Planeja-se emprestar R$ 18.000,00 por um período de 18 meses ao final do qual se
pretende receber de volta R$ 26.866,57. Quanto deve ser a taxa de juros compostos para que se
venha conseguir este montante?
25. Precisa-se aplicar R$ 100.000,00 por um período de quantos meses, a uma taxa de juros
compostos de 0,5% a.m., para que ao final da aplicação se obtenha o dobro deste capital?
26. R$ 10.000,00 aplicados por 6 meses a uma taxa de juros simples de 3% a.m., para
produzir o mesmo montante na modalidade de juros compostos em um aplicação com a mesma
duração, precisará ser aplicada a qual taxa mensal?
27. O valor final de um empréstimo de R$ 5.000,00 por um período de 7 meses é R$
5.862,72. Qual a taxa de juros da aplicação?
28. Alguém toma R$ 100.000,00 emprestados, a uma taxa de juros compostos de 1% a.m.,
qual é o valor total que deverá ser pago após 100 meses?
II.20 – RESPOSTAS DOS EXERCÍCIOS PROPOSTOS DE JUROS COMPOSTOS:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
M = R$ 292.820,00
M = R$ 507,29
M = R$ 960,60
J = R$ 238,75
c = R$ 400,00
a) im = 1,877% a.m.
b) it = 5,737% a.t.
M = R$ 72.468,00. Portanto, as taxas são equivalentes.
im = 3,8%. Portanto, as taxas são equivalentes.
J = R$ 101,00. Portanto, certo.
1,88% ≠ 2,00% ou 26,82% ≠ 25,00%. Portanto, errado.
c = R$ 20.000,00. Portanto, certo.
im = 12%. Portanto, errado.
c = R$ 4.157,02. Portanto, errado.
c = R$ 6.500,00. Portanto, certo.
c = R$ 3.250,00. Portanto, errado.
c = R$ 20.501,50. Portanto, certo.
M = R$ 38.046,00. Portanto, errado.
M = R$ 110,00, para c = R$ 100,00 e i = 10% a.m.
ia = 26,82% a.a. Portanto, errado.
ia = 97,38% a.s. Portanto, certo.
Errado.
J = R$ 3.363,00
c = R$ 20.809,70
i = 2,25% a.m.
n = aproximadamente 137 meses.
i = 2,8% a.m.
i = 2,3% a.m.
J = R$ 170.480,00.
33
BIBLIOGRAFIA
1. BUARQUE, Cristovam. Avaliação Econômica de Projetos. Rio de Janeiro: Campus, 1984.
2. BRANCO, Anísio Costa Castelo. Matemática Financeira Aplicada. São Paulo: ThomsonPioneira, 2002.
3. CASAROTTO FILHO, Nelson, KOPITTKE, Bruno H. Análise de Investimentos. São Paulo:
Atlas, 2000.
4. DE FARO. Clóvis. Matemática Financeira. São Paulo: Atlas, 1982.
5. EHRLICH, Pierre J. Engenharia Econômica. São Paulo: Atlas, 1983.
6. FERREIRA, Roberto G. Engenharia Econômica e Avaliação de Projetos de Investimento.
São Paulo: Atlas, 2009.
7. FLEISCHER, Gerald A. Teoria da Aplicação do Capital. São Paulo: Edgard Blucher, 1973.
8. GITMAN, Lawrence J. Princípios de Administração Financeira, São Paulo: Harbra, 2002.
9. GOUVEIA, Nelson. Contabilidade. 2° ed. São Paulo: McGraw-Hill, 1982.
10. HAZZAN, Samuel; POMPEO, José Nicolau. Matemática Financeira. São Paulo: Saraiva, 2004.
11. HIRSCHFELD, Henrique. Engenharia Econômica e Análise de Custos. São Paulo: Atlas, 1992.
12. HOJI, Masakazu. Administração Financeira: uma abordagem pratica. São Paulo: Atlas, 2006.
13. NEVES, César das. Análise de Investimentos. Rio de Janeiro: Zahar, 1982.
14. NETO, Alexandre Assaf. Matemática Financeira e Suas Aplicações. São Paulo: Atlas, 2006.
15. OLIVEIRA, J. A. Nascimento. Engenharia Econômica: uma abordagem às decisões de
investimento. São Paulo: McGraw-Hill, 1982.
16. SAMANEZ, Carlos Patrício. Matemática Financeira – Aplicações à Análise de Investimentos.
São Paulo: Prentice Hall, 2002.
17. WALTER, Milton A. e BRAGA, Hugo R. Demonstrações Financeiras: um enfoque gerencial.
São Paulo: Saraiva, 1981.
18. WOILER, S. et alli. Projetos. São Paulo: Atlas, 1983.
34