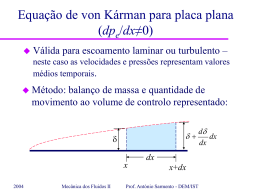
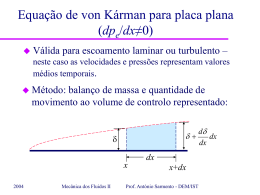
MECÂNICA DOS FLUIDOS II

Matéria:
–
–
–
–

Escoamentos laminares e turbulentos: filmes
Campo médio e flutuação turbulenta
Difusão molecular e difusão turbulenta;
Distribuição de tensão de corte num escoamento turbulento
num tubo.
Bibliografia:
– Sabersky – Fluid Flow: 7.1, 7.2;
– White – Fluid Mechanics: 6.1.
2004
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Filmes: sequências do mfm
– Boundary Layers/Instability, Transition and Trubulence:
» Instability and transition in pipe and duct flows;
» Turbulent mixing and diffusion;
– Kinematics/Timelines/Timelines in turbulent flows

2004
e filme 135
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Escoamento laminar:
– Estacionário no sentido restrito (não há flutuações de
velocidade ou de pressão, p. ex.);
– Difusão apenas molecular;
– O escoamento desenvolve-se “em lâminas”.
u  U max
2004
Prof. António Sarmento - DEM/IST
y
h
MECÂNICA DOS FLUIDOS II

Escoamento turbulento:
velocidade
– Não-estacionário (há flutuações aleatórias de velocidade,
pressão, etc. em torno do valor médio);
u
u
tempo
2004
Prof. António Sarmento - DEM/IST
ut   u  ut 
MECÂNICA DOS FLUIDOS II

Escoamento turbulento:
– A turbulência é tridimensional e aleatória;
– Origem da turbulência: forças de inércia excessivas geram
instabilidades não amortecidas pela difusão molecular que
crescem e tomam a forma de vórtices turbulentos.
– Ocorre para números de Reynolds elevados:
Re 
2004
forças inércias
forças viscosas
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Escoamento turbulento:
– Vórtices turbulentos sobrepõem-se ao escoamento médio;
– Os períodos de oscilação das flutuações estão relacionados
com a dimensão dos vórtices através de t  l u
– Difusão turbulenta (normalmente dominante) com grande
capacidade de mistura, induzida pelos vórtices de maior
dimensão;
– A dissipação de energia está associada aos vórtices de
menor dimensão.
2004
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II
Perfis de velocidade num tubo
Laminar
Turbulento
1,2
u(r)/Umax
1
0,8
 u 
 
 r  r  R
  r 2 
u r   U max 1    
  R  
0,6
0,4
0,2
0
0
2004
0,25
0,5
r/R
0,75
Prof. António Sarmento - DEM/IST
1
 0lam   0turb
MECÂNICA DOS FLUIDOS II
 Distribuição
da tensão de corte (laminar ou turbulento):
r0

r
l
p

p+p
p
u r 
- Escoamento completamente desenvolvido:
0
0
x
r
- Balanço de quantidade de movimento axial:
pr  2rl
2
2004
p 2

   const .
l
r
Prof. António Sarmento - DEM/IST

r

 0 r0
Variação linear
MECÂNICA DOS FLUIDOS II
2
 p   0l
r0

Queda de pressão:

Factor de atrito:

Diagrama de Moody:
4 0
f 1
2

V
2
Redução de f com Re
64
Re
Ln f
Turbulento
Aumento de f com a
passagem a turbulento
2100
2004
(Laminar)
Prof. António Sarmento - DEM/IST
Ln Re
MECÂNICA DOS FLUIDOS II

Difusão turbulenta transversal de quantidade de
movimento longitudinal:
– Elementos centrais cedem quantidade de movimento
longitudinal aos periféricos
Devido a trocas constantes de massas de fluido que viajam a
velocidades diferentes promovidas por vórtices turbulentos
2004
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Tensão de corte total:
du
du
 
 T
dy
dy
Viscosidade molecular
Depende apenas do fluido
Viscosidade turbulenta
(Eddy viscosity)
Depende do escoamento
Junto à parede:
T  0 Dimensão e intensidade dos vórtices limitadas
pela presença da parede

2004
Não é alterado => a amplitude do movimento
das moléculas não é afectada pela parede
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Tensão de corte total:
Viscosidade molecular
du
du
 
 T
dy
dy
Viscosidade turbulenta
Junto à parede:
T  0 Dimensão e intensidade dos vórtices limitadas
pela presença da parede

Não é alterado => a amplitude do movimento
das moléculas não é afectada pela parede
Existe sempre uma SUB-CAMADA LAMINAR (viscous layer)
junto à parede:  não alterado e du dy intenso.
2004
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Regiões num tubo:
• Sub-camada laminar junto à parede (sem turbulência);
• Região central: turbulência dominante (difusão/tensão
viscosa desprezável), turbulência isotrópica, flutuações
não-correlacionadas;
• Região intermédia (transition region ou buffer layer):
difusão molecular e turbulenta igualmente importantes,
turbulência anisotrópica, flutuações correlacionadas.
Filme 02 e sequência Fully Turbulent Duct Flow
2004
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II
 Tubos
(superfícies) hidraulicamente lisos:
• Rugosidade do tubo inferior à espessura da sub-camada
laminar – o escoamento comporta-se como num tubo liso.
2004
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II
Fluid Flow 7.24
Para
Re<105
num tubo de secção circular
=1,2 kg/m3,  = 1,8 x 10-5 Pa.s
tubo hidraulicamente liso
d = 0,15 m de diâmetro, V = 8 m/s.
u
u max
 r0  r 

 
 r0 
1/ 7
a) Determine a tensão de corte deste escoamento em r/r0=0,95.
b) Que proporção desta tensão de corte é devida à viscosidade e que
proporção é devida às flutuações turbulentas?
R: a)
Re=8 x 104
Tubo liso
2004
f=0,018
 0  0,1728Pa
Prof. António Sarmento - DEM/IST
  0,1662Pa
MECÂNICA DOS FLUIDOS II
u
Para Re<105 num tubo de secção circular
R: b)
 lam
umax  r 
u
1  
 

r
7r0  r0 
 lam r 0,95r
u max
5
0
r0
 44,7 10 umax  0,0044Pa
q  r V  2  u rdr
2
0
0
2004
6

7
 r0  r 

 
 r0 
1/ 7
u max 
 lam
 2,68%
T
Prof. António Sarmento - DEM/IST
V
7 7 
2  
 8 15 
 9,8 m/s
MECÂNICA DOS FLUIDOS II
 Conceitos:
–
–
–
–
Campo médio e flutuação turbulenta
Difusão laminar e difusão turbulenta
Viscosidade molecular e Viscosidade turbulenta;
Perfil transversal da tensão de corte num escoamento
turbulento num tubo
– Sub-camada laminar; Região central; Região intermédia;
– Tubo hidraulicamente liso
 Bibliografia:
– Sabersky – Fluid Flow: 7.1, 7.2;
– White – Fluid Mechanics: 6.1.
2004
Prof. António Sarmento - DEM/IST